Sortieren auf zweidimensionalen Prozessorfeldern
Sortieren auf zweidimensionalen Prozessorfeldern
Das Sortiernetz Odd-even Transposition Sort lässt sich sehr gut auf einem eindimensionalen Prozessorfeld implementieren. Dabei hält jeder Prozessor ein Datenelement. Ein Vergleichs-Austausch-Schritt wird realisiert, indem jeweils zwei benachbarte Prozessoren ihr eigenes Datenelement mit dem des Nachbarn vergleichen und gegebenenfalls vertauschen. Bild 1 zeigt einen Odd- und einen Even-Schritt von Odd-even Transposition Sort auf einem eindimensionalen Prozessorfeld.
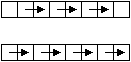
Bild 1: Sortierschritte auf einem eindimensionalen Prozessorfeld
In Prozessorfeldern können nur benachbarte Prozessoren miteinander kommunizieren. Dies gilt auch für zweidimensionale Prozessorfelder, hier hat jeder Prozessor allerdings noch zwei weitere Nachbarn in senkrechter Richtung. Bild 2 zeigt zwei mögliche Sortierschritte auf einem zweidimensionalen Prozessorfeld.
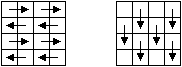
Bild 2: Sortierschritte auf einem zweidimensionalen Prozessorfeld
Problem
Die Definition des Sortierproblems wird zunächst verallgemeinert, damit nicht nur eindimensionale Datenfelder, sondern auch zweidimensionale (und darüber hinaus beliebige) Datenfelder behandelt werden können.
Definition: Sei A eine Menge von Daten mit einer Ordnungsrelation ≤. Ein Datensatz ist eine Abbildung a : J → A, wobei J eine endliche Indexmenge ist. Die Schreibweise für einen Datensatz a ist auch (ai)i ∈ J .
Beispiel: Eine Datenfolge ist ein Datensatz mit der Indexmenge
J = {0, ..., n-1}.
Ein n×n-Feld von Daten ist ein Datensatz mit der Indexmenge
J = {0, ..., n-1} × {0, ..., n-1}.
Definition: Eine Sortierrichtung ist eine bijektive Abbildung
r : J → {0, ..., |J|-1}.
Beispiel: Bei Datenfolgen entspricht r(i) = i aufsteigender Sortierrichtung, r(i) = n – 1 – i absteigender Sortierrichtung.
Bei n×n-Datenfeldern sind folgende Sortierrichtungen üblich:
| zeilenweise: | r(i, j) = i·n + j | ||||||||
| in Schlangenlinie: |
|
Definition: Das Sortierproblem besteht darin, einen beliebigen Datensatz (ai)i ∈ J so zu einem Datensatz (aφ(i))i ∈ J umzuordnen, dass gilt
∀ i, j ∈ J : aφ(i) ≤ aφ(j) für r(i) < r(j).
φ ist hierbei eine Permutation der Indexmenge J.
Die n×n-Datenfelder sollen auf einem n×n-Prozessorfeld sortiert werden. Die Daten sind den Prozessoren in natürlicher Weise so zugeordnet, dass jeder Prozessor (i, j) das Datenelement ai, j enthält. Die Sortierrichtung soll stets zeilenweise aufsteigend sein.
Untere Schranken
Befindet sich das kleinste Element anfangs in der rechten unteren Ecke des n×n-Feldes, so benötigt es mindestens 2n – 2 Schritte, um in die linke obere Ecke zu kommen. Diese triviale untere Schranke wurde von Kunde auf 3n –  2n – 3 Schritte verbessert [Kun 87].
2n – 3 Schritte verbessert [Kun 87].
In Bild 3 ist ein n×n-Feld dargestellt. Das eingezeichnete rechte untere Dreieck des Feldes wird Jokerzone genannt, da die Daten in dieser Zone zunächst noch nicht festgelegt werden. Außerhalb der Jokerzone ist das Feld mit lauter verschiedenen Daten belegt.
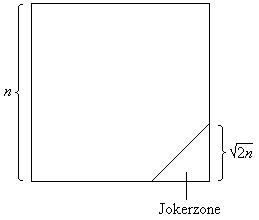
Bild 3: n×n-Feld mit Jokerzone
Die Datenelemente der Jokerzone können frühestens nach 2n –  2n – 2 Schritten die linke obere Ecke des Feldes erreichen. Das Element x, das zu diesem Zeitpunkt in der linken oberen Ecke steht, ist also unabhängig von den Daten der Jokerzone: ganz gleich, welche Werte die Daten der Jokerzone haben, wird nach 2n –
2n – 2 Schritten die linke obere Ecke des Feldes erreichen. Das Element x, das zu diesem Zeitpunkt in der linken oberen Ecke steht, ist also unabhängig von den Daten der Jokerzone: ganz gleich, welche Werte die Daten der Jokerzone haben, wird nach 2n –  2n – 2 Schritten stets dasselbe Element x in der linken oberen Ecke stehen.
2n – 2 Schritten stets dasselbe Element x in der linken oberen Ecke stehen.
Die Werte der Datenelemente der Jokerzone werden nun so gewählt, dass das Element x in der sortierten Reihenfolge an den rechten Rand des Feldes gehört. Da die Jokerzone n Elemente enthält, ist genug "Manövriermasse" vorhanden, um x an den rechten Rand zu drängen. Das Element x muss also nach dem 2n –  2n – 2-ten Schritt noch einen Weg der Länge n-1 zurücklegen, sodass insgesamt mindestens 3n –
2n – 2-ten Schritt noch einen Weg der Länge n-1 zurücklegen, sodass insgesamt mindestens 3n –  2n – 3 Schritte erforderlich sind, um das Feld zu sortieren.
2n – 3 Schritte erforderlich sind, um das Feld zu sortieren.
Sortierverfahren auf n×n-Prozessorfeldern
Bereits 1977 veröffentlichten Thompson und Kung eine Arbeit über das Sortieren auf einem n×n-Prozessorfeld [TK 77]. Der dort vorgestellte Algorithmus s2-way Mergesort war sowohl asymptotisch als auch hinsichtlich der Konstanten vor dem Term höchster Ordnung bereits optimal. Die Komplexität des Algorithmus beträgt 3n + O(n2/3 log(n)) Vergleichs-Austausch-Operationen.
Danach erschien noch eine ganze Reihe weiterer Arbeiten, in denen Sortierverfahren für n×n-Prozessorfelder mit der Zeitkomplexität O(n) vorgestellt wurden (u.a. [LSSS 85], [SchSh 86], [MG 88]). Diese Verfahren sind teilweise einfacher als das Verfahren von Thompson-Kung, jedoch alle langsamer. Lediglich der Algorithmus 3n-Sort von Schnorr und Shamir [SchSh 86] erreicht mit 3n + O(n3/4) Schritten dieselbe Konstante vor dem Term höchster Ordnung.
Als besonders einfache und gut zu implementierende Verfahren sollen im Folgenden zunächst die Verfahren LS3-Sort von Lang, Schimmler, Schmeck und Schröder [LSSS 85] sowie 4-way Mergesort von Schimmler [Schi 87] angegeben werden, ferner das ideenreiche, aber etwas langsamere Verfahren Rotatesort von Marberg und Gafni [MG 88].
Literatur
[Kun 87] M. Kunde: Lower Bounds for Sorting on Mesh-Connected Architectures. Acta Informatica 24, 121-130 (1987)
[LSSS 85] H.W. Lang, M. Schimmler, H. Schmeck, H. Schröder: Systolic Sorting on a Mesh-Connected Network. IEEE Transactions on Computers C-34, 7, 652-658 (1985)
[MG 88] J.M. Marberg, E. Gafni: Sorting in Constant Number of Row and Column Phases on a Mesh. Algorithmica 3, 561-572 (1988)
[Schi 87] M. Schimmler: Fast Sorting on the Instruction Systolic Array. Bericht Nr. 8709, Institut für Informatik, Christian-Albrechts-Universität Kiel (1987)
[SchSh 86] C.P. Schnorr, A. Shamir: An Optimal Sorting Algorithm for Mesh-Connected Computers. Proc. of the 18th ACM Symposium on Theory of Computing, 255-261 (1986)
[TK 77] C.D. Thompson, H.T. Kung: Sorting on a Mesh-Connected Parallel Computer. Communications of the ACM, 20, 4, 263-271 (1977)
[Lan 12] H.W. Lang: Algorithmen in Java. 3. Auflage, Oldenbourg (2012)
Die parallelen Sortierverfahren LS3-Sort, Rotatesort und 3n-Sort finden Sie auch in meinem Buch über Algorithmen.
Weitere Themen des Buches: Sortieren, Textsuche, Parsen und Übersetzen, Graphenalgorithmen, Arithmetik, Codierung, Kryptografie.
Themen des Buches: Sortieren, Textsuche, Parsen und Übersetzen, Graphenalgorithmen, Arithmetik, Codierung, Kryptografie.
Weiter mit: [Sortierverfahren LS3-Sort] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 01.03.1997 Updated: 07.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden

