Sortieren auf zweidimensionalen Prozessorfeldern
Sortierverfahren von Thompson-Kung
Das Verfahren von Thompson und Kung [TK 77] für das Sortieren auf zweidimensionalen Prozessorfeldern ist nicht nur asymptotisch, sondern auch hinsichtlich seiner Konstanten optimal.
Idee
Der Algorithmus Odd-even Merge [Bat 68] wird auf zweidimensionale Felder angewendet. Durch die Operation unshuffle werden die Elemente an geraden Positionen und die Elemente an ungeraden Positionen getrennt, jeweils für sich sortiert und durch die Operation shuffle wieder zusammengeführt.
Es werden drei Varianten von Algorithmen auf Grundlage dieser Idee entwickelt. Ausgangssituation ist jeweils ein k×m-Feld, das aus 2, aus 2s bzw. aus s2 in Schlangenlinie sortierten Teilfeldern besteht. Die Korrektheit der Verfahren wird mit Hilfe des 0-1-Prinzips gezeigt. Es wird daher von einer Belegung der Felder mit Nullen (weiß) und Einsen (grau) ausgegangen (Bild 1).
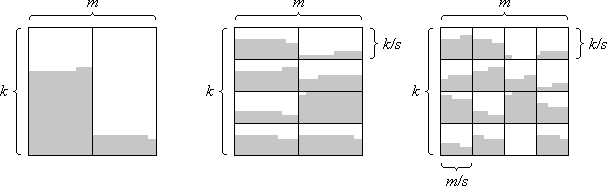
Bild 1: Ausgangssitutation für die Algorithmen 2-way-merge, 2s-way-merge und s2-way-merge
Grundoperationen
Die Algorithmen greifen auf die Grundoperationen shuffle, unshuffle, oddexchange und oets zurück.
shuffle
Ein professioneller Kartenspieler mischt einen Stoß Spielkarten, indem er die erste und die zweite Hälfte reißverschlussartig ineinander gleiten lässt. Die englische Bezeichnung hierfür ist perfect shuffle oder kurz shuffle. Sie steht für folgende Permutation, hier dargestellt für n = 8 Elemente:
| 0 1 2 3 4 5 6 7 |
| 0 4 1 5 2 6 3 7 |
Auf Prozessorfeldern kann die Permutation shuffle durch ein "Dreieck" von Vertauschungen zwischen Nachbarelementen hergestellt werden:
| 0 1 2 3 4 5 6 7 |
| ⟷ |
| ⟷ ⟷ |
| ⟷ ⟷ ⟷ |
| 0 4 1 5 2 6 3 7 |
unshuffle
Die Permutation unshuffle ist die inverse Permutation von shuffle:
| 0 1 2 3 4 5 6 7 |
| 0 2 4 6 1 3 5 7 |
Die Permutation unshuffle entsteht, wenn Spielkarten reihum an zwei Spieler verteilt werden. Der erste Spieler erhält die "geraden" Spielkarten, d.h. die Karten 0, 2, 4, 6 usw.; der zweite Spieler erhält die "ungeraden" Spielkarten, d.h. 1, 3, 5, 7 usw.
Auch die Permutation unshuffle kann auf Prozessorfeldern durch ein Dreieck von Vertauschungen zwischen Nachbarelementen hergestellt werden:
| 0 1 2 3 4 5 6 7 |
| ⟷ ⟷ ⟷ |
| ⟷ ⟷ |
| ⟷ |
| 0 2 4 6 1 3 5 7 |
oddexchange
Die Operation oddexchange wird auf ein zweidimensionales k × m-Feld angewandt. Sie bewirkt eine Vertauschung aller Elemente an den Positionen (i, j), wobei i ungerade und j gerade, mit den entsprechenden rechten Nachbarelementen (i, j+1) (i ∈ {0, ..., k-1}, j ∈ {0, ..., m-1}).
Ist die Sortierrichtung auf dem zweidimensionalen Feld die Schlangenlinie, so kommen hierdurch alle Elemente der Folge, die sich an den geraden Positionen der Sortierreihenfolge befinden ("gerade Elemente"), in eine Spalte mit geradem Spaltenindex ("gerade Spalte"), entsprechendes gilt für die ungeraden Elemente (Bild 2).
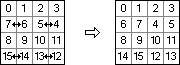
Bild 2: Operation oddexchange
oets
Die Operation oets steht für einen Schritt von Odd-even Transposition Sort. Bei einem Even-Schritt werden alle geraden Elemente mit ihren rechten Nachbarelementen verglichen und gegebenenfalls vertauscht, bei einem Odd-Schritt alle ungeraden Elemente. Odd- und Even-Schritte werden abwechselnd angewendet.
2-way-merge
Der folgende Algorithmus 2-way-merge ist zunächst die einfachste Implementation für ein k × m-Feld, wobei k, m Zweierpotenzen sind.
Prozedur 2-way-merge(k, m)
Eingabe:
k × m-Feld (m > 1), dessen linke und rechte Hälfte jeweils in Schlangenlinie sortiert ist (Bild 1a)
Ausgabe:
das in Schlangenlinie sortierte k × m-Feld
Methode:
- wenn m > 2 dann
- oddexchange
- unshuffle in den Zeilen
- 2-way-merge(k, m/2) rekursiv auf linke und rechte Hälfte anwenden
- shuffle in den Zeilen
- oddexchange
- 2 oets-Schritte auf der Schlangenlinie
- sonst
- 2-column-merge(k)
Die Rekursion bricht ab, wenn jeweils nur noch zwei Spalten zu verschmelzen sind. Dann wird das folgende Verfahren 2-column-merge verwendet.
Prozedur 2-column-merge(k)
Eingabe:
k × 2-Feld, dessen linke und rechte Spalte sortiert ist
Ausgabe:
das in Schlangenlinie sortierte k × 2-Feld
Methode:
- oddexchange
- Sortieren der Spalten
- 2 oets-Schritte auf der Schlangenlinie
Korrektheit von 2-way-merge
Nach dem 0-1-Prinzip kann von einer Belegung des Feldes mit Nullen und Einsen ausgegangen werden.
1. Fall: m > 2
Durch Schritt 1 kommen alle geraden Elemente der Sortierreihenfolge in eine gerade Spalte, alle ungeraden Elemente in eine ungerade Spalte.
In jeder der beiden Hälften des Feldes können dadurch die ungeraden Spalten zusammengenommen eine Eins mehr enthalten als die geraden. Dies liegt daran, dass bei ungeradem Gewicht einer Hälfte die "überzählige" Eins sich zunächst an einer ungeraden Position der Sortierreihenfolge befindet. Nach Schritt 1 befindet sie sich somit in einer ungeraden Spalte.
In Schritt 2 werden durch die unshuffle-Operation alle geraden Spalten nach links, alle ungeraden Spalten nach rechts verschoben. Das Gewicht der rechten Hälfte ist anschließend um höchstens 2 größer als das der linken Hälfte.
In Schritt 3 werden die linke und die rechte Hälfte rekursiv sortiert.
Anschließend wird die Permutation der Schritte 1 und 2 wieder rückgängig gemacht (Schritte 4 und 5).
Das Ergebnis ist eine Folge, die aus zwei ineinander verschränkten (geshuffelten) sortierten Folgen besteht, von denen die zweite ein um höchstens 2 höheres Gewicht als die erste hat. In Schritt 6 wird die dadurch entstehende unsortierte Zone auf der Schlangenlinie mit 2 oets-Schritten bereinigt (tatsächlich genügt sogar ein Schritt, wenn mit dem richtigen Schritt (odd) angefangen wird).
2. Fall: m = 2
Die Korrektheit von 2-column-merge wird anhand von Bild 3 dargestellt.
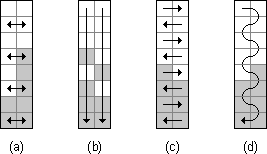
Bild 3: Verschmelzen zweier sortierter Spalten
Ausgangssituation ist ein k × 2-Feld, dessen beide Spalten sortiert sind (a). Durch die Vertauschung in ungeraden Zeilen werden die Einsen gleichmäßig auf beide Spalten verteilt (b). Dann werden die Spalten sortiert. Eine Spalte kann eine Eins mehr enthalten als die andere (c). Tatsächlich genügt ein Even-Schritt von Odd-even Transposition Sort, um das Feld in Schlangenlinie zu sortieren (d).
Analyse von 2-way-merge
Mit T(k, m) sei die Anzahl der Operationen von 2-way-merge(k, m) bezeichnet. T(k, 2) ist die Anzahl der Operationen von 2-column-merge(k). Für m > 2 ergibt sich folgende Anzahl von Operationen T(k, m) :
| Schritt 1 | 1 | |
| Schritt 2 | m/2 – 1 | |
| Schritt 3 | T(k, m/2) | |
| Schritt 4 | m/2 – 1 | |
| Schritt 5 | 1 | |
| Schritt 6 | 2 |
Die Schritte 1, 2 und 4, 5 benötigen zusammen genau m Operationen. Somit ist für m > 2
T(k, m) = m + 2 + T(k, m/2)
Mit T(k, 2) = k + 3 ergibt sich
T(k, m) = k + 2m + 2 log(m) – 3
Sortieren mit 2-way-merge
Aus dem Merge-Verfahren lässt sich rekursiv ein Sortierverfahren für ein n × n-Feld konstruieren. Da jedoch nur in horizontaler Richtung jeweils eine Reduktion der Feldgröße um die Hälfte stattfindet, liegt die Komplexität dieses Verfahrens in O(n·log(n)).
Es liegt daher nahe, die Feldgröße in jedem Rekursionsschritt des Sortierverfahrens auch in vertikaler Richtung zu halbieren. Entsprechend wird dann ein Merge-Verfahren benötigt, das nicht nur zwei, sondern vier sortierte Teilfelder verschmelzen kann. Das folgende Verfahren kann sogar 2s sortierte Teilfelder verschmelzen (s Zweierpotenz).
2s-way-merge
Prozedur 2s-way-merge(k, m, s)
Eingabe:
k × m-Feld (k > s, m > 1), bestehend aus 2s in Schlangenlinie sortierten Teilfeldern der Größe k/s × m/2 (Bild 1b)
Ausgabe:
das in Schlangenlinie sortierte k × m-Feld
Methode:
- wenn m > 2 dann
- oddexchange
- unshuffle in den Zeilen
- 2s-way-merge(k, m/2, s) rekursiv auf linke und rechte Hälfte anwenden
- shuffle in den Zeilen
- oddexchange
- 2s oets-Schritte auf der Schlangenlinie
- sonst
- 2s-column-merge(k, s)
Die Rekursion bricht ab, wenn jeweils nur noch zwei Spalten zu verschmelzen sind. Dann wird das folgende Verfahren 2s-column-merge verwendet.
Prozedur 2s-column-merge(k, s)
Eingabe:
k × 2-Feld, dessen linke und rechte Spalte jeweils aus sortierten Abschnitten der Länge k/s besteht
Ausgabe:
das in Schlangenlinie sortierte k × 2-Feld
Methode:
- oddexchange
- Sortieren der Spalten
- 2s oets-Schritte auf der Schlangenlinie
Das Verfahren 2-way-merge ergibt sich als Spezialfall von 2s-way-merge mit s = 1.
Korrektheit von 2s-way-merge
1. Fall: m > 2
Schritt 1 bezieht sich eigentlich auf die ungeraden Zeilen der Teilfelder. Diese sind jedoch identisch mit den ungeraden Zeilen des Gesamtfeldes, da k/s ein Vielfaches von 2 ist. Analog zu Schritt 1 von 2-way-merge kommen maximal 2s "überzählige" Einsen in die ungeraden Spalten.
Nach Schritt 2 ist somit das Gewicht der rechten Hälfte um höchstens 2s größer als das der linken Hälfte.
In Schritt 3 wird 2s-way-merge rekursiv aufgerufen. Die Rekursion endet, wenn m = 2 ist, d.h. wenn das zu sortierende Feld nur noch aus zwei Spalten besteht. Dieses wird dann durch 2s-column-merge sortiert.
Das Ergebnis nach Schritt 5 ist eine Folge, die aus zwei ineinander verschränkten (geshuffelten) sortierten Folgen besteht, von denen die zweite ein um höchstens 2s höheres Gewicht als die erste hat.
In Schritt 6 wird die dadurch entstehende unsortierte Zone auf der Schlangenlinie mit 2s oets-Schritten bereinigt.
2. Fall: m = 2
Durch die Vertauschung in ungeraden Zeilen werden die Einsen annähernd gleichmäßig auf beide Spalten verteilt. In jedem der s Abschnitte kann auf einer Seite eine Eins mehr sein als auf der anderen Seite. Dann werden die Spalten sortiert. Eine Spalte kann maximal s Einsen mehr enthalten als die andere. Dadurch ergibt sich eine unsortierte Zone der Länge höchstens 2s auf der Schlangenlinie, der durch 2s oets-Schritte sortiert wird.
Analyse von 2s-way-merge
Mit T(k, m, s) sei die Anzahl der Operationen von 2s-way-merge(k, m, s) bezeichnet. T(k, 2, s) ist die Anzahl der Operationen von 2s-column-merge(k, s).
| Schritt 1 | 1 | |
| Schritt 2 | m/2 – 1 | |
| Schritt 3 | T(k, m/2, s) | |
| Schritt 4 | m/2 – 1 | |
| Schritt 5 | 1 | |
| Schritt 6 | 2s |
Die Schritte 1, 2 und 4, 5 benötigen zusammen genau m Operationen. Somit gilt für m > 2
T(k, m, s) = m + 2s + T(k, m/2, s)
Mit T(k, 2, s) = k + 2s + 1 ergibt sich
T(k, m, s) = k + 2m + log(m)·2s – 3
Sortieren mit 2s-way-merge
Ein durch rekursive Anwendung von 2s-way-merge realisiertes Sortierverfahren für ein n × n-Feld hat somit z.B. mit s = 2 die Komplexität 2n + 4n + o(n) = 6n + o(n).
Eine Vereinfachung des entsprechenden Verfahrens ist in [LSSS 85] angegeben.
s2-way-merge
Ein noch effizienteres Sortierverfahren ergibt sich, wenn das n × n-Feld in s2 Blöcke unterteilt wird, die jeweils für sich sortiert und dann verschmolzen werden. Wird s = n1/3 gewählt, so erreicht das Sortierverfahren eine Komplexität von 3n + o(n).
Prozedur s2-way-merge(k, m, s)
Eingabe:
k × m-Feld (k > s, m ≥ s), bestehend aus s2 in Schlangenlinie sortierten Teilfeldern der Größe k/s × m/s (Bild 1c)
Ausgabe:
das in Schlangenlinie sortierte k × m-Feld
Methode:
- wenn m > s dann
- oddexchange
- unshuffle in den Zeilen
- s2-way-merge(k, m/2, s) rekursiv auf linke und rechte Hälfte anwenden
- shuffle in den Zeilen
- oddexchange
- s2 oets-Schritte auf der Schlangenlinie
- sonst
- s2-column-merge(k, s)
Die Rekursion bricht ab, wenn jeweils nur noch s Spalten zu verschmelzen sind. Dann wird das folgende Verfahren s2-column-merge verwendet.
Prozedur s2-column-merge(k, s)
Eingabe:
k × s-Feld (k > s), bestehend aus s2 sortierten Teilfeldern der Größe k/s × 1
Ausgabe:
das in Schlangenlinie sortierte k × s-Feld
Methode:
- für r = 1 bis log(s)-1 wiederhole
- 2-way-merge(k/s, 2r) auf alle Teilfelder der Größe k/s × 2r anwenden
- 2s-way-merge(k, s, s)
Korrektheit von s2-way-merge
Der Beweis der Korrektheit von s2-way-merge lässt sich analog zum Beweis von 2s-way-merge führen.
Analyse von s2-column-merge
Die Analyse von s2-column-merge ergibt zunächst recht komplizierte Ausdrücke für die Anzahl der Operationen. Mit k = n und s = n1/3 lassen sich diese jedoch wie angegeben abschätzen.
| Schritt 1 | (log(s)-1) · (k/s + log(s) – 3) + 2s – 4 | ∈ O(n2/3·log(n)) | ||
| Schritt 2 | k + 2s + log(s)·2s – 3 | ∈ n + O(n1/3·log(n)) |
Analyse von s2-way-merge
Mit T(k, m, s) sei die Anzahl der Operationen von s2-way-merge(k, m, s) bezeichnet. T(k, s, s) ist die Anzahl der Operationen von s2-column-merge(k, s).
| Schritt 1 | 1 | |
| Schritt 2 | m/2 – 1 | |
| Schritt 3 | T(k, m/2, s) | |
| Schritt 4 | m/2 – 1 | |
| Schritt 5 | 1 | |
| Schritt 6 | s2 |
Die Schritte 1, 2 und 4, 5 benötigen zusammen genau m Operationen. Somit gilt für m > s
T(k, m, s) = m + s2 + T(k, m/2, s)
Daraus ergibt sich
T(k, m, s) ≤ 2m + log(m)·s2 + T(k, s, s)
Mit k = m = n und s = n1/3 lässt sich die Komplexität von s2-way-merge abschätzen als
T ∈ 3n + O(n2/3·log(n))
Sortieren mit s2-way-merge
Ein mit s2-way-merge realisiertes Sortierverfahren für ein n × n-Feld hat somit ebenfalls eine Komplexität von 3n + O(n2/3·log(n)), da sich die Blöcke der Seitenlänge n2/3 in Zeit O(n2/3) sortieren lassen (z.B. mit dem auf 2s-way-merge aufgebauten Sortierverfahren).
Simulation
Die folgende Simulation zeigt den Ablauf des Algorithmus von Thompson-Kung mit einem 64 × 64-Feld von Nullen und Einsen. Zur besseren Anschaulichkeit werden einige Operationen sequentiell angezeigt, auch wenn sie auf einem zweidimensionalen Prozessorfeld parallel ablaufen könnten.
(Java-Applet zur Simulation des Algorithmus von Thompson-Kung)
Literatur
[Bat 68] K.E. Batcher: Sorting Networks and their Applications. Proc. AFIPS Spring Joint Comput. Conf., Vol. 32, 307-314 (1968)
[LSSS 85] H.W. Lang, M. Schimmler, H. Schmeck, H. Schröder: Systolic Sorting on a Mesh-Connected Network. IEEE Transactions on Computers C-34, 7, 652-658 (1985)
[TK 77] C.D. Thompson, H.T. Kung: Sorting on a Mesh-Connected Parallel Computer. Communications of the ACM, 20, 4, 263-271 (1977)
Weiter mit: [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 15.06.2001 Updated: 07.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden