Mathematische Grundlagen
Menge, Relation, Abbildung
Menge
Das grundlegendste Konzept in der Mathematik ist die Mengenlehre.
Mengenbildung
Definition: Eine Menge ist eine Zusammenfassung von wohlbestimmten und wohlunterschiedenen Objekten zu einem Ganzen (G. Cantor
, 1895).
Die Objekte einer Menge A heißen Elemente von A.
Durch Mengenbildung wird aus mehreren Objekten ein neues Objekt gemacht, die Menge.
Schreibweise:
| a ist Element der Menge A: | a ∈ A | (Elementzeichen) | ||
| A besteht aus den Elementen a, b und c: | A = {a, b, c} | (Mengenklammern) |
Beispiel: Beispiele für Mengen sind:
{4, 5, 7}
{1, 2, 3, 4, ... } (eine Menge mit unendlich vielen Elementen)
{ {a}, {a, b} } (eine Menge, deren Elemente wiederum Mengen sind)
{ } = ∅ (leere Menge)
{ ∅ } (eine Menge, deren einziges Element die leere Menge ist)
Für die grundlegenden Mengen von Zahlen werden folgende Bezeichnungen verwendet:
ℕ = { 1, 2, 3, ... } (natürliche Zahlen)
ℕ0 = { 0, 1, 2, 3, ... } (natürliche Zahlen einschließlich der Null)
ℤ = { ..., -3, -2, -1, 0, 1, 2, 3, ... } (ganze Zahlen)
ℚ (rationale Zahlen)
ℝ (reelle Zahlen)
ℂ (komplexe Zahlen)
Es ist auch möglich, Objekte mit einer gemeinsamen Eigenschaft E(x) zu einer Menge zusammenzufassen.
Schreibweise: { x | E(x) } (die Menge aller x, für die E(x) gilt)
Beispiel: { n | ∃ k ∈ ℕ : k2 = n } = {1, 4, 9, 16, 25, ...} (Quadratzahlen)
{ x | x ∈ ℕ ∧ x < 5 } = {1, 2, 3, 4} (alle natürlichen Zahlen, die kleiner als 5 sind)
{ x | x ≠ x } = ∅ (leere Menge)
Gehört zu der gemeinsamen Eigenschaft E(x), dass x aus einer schon vorhandenen Grundmenge stammt oder dass x durch Anwendung einer Operation zustande kommt, so lässt sich die Schreibweise abkürzen (vergl. gegenüber vorigem Beispiel)
Beispiel: { x ∈ ℕ | x < 5 } = {1, 2, 3, 4}
{ k2 | k ∈ ℕ } = {1, 4, 9, 16, 25, ...}
Operationen auf Mengen
Definition: Seien A und B Mengen.
Die Vereinigung von A und B ist die Menge
A ∪ B = { x | x ∈ A ∨ x ∈ B }.
Der Durchschnitt von A und B ist die Menge
A ∩ B = { x | x ∈ A ∧ x ∈ B }.
Die Differenz von A und B ist die Menge
A \ B = { x | x ∈ A ∧ x ∉ B }.
Beispiel: {1, 3, 5} ∪ {1, 2, 3} = {1, 2, 3, 5}
{1, 3, 5} ∩ {1, 2, 3} = {1, 3}
{1, 3, 5} \ {1, 2, 3} = {5}
Definition: Zwei Mengen A und B heißen disjunkt, wenn A ∩ B = ∅ gilt, d.h. wenn ihr Durchschnitt die leere Menge ist.
Satz: (Rechenregeln)
Für alle Mengen A, B, C gilt:
| (A ∪ B) ∪ C = A ∪ (B ∪ C) | (Assoziativität) | |
| (A ∩ B) ∩ C = A ∩ (B ∩ C)_ | ||
| A ∪ B = B ∪ A | (Kommutativität) | |
| A ∩ B = B ∩ A_ | ||
| A ∪ A = A | (Idempotenz) | |
| A ∩ A = A_ | ||
| A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C) | (Distributivität) | |
| A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C) |
Teilmenge
Definition: Seien A und B Mengen. A ist enthalten in B oder A ist Teilmenge von B, wenn alle Elemente von A auch Elemente von B sind:
A ⊆ B ⇔ ∀ x : (x ∈ A ⇒ x ∈ B).
Beispiel: {1, 5} ⊆ {1, 3, 5}
{2, 4, 6, 8, ... } ⊆ ℕ
{1, 2, 3} ⊆ {1, 2, 3}
Satz: Es gelten folgende Beziehungen für alle Mengen A, B, C :
A ⊆ A,
A ⊆ B ∧ B ⊆ A ⇔ A = B,
A ⊆ B ∧ B ⊆ C ⇒ A ⊆ C
sowie
∅ ⊆ A.
Komplement
Oft ist eine bestimmte Grundmenge G fest vorgegeben, z.B. G = ℕ, und wir betrachten eine Teilmenge A ⊆ G. Dann wird die Differenz G \ A, also die Menge aller Elemente von G, die nicht zu A gehören, als das Komplement von A bezeichnet.
Definition: Sei G eine vorgegebene Menge und sei A ⊆ G. Dann ist
A = G \ A = { x ∈ G | x ∉ A }
das Komplement der Menge A.
Satz: (Rechenregeln)
Für die Grundmenge G sowie für alle Mengen A, B ⊆ G gilt:
G = ∅
A = A
A ∪ A = G
A ∪ ∅ = A
A ∪ G = G
Die letztgenannte Rechenregel wird als Regel vonDe Morgan bezeichnet.
Indem in den obenstehenden Regeln G und ∅ sowie ∪ und ∩ vertauscht werden, ergeben sich weitere, entsprechende duale Regeln.
Potenzmenge
Definition: Die Potenzmenge einer Menge A ist die Menge aller Teilmengen von A:
℘(A) = { M | M ⊆ A}.
Beispiel: ℘({1, 2, 3}) = { ∅ , {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3} }
℘( ∅ ) = { ∅ }
Die Potenzmenge einer endlichen Menge mit n Elementen hat 2n Elemente. So hat z.B. die Potenzmenge der obigen 3-elementigen Menge 23 = 8 Elemente. Die Potenzmenge der leeren Menge (0 Elemente) hat 20 = 1 Element.
Kartesisches Produkt
Definition: Das kartesische Produkt zweier Mengen A und B ist die Menge aller geordneten Paare von Elementen aus A bzw. B:
A × B = { (a, b) | a ∈ A, b ∈ B }.
Durch Paarbildung wird aus zwei Objekten ein neues Objekt gemacht, das Paar. Anders als bei der Mengenbildung kommt es hier jedoch auf die Reihenfolge der Komponenten an; die Komponenten brauchen auch nicht verschieden zu sein.
Die Paarbildung kann auf die Mengenbildung zurückgeführt werden, indem das geordnete Paar (a, b) als abkürzende Schreibweise für die Menge { {a}, {a, b} } angesehen wird (nach K. Kuratowski).
Zwei Paare (a, b) und (c, d) sind gleich, wenn a = c und b = d ist.
Definition: Das kartesische Produkt dreier Mengen A, B und C ist die Menge aller geordneten Tripel von Elementen aus A, B bzw. C:
A × B × C = { (a, b, c) | a ∈ A, b ∈ B, c ∈ C}.
Das n-fache kartesische Produkt einer Menge A ist die Menge aller n-Tupel von Elementen aus A:
An = A × . . . × A = { (a0, ..., an-1) | ai ∈ A, i = 0, ..., n-1}.
Es ist
A1 = A .
Relation
Eine Relation ist nichts anderes als eine Teilmenge eines kartesischen Produkts.
Definition: Seien A und B Mengen. Eine Teilmenge R ⊆ A × B heißt (zweistellige) Relation zwischen A und B. Gilt A = B, so heißt R Relation auf A.
Schreibweise: Statt (a, b) ∈ R schreibt man im Allgemeinen a R b; statt des Buchstabens R verwendet man bei Relationen meist spezielle Symbole: = , ≤ , < , ⊆ , ~ , ...
Beispiel: Die folgende Mengen stellen die Kleiner- bzw. die Gleichheitsrelation auf der Menge ℕ dar:
< = { (1,2), (1,3), (2,3), (1,4) ... } ⊆ ℕ × ℕ
= = { (1,1), (2,2), (3,3), (4,4) ... } ⊆ ℕ × ℕ
Eigenschaften von Relationen
Definition: Sei R eine Relation auf einer Menge A. R heißt
| reflexiv | ⇔ ∀ a ∈ A : | (a, a) ∈ R | ||
| antisymmetrisch | ⇔ ∀ a, b ∈ A : | (a,b) ∈ R ∧ (b, a) ∈ R ⇒ a = b | ||
| transitiv | ⇔ ∀ a, b, c ∈ A : | (a, b) ∈ R ∧ (b, c) ∈ R ⇒ (a, c) ∈ R | ||
| symmetrisch | ⇔ ∀ a, b ∈ A : | (a, b) ∈ R ⇔ (b, a) ∈ R | ||
| irreflexiv | ⇔ ∀ a ∈ A : | (a, a) ∉ R | ||
| total | ⇔ ∀ a, b ∈ A : | a ≠ b ⇒ (a, b) ∈ R ∨ (b, a) ∈ R |
Beispiel: Sei M die Menge aller Menschen. Die Relation 
("ist verheiratet mit") auf M ist symmetrisch (wenn a mit b verheiratet ist, dann ist auch b mit a verheiratet), irreflexiv (niemand ist mit sich selbst verheiratet), aber nicht total (es gibt unverheiratete Menschen).
Die Relation ~ ("hat dieselben Eltern wie") auf M ist reflexiv (jeder hat dieselben Eltern wie er selbst), symmetrisch (wenn a dieselben Eltern hat wie b, dann hat auch b dieselben Eltern wie a) und transitiv (wenn a dieselben Eltern hat wie b und b dieselben Eltern hat wie c, dann hat auch a dieselben Eltern wie c).
Die Relation 
("ist Vorfahre von") auf M ist antisymmetrisch (wenn a Vorfahre von b ist und b Vorfahre von a ist, dann sind a und b gleich – die Aussage ist wahr, da die ersten beiden Bedingungen nie gleichzeitig eintreten können), transitiv (wenn a Vorfahre von b ist und b Vorfahre von c ist, dann ist a Vorfahre von c) und irreflexiv (niemand ist Vorfahre von sich selbst).
Eine (nichtleere) Relation kann nicht gleichzeitig reflexiv und irreflexiv sein. Aber es gibt Relationen, die weder reflexiv noch irreflexiv sind. Ebenso gibt es Relationen, die weder symmetrisch noch antisymmetrisch sind, und Relationen, die gleichzeitig symmetrisch und antisymmetrisch sind (siehe Beispiele unten). Insofern verhalten sich die Begriffe nicht komplementär zueinander. Wir können nicht folgern: Die Relation ist nicht symmetrisch, also ist sie antisymmetrisch.
Beispiel: Sei A = {1, 2, 3}. Die folgenden Mengen R1, R2 und R3 sind Relationen auf A, und es gilt
R1 = { (1, 1), (1, 2) } ist nicht reflexiv und nicht irreflexiv,
R2 = { (1, 2), (2, 1), (1, 3) } ist nicht symmetrisch und nicht antisymmetrisch,
R3 = { (2, 2), (3, 3) } ist symmetrisch und antisymmetrisch.
Definition: Eine Relation heißt Halbordnung, wenn sie reflexiv, antisymmetrisch und transitiv ist.
Eine Relation heißt strenge Halbordnung, wenn sie irreflexiv und transitiv ist.1)
Eine Relation heißt lineare Ordnung oder totale Ordnung oder Ordnung, wenn sie Halbordnung ist und zusätzlich noch total ist.
Eine Relation heißt Äquivalenzrelation, wenn sie reflexiv, symmetrisch und transitiv ist.
Beispiel: Die Relationen ≤ und | ("teilt") auf ℕ sind Halbordnungen, ≤ ist sogar totale Ordnung.
Die Relation ≡ n ("ist kongruent modulo n", d.h. liefert bei ganzzahliger Division durch n denselben Rest) ist eine Äquivalenzrelation auf ℤ.
Die Relation auf der Menge der Menschen M ist eine strenge Halbordnung. Die Relation ~ auf M ist eine Äquivalenzrelation.
Äquivalenzrelationen auf einer Menge A bewirken eine Klasseneinteilung von A, d.h. eine Zerlegung von A in paarweise disjunkte Mengen (Äquivalenzklassen).
Die Äquivalenzrelation ≡ 2 bewirkt eine Klasseneinteilung von ℤ in die geraden und die ungeraden Zahlen. Die Äquivalenzklassen der Relation ~ auf der Menge der Menschen sind die Geschwister.
Operationen auf Relationen
Definition: Das Produkt zweier Relationen R, T ⊆ A × A ist die Relation
RT = { (a, c) | ∃ b ∈ A : (a, b) ∈ R ∧ (b, c) ∈ T }.
Potenzen einer Relation R ⊆ A × A sind wie folgt definiert:
R0 = { (a, a) | a ∈ A },
Ri = Ri-1 R für alle i ∈ ℕ.
Definition: Die transitive Hülle einer Relation R ist die Relation
R+ = 
i ∈ IN Ri = R ∪ R2 ∪ R3 ∪ . . .
Die reflexive Hülle einer Relation R ist die Relation
R? = R0 ∪ R.
Die reflexive und transitive Hülle einer Relation R ist die Relation
R* = i ∈ IN0 Ri = R0 ∪ R+ .
Die Hülle einer Relation R bezüglich einer Eigenschaft ergibt sich, indem die fehlenden Elemente hinzugenommen werden. D.h. die Hülle ist die kleinste Relation, die R umfasst und die betreffende Eigenschaft hat.
Aus einer strengen Halbordnung R lässt sich eine Halbordnung H machen, indem die reflexive Hülle H = R0 ∪ R gebildet wird. Umgekehrt ergibt sich die zu einer Halbordnung H gehörige strenge Halbordnung R, indem R = H \ H0 gebildet wird.
Definition: Die inverse Relation von R ⊆ A × A ist die Relation
R -1 = { (b, a) | (a, b) ∈ R }.
Beispiel: Sei M die Menge der Menschen und 
die Relation "ist Elternteil von" auf M. Die Relation -1 bedeutet dann "ist Kind von", die Relation 2 bedeutet "ist Großelternteil von" und die Relation + ist identisch mit der Relation ("ist Elternteil oder Großelternteil oder Urgroßelternteil oder ..., d.h. ist Vorfahre von").
Das Produkt der Relationen ("ist Elternteil von") und ("ist verheiratet mit") ist die Relation . Zwei Menschen a und c stehen in der Relation , wenn es einen Menschen b gibt, sodass a Elternteil von b ist und b mit c verheiratet ist. Damit ist a Schwiegermutter oder Schwiegervater von c.
Abbildung
Abbildungen sind spezielle zweistellige Relationen. Während eine Relation eine völlig beliebige Teilmenge eines kartesischen Produktes ist, werden an eine Abbildung zwei bestimmte Bedingungen gestellt. Dies kommt in der folgenden Definition zum Ausdruck.
Definition: Seien A und B Mengen. Eine Abbildung ist eine Relation f ⊆ A × B mit den folgenden Eigenschaften (1) und (2). Wegen der Gültigkeit dieser Eigenschaften ist bei Abbildungen folgende Schreibweise üblich:
| f : A → B | statt | f ⊆ A × B | und | |||
| f(a) = b | statt | (a, b) ∈ f. |
| (1) | eindeutig | ∀ a, a' ∈ A : a = a' ⇒ f(a) = f(a') |
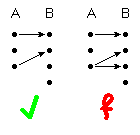
(von jedem Punkt geht höchstens ein Pfeil aus)
| (2) | total definiert | ∀ a ∈ A ∃ b ∈ B : f(a) = b |
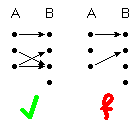
(von jedem Punkt geht mindestens ein Pfeil aus)
(1) und (2) zusammen ergeben: von jedem Punkt geht genau ein Pfeil aus (die Abbildung ist wohldefiniert). Eine Relation, die nur (1) erfüllt, wird als partielle Abbildung bezeichnet.
| (1) + (2) | Abbildung |
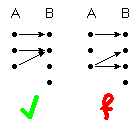
(von jedem Punkt geht genau ein Pfeil aus)
Genau wie eine Relation ist also eine Abbildung nichts anderes als eine Menge von Paaren, die allerdings die genannten Bedingungen (1) und (2) erfüllen muss. Ein anderes Wort für Abbildung ist Funktion. Gelegentlich trifft man auf Formulierungen wie "die Funktion y = 3x2 ". Gemeint ist hierbei "die Funktion mit der Funktionsgleichung y = 3x2 ", und dies ist die Menge { (x, y) | y = 3x2}, also die Menge aller Paare (x, y), die der Funktionsgleichung genügen.
Definition: Sei f : A → B eine Abbildung, d.h. f erfüllt (1) und (2). Die Abbildung f heißt injektiv, wenn f die folgende Eigenschaft (3) hat; f heißt surjektiv, wenn f die folgende Eigenschaft (4) hat; f heißt bijektiv, wenn f beide Bedingungen (3) und (4) erfüllt.
| (3) | injektiv | ∀ a, a' ∈ A : a ≠ a' ⇒ f(a) ≠ f(a') |
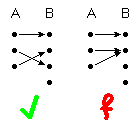
(bei jedem Punkt kommt höchstens ein Pfeil an)
| (4) | surjektiv | ∀ b ∈ B ∃ a ∈ A : f(a) = b |
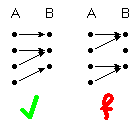
(bei jedem Punkt kommt mindestens ein Pfeil an)
(3) und (4) zusammen ergeben: bei jedem Punkt kommt genau ein Pfeil an (die Abbildung ist bijektiv). Dies bedeutet, dass die inverse Relation f -1 der Abbildung f auch eine Abbildung ist (sogar ebenfalls eine bijektive Abbildung).
| (3) + (4) | bijektiv |
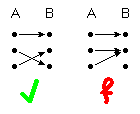
(bei jedem Punkt kommt genau ein Pfeil an)
Tatsächlich wissen schon kleine Kinder, was eine bijektive Abbildung ist. Beim Zählen nämlich kommt es darauf an, eine bijektive Abbildung herzustellen zwischen der Menge der Gegenstände, die gezählt werden sollen, und der Menge {1, ..., n} (vergl. nächster Abschnitt: Mächtigkeit einer Menge). Sollen beispielsweise Stofftiere gezählt werden, so stellt das Kind die Abbildung her, indem es unter Beachtung der Bedingungen (1) bis (4) jeweils auf ein Stofftier zeigt und dabei eine Zahl sagt.
Ganz kleine Kinder, die noch nicht richtig zählen können, verletzen regelmäßig mindestens eine der Bedingungen (1) bis (4). So zeigt das Kind etwa mehrfach auf ein Stofftier oder vergisst eines. Oder es zeigt zwar auf alle Stofftiere, sagt dabei aber die Zahlen "1, 2, 3, 2, 4". Oder es sagt die Zahlen "1, 2, 5, 6, 8".
Mächtigkeit, Folge, Permutation
Definition: Die Mächtigkeit |A| einer Menge A ist wie folgt definiert:
| |A| = |  |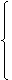
|
Eine Menge mit der Mächtigkeit n ∈ ℕ0 heißt endliche Menge. Bei endlichen Mengen ist die Mächtigkeit gleich der Anzahl der Elemente. Eine Menge, die nicht endlich ist, heißt unendliche Menge.
Bei unendlichen Mengen kann man den Begriff der Mächtigkeit nicht mehr anschaulich mit der Anzahl der Elemente verbinden. So sind etwa die Mengen ℕ und ℤ gleich mächtig, obwohl ℕ anschaulich "weniger" Elemente enthält als ℤ. Andererseits sind auch wieder nicht alle unendlichen Mengen gleich mächtig.
Definition: Zwei Mengen A und B sind gleich mächtig, wenn es eine bijektive Abbildung zwischen ihnen gibt:
|A| = |B| ⇔ ∃ bijektive Abbildung f : A ⟷ B
Offenbar gibt es eine bijektive Abbildung zwischen ℕ und ℤ, etwa gemäß folgender Wertetabelle:
Andererseits gibt es keine bijektive Abbildung zwischen den unendlichen Mengen ℕ und ℝ, daher sind diese beiden Mengen nicht gleich mächtig. Es gibt also offenbar verschiedene Grade des Unendlichen.
Die Mächtigkeit ℵ0 wird als abzählbar unendlich bezeichnet. Eine Menge ist abzählbar unendlich, wenn sie gleich mächtig zu den natürlichen Zahlen ist. Die Bezeichnung ℵ0 geht auf Cantor zurück. Das Zeichen ℵ (aleph) ist der erste Buchstabe des hebräischen Alphabets. Die Mächtigkeit ℵ0 ist die kleinste Mächtigkeit, die eine unendliche Menge haben kann.
Eine Menge, die entweder endlich oder abzählbar unendlich ist, wird als abzählbar bezeichnet. Offenbar ist eine Menge M abzählbar, wenn es eine surjektive Abbildung von ℕ auf M gibt.
Eine unendliche Menge, die nicht abzählbar unendlich ist, wird als überabzählbar unendlich bezeichnet. So ist beispielsweise ℝ überabzählbar unendlich. Das Zeichen 𝔠 bedeutet "Mächtigkeit des Kontinuums".
Beispiel: Einige Beispiele für die Mächtigkeit von Mengen:
| {1, 2, 5, 7} | = 4
| {2, 4, 6, 8, ... } | = ℵ0
|ℤ| = ℵ0
|ℚ| = ℵ0
| [0,1] | = 𝔠
|ℂ| = 𝔠
|ℝn| = 𝔠
|℘(ℕ)| = 𝔠
Definition: Sei A eine Menge. Unter einer Folge versteht man eine Abbildung
a : ℕ0 → A.
Eine endliche Folge ist eine Abbildung
a : {0, ..., n-1} → A, n ∈ ℕ0.
Hierbei ist n die Länge der endlichen Folge.
Wir schreiben endliche Folgen so: a = a0, ..., an-1. Endliche Folgen lassen sich auch als n-Tupel (a0, ..., an-1) auffassen, d.h. als Elemente des kartesischen Produktes An.
Definition: Eine Permutation ist eine bijektive Abbildung
p : {0, ..., n-1} → {0, ..., n-1}, n ∈ ℕ.
Beispiel: Die endliche Folge p = 4, 1, 2, 0, 3 ist eine Permutation.
Literatur
1) Der Begriff "strenge Halbordnung" ist etwas unglücklich, da er wie "Halbordnung, und zusätzlich noch streng" klingt. Tatsächlich ist aber eine strenge Halbordnung nicht reflexiv und daher keine Halbordnung im Sinne der obigen Definition, sondern eine "andere Art von Halbordnung".
Weiter mit: [Graph] [Literatur] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 15.09.1997 Updated: 10.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden