Sortieren auf zweidimensionalen Prozessorfeldern
3n-Sort
Das Verfahren 3n-Sort von Schnorr und Shamir [SchSh 86] ist komplizierter als etwa Rotatesort oder LS3-Sort. Mit einer Zeitkomplexität von 3n + O(n3/4) ist es jedoch optimal, denn 3n ist eine untere Schranke für das Sortieren auf einem zweidimensionalen Prozessorfeld.
Verfahren
Das n×n-Feld wird in senkrechte Scheiben, waagerechte Scheiben und Blöcke unterteilt. Eine senkrechte Scheibe ist ein n×n3/4-Teilfeld, eine waagerechte Scheibe ist ein n3/4×n-Teilfeld und ein Block ist ein n3/4×n3/4-Teilfeld (Bild 1).
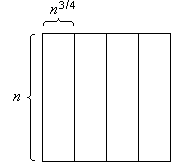
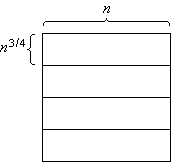
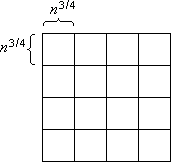
Bild 1: Senkrechte Scheiben (a), waagerechte Scheiben (b) und Blöcke (c)
Das gesamte Feld wie auch Teilfelder (Blöcke, Scheiben) werden stets in Schlangenlinie sortiert.
Der Algorithmus von Schnorr-Shamir verwendet folgende Operation unshuffle sowie die Operation oets (Schritt von Odd-even Transposition Sort.
unshuffle
Eine k-fach-unshuffle-Operation ist eine Permutation, die dem Austeilen von n Karten an k Spieler entspricht (k ist Teiler von n).
Beispiel: Permutation 4-fach-unshuffle der Zahlen 0, ..., 11
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 0 | 4 | 8 | 1 | 5 | 9 | 2 | 6 | 10 | 3 | 7 | 11 |
Spieler 1 erhält die Karten 0, 4 und 8, Spieler 2 die Karten 1, 5 und 9 usw.
Im Algorithmus 3n-Sort wird ein n1/4-fach-unshuffle der Elemente der Zeilen durchgeführt.
Algorithmus 3n-Sort
Eingabe:
Unsortiertes n×n-Feld von Daten
Ausgabe:
Das sortierte n×n-Feld
Methode:
- sortiere die Blöcke
- wende n1/4-fach-unshuffle entlang der Zeilen an
- sortiere die Blöcke
- sortiere die Spalten
- sortiere die senkrechten Scheiben
- sortiere die Zeilen in gegenläufige Richtung
- wende n3/4 oets-Schritte auf der Schlangenlinie an
Gegenläufiges Sortieren bedeutet, dass jede Zeile i aufsteigend sortiert wird, wenn i gerade ist, und absteigend, wenn i ungerade ist (i ∈ {0, ..., n-1}).
Korrektheit
Die Korrektheit von 3n-Sort wird wiederum mit Hilfe des 0-1-Prinzips gezeigt. In den folgenden Abbildungen sind Nullen weiß und Einsen grau dargestellt.
Definition: Eine Zeile heißt einfarbig, wenn sie nur aus Nullen oder nur aus Einsen besteht, anderenfalls heißt sie gemischt. Eine gemischte Zeile in einem sortierten Feld heißt angefangene Zeile.
Definition: Das Gewicht eines r × s-Teilfeldes ist gleich der Anzahl der Einsen in diesem Teilfeld.
Insbesondere bezieht sich diese Definition hier auf Spalten und auf Blöcke.
Definition: Ein maximaler zusammenhängender Bereich in der Sortierreihenfolge, der mit einer Eins beginnt und mit einer Null endet, heißt unsortierte Zone.
Eine 0-1-Folge mit einer unsortierten Zone beginnt mit Nullen, dann kommt ein Gemisch von Einsen und Nullen, und dann kommen Einsen.
Schritt 1
Nach dem Sortieren der Blöcke enthält jeder Block höchstens eine angefangene Zeile (Bild 2a).
Schritt 2
Die Operation n1/4-fach-unshuffle verteilt jeweils die Spalten eines Blocks reihum auf alle n1/4 Blöcke derselben horizontalen Scheibe. Wenn der Block eine angefangene Zeile enthält, erhalten einige Blöcke jeweils eine Eins mehr als andere. Insgesamt kann dadurch ein Block höchstens n1/4 Einsen mehr als ein anderer erhalten, d.h. die Gewichte von je zwei Blöcken in der horizontalen Scheibe unterscheiden sich höchstens um n1/4 (Bild 2b).
Schritt 3
Nach dem erneuten Sortieren der Blöcke enthält jeder Block höchstens eine angefangene Zeile (Bild 2c).
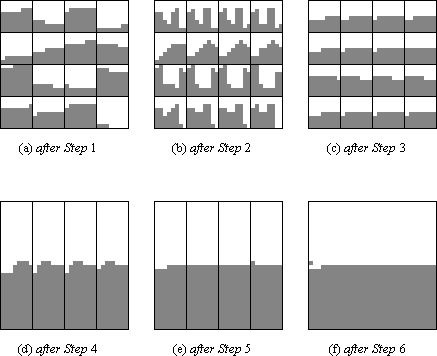
Bild 2: Situationen während der Ausführung des Algorithmus
Schritt 4
Nach dem Sortieren der Spalten enthält jede senkrechte Scheibe höchstens n1/4 gemischte Zeilen (die angefangenen Zeilen ihrer n1/4 Blöcke).
Ferner unterscheiden sich die Gewichte von je zwei senkrechten Scheiben um höchstens n1/4 · n1/4 = n1/2 (Bild 2d).
Schritt 5
Nach dem Sortieren der senkrechten Scheiben haben alle senkrechten Scheiben fast gleich viele 1-Zeilen: der Unterschied beträgt höchstens 1. Dies liegt daran, dass aufgrund der Breite der senkrechten Scheibe von n3/4 ein Gewichtsunterschied von n1/2 höchstens eine zusätzliche volle 1-Zeile erzeugen kann.
Wir nennen den Bereich der Länge n1/2 auf der Schlangenlinie, innerhalb dessen eine senkrechte Scheibe zusätzliche Einsen gegenüber einer anderen senkrechten Scheibe enthalten kann, den kritischen Bereich (umrahmt dargestellt in Bild 3a).
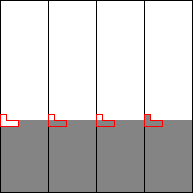
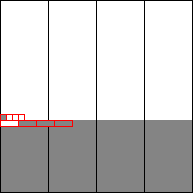
Bild 3: Kritische Bereiche in den senkrechten Scheiben: (a) vor Schritt 6 und (b) nach Schritt 6
Das gesamte Feld enthält insgesamt nur noch höchstens 2 gemischte Zeilen (Bild 2e).
Schritt 6
In Schritt 6 werden die beiden verbliebenen gemischten Zeilen gegenläufig sortiert. Möglicherweise noch nicht fertig sortiert sind jetzt nur noch die höchstens n1/4 · n1/2 = n3/4 Elemente aus den kritischen Bereichen (Bild 3b / Bild 2f). Es verbleibt also eine unsortierte Zone der Länge höchstens n3/4 auf der Schlangenlinie.
Schritt 7
In Schritt 7 wird die unsortierte Zone der Länge höchstens n3/4 entlang der Schlangenlinie fertig sortiert.
Dem 0-1-Prinzip zufolge sortiert das Verfahren jeden beliebigen Datensatz, da es nach obiger Argumentation alle 0-1-Datensätze sortiert.
Analyse
Die Analyse des Algorithmus ergibt folgendes:
| Schritt 1: | Sortieren der Blöcke | O(n3/4) | ||
| Schritt 2: | unshuffle entlang der Zeilen | n | ||
| Schritt 3: | Sortieren der Blöcke | O(n3/4) | ||
| Schritt 4: | Sortieren der Spalten | n | ||
| Schritt 5: | Sortieren der senkrechten Scheiben | O(n3/4) | ||
| Schritt 6: | Zeilen gegenläufig sortieren | n | ||
| Schritt 7: | n3/4 oets-Schritte | O(n3/4) | ||
| insgesamt: | 3n + O(n3/4) |
Das Sortieren der Blöcke kann mit irgendeinem linearen Sortierverfahren durchgeführt werden, z.B. mit LS3-Sort.
Die senkrechten Scheiben lassen sich in Schritt 5 in O(n3/4) sortieren, weil sie nur einen Bereich von n1/4 gemischten Zeilen enthalten (z.B. durch Sortieren der Blöcke und anschließendes Sortieren der um n1/4 Zeilen nach unten versetzten Blöcke).
Zusammenfassung
Der vorgestellte Algorithmus 3n-Sort von Schnorr-Shamir zum Sortieren eines n×n-Feldes hat eine Zeitkomplexität von 3n + O(n3/4). Es ist daher sowohl asymptotisch optimal als auch hinsichtlich der Konstanten, denn 3n ist eine untere Schranke für das Sortieren auf einem n×n-Feld. Der Algorithmus von Schnorr-Shamir ist einfacher als der Algorithmus von Thompson-Kung [TK 77], der mit einer Zeitkomplexität von 3n + O(n2/3·log(n)) ebenfalls optimal ist.
Literatur
[SchSh 86] C.P. Schnorr, A. Shamir: An Optimal Sorting Algorithm for Mesh-Connected Computers. Proc. of the 18th ACM Symposium on Theory of Computing, 255-261 (1986)
[TK 77] C.D. Thompson, H.T. Kung: Sorting on a Mesh-Connected Parallel Computer. Communications of the ACM, 20, 4, 263-271 (1977)
[Lan 12] H.W. Lang: Algorithmen in Java. 3. Auflage, Oldenbourg (2012)
Das Verfahren 3n-Sort finden Sie auch in meinem Buch über Algorithmen.
Weitere Themen des Buches: Sortieren, Textsuche, Parsen und Übersetzen, Graphenalgorithmen, Arithmetik, Codierung, Kryptografie.
Themen des Buches: Sortieren, Textsuche, Parsen und Übersetzen, Graphenalgorithmen, Arithmetik, Codierung, Kryptografie.
Weiter mit: [Sortierverfahren von Thompson-Kung] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 23.05.2001 Updated: 07.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden
