Sortiernetze
Odd-even Transposition Sort
Verfahren
Das Sortiernetz Odd-even Transposition Sort [Knu 73] für n Eingabedaten besteht aus n Vergleicherstufen, in denen jeweils abwechselnd alle Eingabedaten mit ungeradem Index mit ihren darüber liegenden Nachbarn verglichen werden und dann alle Eingabedaten mit geradem Index (Bild 1). Die Anzahl der Vergleicher beträgt n·(n-1)/2 und entspricht damit genau derjenigen von Bubblesort, die Anzahl der Vergleicherstufen ist jedoch nur etwa halb so groß.

Bild 1: Sortiernetz Odd-even Transposition Sort für n = 8
Korrektheit
Es wird gezeigt, dass Odd-even Transposition Sort jede beliebige Folge von Nullen und Einsen sortiert. Nach dem 0-1-Prinzip wird dann auch jede Folge von beliebigen Elementen sortiert. Der Beweis wird durch vollständige Induktion über die Problemgröße n geführt.
Behauptung: Das Odd-even-Transposition-Vergleichernetz für n Elemente sortiert jede 0-1-Folge der Länge n.
Induktionsanfang: n = 1
Das Odd-even-Transposition-Vergleichernetz für ein Element besteht aus lediglich einer durchgezogenen waagerechten Linie mit 0 Vergleichern. Da jede 0-1-Folge der Länge 1 bereits sortiert ist, ist die Behauptung für n = 1 bewiesen.
Induktionsannahme: Die Behauptung sei für n-1 erfüllt.
Induktionsschluss:
Gegeben sei ein Odd-even-Transposition-Vergleichernetz für n > 1 Elemente, ferner eine beliebige 0-1-Folge a = a0, ..., an-1.
1. Fall: Ist an-1 = 1, so bewirken die unteren Vergleicher [n-2:n-1] nichts und können entfallen. Es verbleibt ein Odd-even-Transposition-Vergleichernetz für n-1 Elemente (plus eine überflüssige Vergleicherstufe), das nach Induktionsannahme die Folge a0, ..., an-2 sortiert. Das Element an-1 befindet sich bereits an der richtigen Position; somit wird auch a sortiert. Folgendes Bild 2 veranschaulicht diesen Fall.
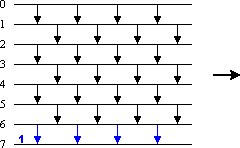
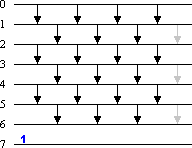
Bild 2: Fall 1
2. Fall: Ist an-1 = 0, so führen alle Vergleicher, auf die diese Null trifft, eine Vertauschung durch (auch wenn ein Vergleicher in Wirklichkeit keine Vertauschung durchführt, weil das andere zu vergleichende Element auch eine Null ist, ist das Ergebnis dasselbe). Die entsprechenden Vergleicher können somit durch sich überkreuzende Linien ersetzt werden (Bild 3).
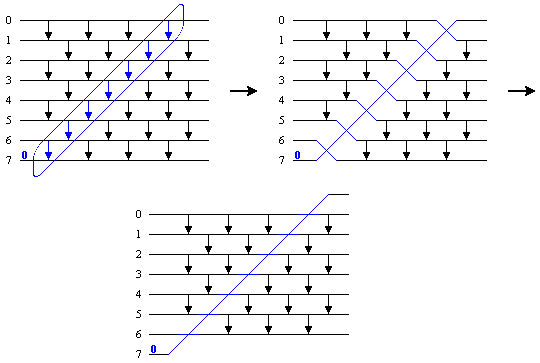
Bild 3: Fall 2
Es verbleibt ein Odd-even-Transposition-Vergleichernetz für n-1 Elemente, das nach Induktionsannahme die Folge a0, ..., an-2 sortiert. Es wird von einer Leitung überkreuzt, die an-1 = 0 an die oberste Position bringt; somit wird auch a sortiert. Damit ist die Behauptung für beliebiges n ∈ ℕ bewiesen.
Es ist auch möglich, Odd-even Transposition Sort durch Umformung in Bubblesort zu beweisen.
Literatur
[Knu 73] D.E. Knuth: The Art of Computer Programming, Vol. 3 - Sorting and Searching. Addison-Wesley (1973)
[Lan 12] H.W. Lang: Algorithmen in Java. 3. Auflage, Oldenbourg (2012)
Das Verfahren Odd-even-Transposition Sort sowie andere Sortiernetze wie Bitonic Sort oder Odd-even Mergesort finden Sie auch in meinem Buch über Algorithmen.
Weitere Themen des Buches: Sortieren, Textsuche, Graphenalgorithmen, Arithmetik, Codierung, Kryptografie, parallele Sortieralgorithmen.
Themen des Buches: Sortieren, Textsuche, Graphenalgorithmen, Arithmetik, Codierung, Kryptografie, parallele Sortieralgorithmen.
Weiter mit: [Odd-even Mergesort] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 21.10.2001 Updated: 07.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden
