Sortieren auf zweidimensionalen Prozessorfeldern
Algorithmus 4-Way-Mergesort
Ein besonders einfaches und gut zu implementierendes Verfahren ist das Verfahren 4-way-Mergesort von Schimmler [Schi 87].
Verfahren
Definition: Ein m×n-Feld von Daten heißt grobsortiert, wenn jedes Element bereits in der richtigen Zeile steht (sodass also anschließendes Sortieren der Zeilen ausreicht, um das Feld vollständig zu sortieren).
Der Algorithmus 4-way-Mergesort beruht auf einem Merge-Verfahren, welches vier grobsortierte k/2×k/2-Felder zu einem grobsortierten k×k-Feld vereinigt.
Prozedur 4-way-merge(k)
Eingabe:
k×k-Feld, dessen vier k/2×k/2-Felder grobsortiert sind
Ausgabe:
Das grobsortierte k×k-Feld
Methode:
- Sortieren der Zeilen der Teilfelder:
- aufsteigend in den oberen Teilfeldern,
- absteigend in den unteren Teilfeldern;
- Sortieren der Spalten;
- Sortieren der Zeilen:
- ungerade Zeilen aufsteigend,
- gerade Zeilen absteigend;
- Sortieren der Spalten;
Die Korrektheit der Prozedur 4-way-merge kann in sehr anschaulicher Weise mithilfe des 0-1-Prinzips gezeigt werden. (Das 0-1-Prinzip gilt auch für den Begriff "grobsortiert", da durch anschließendes Sortieren der Zeilen der sortierte Zustand herbeigeführt werden kann.)
Ausgangssituation ist ein nur mit Nullen und Einsen belegtes Feld, dessen vier Teilfelder grobsortiert sind. In Bild 1a ist diese Situation dargestellt (Nullen sind weiß dargestellt, Einsen grau).
Nach dem Sortieren der Zeilen der Teilfelder in Schritt 1 ergibt sich Bild 1b.
Nach dem Sortieren der Spalten in Schritt 2 ergeben sich zwei grobsortierte k×k/2-Felder (Bild 1c).
Nach dem gegenläufigen Sortieren der Zeilen in Schritt 3 sind zwei unterschiedliche Situationen möglich: entweder befinden sich die "gemischten" Halbzeilen (d.h. Halbzeilen in denen sowohl Nullen als auch Einsen vorkommen) aus Bild 1c in verschiedenen Hälften (Bild 1d) oder in der gleichen Hälfte des Feldes (in Bild 1e in der rechten Hälfte). Dies hängt von der Anzahl der vollständig mit Einsen belegten Halbzeilen ab.
In beiden Fällen jedoch führt das Sortieren der Spalten in Schritt 4 zu der in Bild 1f gezeigten Situation, nämlich einem grobsortierten k×k-Feld.
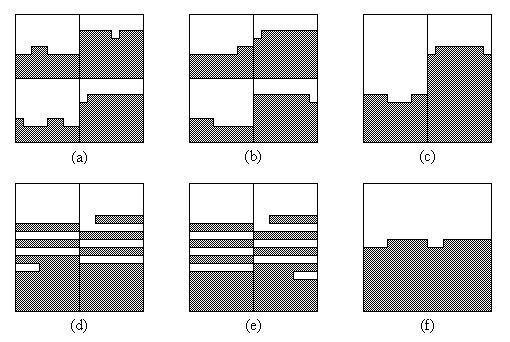
Bild 1: Beweis der Korrektheit der Prozedur 4-way-merge mit Hilfe des 0-1-Prinzips
Durch rekursive Anwendung der Prozedur 4-way-merge kann ein völlig unsortiertes Feld grobsortiert werden:
Prozedur roughsort(k)
Eingabe:
Unsortiertes k×k-Feld
Ausgabe:
Das grobsortierte k×k-Feld
Methode:
- wenn k > 1 dann
- roughsort(k/2) auf die vier k/2×k/2-Teilfelder anwenden;
- 4-way-merge(k);
Ein n×n-Feld wird sortiert, indem es zunächst grobsortiert wird und dann die Zeilen sortiert werden:
Algorithmus 4-way-Mergesort(n)
Eingabe:
Unsortiertes n×n-Feld
Ausgabe:
Das sortierte n×n-Feld
Methode:
- roughsort(n);
- Zeilen sortieren;
Dem 0-1-Prinzip zufolge sortiert das Verfahren jeden beliebigen Datensatz, da es nach obiger Argumentation alle 0-1-Datensätze sortiert.
Analyse
Die Analyse der Prozedur 4-way-merge ergibt folgendes, wenn das Sortieren einer Zeile bzw. Spalte der Länge k mit Odd-even Transposition Sort k Schritte dauert:
| Schritt 1: | k/2 | Schritte | ||
| Schritt 2: | k | Schritte | ||
| Schritt 3: | k | Schritte | ||
| Schritt 4: | k/2 | Schritte | ||
| insgesamt: | 3k | Schritte |
In Schritt 4 sind nur k/2 Schritte von Odd-even Transposition Sort erforderlich, da jede Spalte aus zwei ineinander verschränkten sortierten Teilfolgen besteht.
Der Algorithmus 4-way-Mergesort benötigt für die rekursive Ausführung von 4-way-merge im Aufruf von roughsort insgesamt 3n + 3n/2 + 3n/4 + ... + 3 ≤ 6n Schritte. Für das anschließende Sortieren der Zeilen sind noch einmal n Schritte erforderlich, sodass sich insgesamt ergibt:
T(n) ≤ 7n
Zusammenfassung
Der vorgestellte Algorithmus 4-way-Mergesort zum Sortieren eines n×n-Feldes hat die gleiche asymptotische Zeitkomplexität wie der Algorithmus von Thompson-Kung [TK 77], nämlich O(n). Hinsichtlich der Konstanten ist er jedoch um einen Faktor von gut 2 schlechter. Die Qualität des Algorithmus liegt in seiner Einfachheit bei gleichzeitiger asymptotischer Optimalität.
Eine Implementierung des Algorithmus auf einem befehlssystolischen Feld ist in [Schi 87] sowie in [Lan 90] angegeben.
Literatur
[Lan 90] H.W. Lang: Das befehlssystolische Prozessorfeld -- Architektur und Programmierung. Dissertation, Christian-Albrechts-Universität Kiel (1990)
[Schi 87] M. Schimmler: Fast Sorting on the Instruction Systolic Array. Bericht Nr. 8709, Institut für Informatik, Christian-Albrechts-Universität Kiel (1987)
[TK 77] C.D. Thompson, H.T. Kung: Sorting on a Mesh-Connected Parallel Computer. Communications of the ACM, 20, 4, 263-271 (1977)
Weiter mit: [Sortierverfahren Rotatesort] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 01.03.2000 Updated: 07.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden