Sortieren auf zweidimensionalen Prozessorfeldern
LS3-Sort
Ein sehr einfaches und gut zu implementierendes Verfahren zum Sortieren auf einem zweidimensionalen Prozessorfeld ist das Verfahren LS3-Sort von Lang, Schimmler, Schmeck und Schröder [LSSS 85].
Verfahren
Der Algorithmus LS3-Sort beruht auf einem Merge-Verfahren, welches vier sortierte k/2×k/2-Felder zu einem sortierten k×k-Feld vereinigt. Sortierrichtung ist die Schlangenlinie. Als Grundoperationen werden die Operationen shuffle und oets benutzt.
shuffle
Ein professioneller Kartenspieler mischt einen Stoß Spielkarten, indem er die erste und die zweite Hälfte reißverschlussartig ineinander gleiten lässt. Die englische Bezeichnung hierfür ist perfect shuffle oder kurz shuffle. Sie steht für folgende Permutation, hier dargestellt für n = 8 Elemente:
| 0 1 2 3 4 5 6 7 |
| 0 4 1 5 2 6 3 7 |
Auf Prozessorfeldern kann die Permutation shuffle durch ein "Dreieck" von Vertauschungen zwischen Nachbarelementen hergestellt werden:
| 0 1 2 3 4 5 6 7 |
| ⟷ |
| ⟷ ⟷ |
| ⟷ ⟷ ⟷ |
| 0 4 1 5 2 6 3 7 |
oets
Die Operation oets steht für einen Schritt von Odd-even Transposition Sort. Bei einem Even-Schritt werden alle Elemente, die sich an geraden Positionen der Sortierreihenfolge befinden, mit ihren rechten Nachbarelementen verglichen und gegebenenfalls vertauscht, bei einem Odd-Schritt alle ungeraden Elemente. Odd- und Even-Schritte werden abwechselnd angewandt.
Prozedur ls3Merge(k)
Eingabe:
k×k-Feld, dessen vier k/2×k/2-Teilfelder in Schlangenlinie sortiert sind
Ausgabe:
Das in Schlangenlinie sortierte k×k-Feld
Methode:
- shuffle in den Zeilen
- Sortieren der Doppelspalten (in Schlangenlinie)
- 2k oets-Schritte auf der Schlangenlinie
Die Korrektheit der Prozedur ls3Merge wird mithilfe des 0-1-Prinzips gezeigt.
Ausgangssituation ist ein nur mit Nullen und Einsen belegtes Feld, dessen vier Teilfelder sortiert sind. In Bild 1a ist diese Situation dargestellt (Nullen sind weiß dargestellt, Einsen grau). Jedes der Teilfelder enthält eine gewisse Anzahl von vollen Zeilen (a, b, c bzw. d) sowie möglicherweise eine angefangene Zeile.
Nach der Operation shuffle in Schritt 1 ergibt sich Bild 1b. In jeder Doppelspalte befinden sich a + b + c + d Einsen aus den vollen Zeilen plus maximal vier weitere Einsen aus den angefangenen Zeilen.
Fall 1: a + b + c + d gerade
Nach dem Sortieren der Doppelspalten in Schritt 2 ergibt sich Bild 1c. Die Einsen aus den vollen Zeilen ergeben (a+b+c+d)/2 volle Zeilen. Zusätzlich sind in jeder Doppelspalte maximal vier Einsen aus den angefangenen Zeilen. Diese bilden eine aus maximal zwei Zeilen bestehende unsortierte Zone.
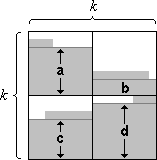
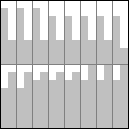
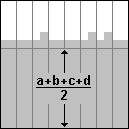
Bild 1: Beweis der Korrektheit der Prozedur ls3Merge
Fall 2: a + b + c + d ungerade
Ist a + b + c + d ungerade, so bilden die Einsen aus den vollen Zeilen in jeder Doppelspalte eine Stufe (Bild 2). Wenn jetzt in einer Doppelspalte 0 und in einer anderen 4 Einsen aus den angefangenen Zeilen hinzukämen, so ergäbe sich eine aus drei Zeilen bestehende unsortierte Zone.
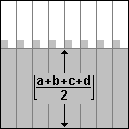
Bild 2: Einsen aus den vollen Zeilen, wenn a+b+c+d ungerade
Dies ist jedoch nur dann möglich, wenn alle angefangenen Zeilen auf derselben Seite anfangen (z.B. alle links oder alle rechts). Bei der Sortierrichtung in Schlangenlinien bedeutet dies aber, dass die Zahlen a, b, c, d alle gerade oder alle ungerade sind. Dann aber kann ihre Summe nicht ungerade sein.
Wenn a + b + c + d ungerade ist, kommen also in jeder Doppelspalte entweder mindestens eine Eins oder höchstens drei Einsen hinzu. Somit umfasst die unsortierte Zone auch in diesem Fall höchstens zwei Zeilen.
In Schritt 3 der Prozedur wird die aus maximal zwei Zeilen, d.h. aus maximal 2k Elementen bestehende unsortierte Zone schließlich sortiert. Hierfür genügen 2k oets-Schritte.
Durch rekursive Anwendung der Prozedur ls3Merge kann ein völlig unsortiertes Feld sortiert werden:
Algorithmus ls3Sort(n)
Eingabe:
Unsortiertes n×n-Feld
Ausgabe:
Das sortierte n×n-Feld
Methode:
- wenn n > 1 dann
- wende ls3Sort(n/2) rekursiv auf die vier n/2×n/2-Teilfelder an
- ls3Merge(n)
Analyse
Die Analyse der Prozedur ls3Merge(k) ergibt folgende Anzahl von Operationen:
| Schritt 1: | k/2 | |
| Schritt 2: | 2k | |
| Schritt 3: | 2k | |
| insgesamt: | 4.5k |
Der Algorithmus LS3-Sort benötigt T(n) = 4.5(n + n/2 + n/4 + ... + 2) Operationen; es gilt somit
T(n) ≤ 9n
In [LSSS 85] wird gezeigt, dass sich die Zeitkomplexität von LS3-Sort noch auf 7n verringern lässt, indem u.a. die Doppelspalten schneller als in 2k Schritten sortiert werden.
Simulation
Das folgende Applet zeigt den Ablauf von LS3-Sort mit einem 32×32-Feld von Nullen und Einsen. Zur besseren Anschaulichkeit werden die Operationen sequentiell angezeigt, auch wenn sie auf einem zweidimensionalen Prozessorfeld parallel ablaufen könnten.
(Java-Applet zur Simulation von LS3-Sort)
Zusammenfassung
Der vorgestellte Algorithmus LS3-Sort zum Sortieren eines n×n-Feldes hat die gleiche asymptotische Zeitkomplexität wie der Algorithmus von Thompson-Kung [TK 77], nämlich O(n). Hinsichtlich der Konstanten ist er jedoch um einen Faktor von gut 2 schlechter. Die Qualität des Algorithmus liegt in seiner Einfachheit bei gleichzeitiger asymptotischer Optimalität.
Literatur
[LSSS 85] H.W. Lang, M. Schimmler, H. Schmeck, H. Schröder: Systolic Sorting on a Mesh-Connected Network. IEEE Transactions on Computers C-34, 7, 652-658 (1985)
[TK 77] C.D. Thompson, H.T. Kung: Sorting on a Mesh-Connected Parallel Computer. Communications of the ACM, 20, 4, 263-271 (1977)
[Lan 12] H.W. Lang: Algorithmen in Java. 3. Auflage, Oldenbourg (2012)
Das Verfahren LS3-Sort finden Sie auch in meinem Buch über Algorithmen.
Weitere Themen des Buches: Sortieren, Textsuche, Parsen und Übersetzen, Graphenalgorithmen, Arithmetik, Codierung, Kryptografie.
Themen des Buches: Sortieren, Textsuche, Parsen und Übersetzen, Graphenalgorithmen, Arithmetik, Codierung, Kryptografie.
Weiter mit: [Sortierverfahren 4-way Mergesort] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 20.07.2001 Updated: 07.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden
