Sortieren auf zweidimensionalen Prozessorfeldern
Rotatesort
Ein interessantes und gut zu implementierendes Sortierverfahren für ein zweidimensionales Prozessorfeld ist das Verfahren Rotatesort von Marberg und Gafni [MG 88]. Es zeichnet sich dadurch aus, dass es nur eine konstante Zahl von Phasen umfasst, wobei eine Phase eine maximale Zeilen- bzw. Spaltenoperation ist.
Verfahren
Das n×n-Feld wird in senkrechte Scheiben, waagerechte Scheiben und in Blöcke unterteilt. Eine senkrechte Scheibe ist (siehe Bild 1) ein n× n-Teilfeld, eine waagerechte Scheibe ist ein
n-Teilfeld, eine waagerechte Scheibe ist ein  n×n-Teilfeld, und ein Block ist ein
n×n-Teilfeld, und ein Block ist ein  n×
n× n-Teilfeld.
n-Teilfeld.
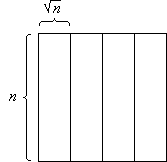
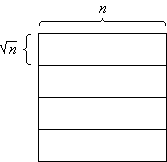
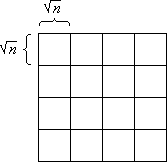
Bild 1: Senkrechte Scheiben (a), waagerechte Scheiben (b) und Blöcke (c)
Der Algorithmus Rotatesort greift auf drei Operationen zurück: balance, unblock und shear.
balance
Die Operation balance wird auf eine senkrechte Scheibe angewandt.
- Sortieren der Spalten
- Rotieren der Zeilen
- Sortieren der Spalten
Jede Zeile i wird um i mod  n rotiert.
n rotiert.
unblock
Die Operation unblock wird auf das ganze Feld angewandt. Sie verteilt die n Elemente jedes Blocks über die ganze Breite des Feldes.
- Rotieren der Zeilen
- Sortieren der Spalten
Jede Zeile i wird um i· n mod n rotiert.
n mod n rotiert.
shear
Die Operation shear wird auf das ganze Feld angewendet.
- Gegenläufiges Sortieren der Zeilen
- Sortieren der Spalten
Gegenläufiges Sortieren bedeutet, dass jede Zeile i aufsteigend sortiert wird, wenn i gerade ist, und absteigend, wenn i ungerade ist.
Algorithmus Rotatesort
Eingabe:
Unsortiertes n×n-Feld von Daten
Ausgabe:
Das sortierte n×n-Feld
Methode:
- balance auf jede senkrechte Scheibe anwenden;
- unblock;
- balance auf jede waagerechte Scheibe anwenden;
- unblock;
- shear dreimal anwenden;
- Sortieren der Zeilen;
In Schritt 3 wird balance auf die waagerechten Scheiben angewendet, als ob es auf der Seite liegende senkrechte Scheiben wären.
Korrektheit
Die Korrektheit des Algorithmus Rotatesort wird wiederum mit Hilfe des 0-1-Prinzips gezeigt. In den folgenden Abbildungen sind Nullen weiß und Einsen grau dargestellt.
Definition: Ein r×s-Teilfeld heißt einfarbig, wenn es nur aus Nullen oder nur aus Einsen besteht, anderenfalls heißt es gemischt.
Insbesondere bezieht sich diese Definition auf Zeilen und auf Blöcke. Eine gemischte Zeile enthält also sowohl Nullen als auch Einsen, eine einfarbige Zeile enthält entweder nur Nullen oder nur Einsen.
Schritt 1
Die Operation balance, angewandt auf eine senkrechten Scheibe, reduziert die Anzahl der gemischten Zeilen in der Scheibe auf maximal  n. Denn jede Spalte der Scheibe wird, nachdem sie in Teilschritt (a) sortiert worden ist, in Teilschritt (b) durch das Rotieren gleichmäßig auf alle Spalten verteilt. Nach dem Sortieren in Teilschritt (c) sind aus den Einsen der Spalte eine gewisse Anzahl voller Zeilen sowie möglicherweise eine angefangene, also gemischte Zeile geworden (Bild 2).
n. Denn jede Spalte der Scheibe wird, nachdem sie in Teilschritt (a) sortiert worden ist, in Teilschritt (b) durch das Rotieren gleichmäßig auf alle Spalten verteilt. Nach dem Sortieren in Teilschritt (c) sind aus den Einsen der Spalte eine gewisse Anzahl voller Zeilen sowie möglicherweise eine angefangene, also gemischte Zeile geworden (Bild 2).
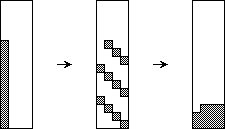
Bild 2: Verteilung einer Spalte auf eine senkrechte Scheibe durch balance
Da jede der  n Spalten der Scheibe eine gemischte Zeile erzeugen kann, ergeben sich maximal
n Spalten der Scheibe eine gemischte Zeile erzeugen kann, ergeben sich maximal  n gemischte Zeilen in der Scheibe. Durch die gemischten Zeilen können maximal zwei Blöcke betroffen sein.
n gemischte Zeilen in der Scheibe. Durch die gemischten Zeilen können maximal zwei Blöcke betroffen sein.
Insgesamt also verbleiben nach Schritt 1 maximal 2 n gemischte Blöcke. Diese Situation ist in Bild 3 dargestellt.
n gemischte Blöcke. Diese Situation ist in Bild 3 dargestellt.
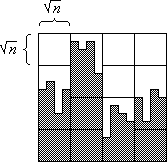
Bild 3: Situation nach Schritt 1
Schritt 2
Die Operation unblock verteilt durch das Rotieren in Teilschritt (a) jeden Block auf alle Spalten (Bild 4).
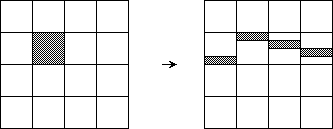
Bild 4: Rotation in der Operation unblock
Nach dem Sortieren der Spalten in Teilschritt (b) hat jeder einfarbige Block eine einfarbige Zeile erzeugt, jeder gemischte Block eine gemischte Zeile. Es verbleiben also nach Schritt 2 maximal 2 n gemischte Zeilen, die von den gemischten Blöcken herrühren.
n gemischte Zeilen, die von den gemischten Blöcken herrühren.
Schritt 3
Von den maximal 2 n gemischten Zeilen sind maximal drei waagerechte Scheiben betroffen. Nach Schritt 3 (balance angewendet auf die waagerechten Scheiben) verbleiben maximal 6 gemischte Blöcke (Bild 5).
n gemischten Zeilen sind maximal drei waagerechte Scheiben betroffen. Nach Schritt 3 (balance angewendet auf die waagerechten Scheiben) verbleiben maximal 6 gemischte Blöcke (Bild 5).
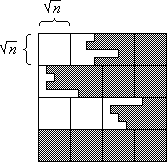
Bild 5: Situation nach Schritt 3
Schritt 4
Nach Schritt 4 (unblock) sind aus den maximal 6 gemischten Blöcken maximal 6 gemischte Zeilen geworden.
Schritt 5
Die Operation shear reduziert je zwei gemischte Zeilen zu maximal einer gemischten Zeile. Nach dem gegenläufigen Sortieren der Zeilen beginnen die geraden Zeilen mit Nullen und enden mit Einsen, bei den ungeraden Zeilen ist es umgekehrt. Nach dem Sortieren der Spalten ist eine einfarbige Zeile von Nullen entstanden (Bild 6 a) oder eine einfarbige Zeile von Einsen (Bild 6 b).
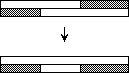
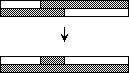
Bild 6: Operation shear
Diese Technik wird auch in dem Algorithmus Shearsort [SchS 89] angewendet. Auch im Algorithmus 4-way-Mergesort [Schi 87] kommt dieser Schritt vor.
Durch die shear-Operation halbiert sich insgesamt die Anzahl der gemischten Zeilen. Durch dreimaliges Anwenden von shear in Schritt 5 reduzieren sich die 6 gemischten Zeilen zu einer gemischten Zeile.
Schritt 6
In Schritt 6 schließlich wird die letzte verbliebene gemischte Zeile sortiert.
Dem 0-1-Prinzip zufolge sortiert das Verfahren jeden beliebigen Datensatz, da es nach obiger Argumentation alle 0-1-Datensätze sortiert.
Analyse
Die Analyse des Algorithmus Rotatesort ergibt Folgendes, wenn das Sortieren oder Rotieren einer Zeile bzw. Spalte vorläufig als eine Phase gezählt wird:
| Schritt 1: | balance | 3 | Phasen | |||
| Schritt 2: | unblock | 2 | Phasen | |||
| Schritt 3: | balance | 3 | Phasen | |||
| Schritt 4: | unblock | 2 | Phasen | |||
| Schritt 5: | 3 × shear | 6 | Phasen | |||
| Schritt 6: | Zeilen sortieren | 1 | Phase | |||
| insgesamt: | 17 | Phasen |
Da eine Phase eine maximale Zeilen- bzw. Spaltenoperation ist, verringert sich die Gesamtanzahl auf 16, denn die Teilschritte 3c und 4a können zu einer Zeilenoperation zusammengefasst werden.
Wird das Sortieren einer Zeile oder Spalte mit Odd-even Transposition Sort durchgeführt, sowie das Rotieren ebenfalls mit lokalen Vertauschungen, so erfordert jede Phase höchstens n Schritte. Der Algorithmus liegt also in O(n), wobei die Konstante 17 nicht so sehr gut ist. So hat z.B. LS3-Sort eine Konstante von 7. Die untere Schranke liegt bei 3; sie wird vom Algorithmus von Thompson-Kung [TK 77] und vom Algorithmus von Schnorr-Shamir auch erreicht (bei Vernachlässigung von Termen geringerer Ordnung).
Eine genauere Analyse des Algorithmus ergibt immerhin eine Konstante von 10.
In Schritt 1 und Schritt 3 brauchen die Rotierphasen nicht mitgezählt werden, da sie nur  n Schritte benötigen. Die Rotierphase von unblock lässt sich in n/2 Schritten realisieren, indem eine Rechtsrotation um k > n/2 Positionen durch eine Linksrotation um n-k < n/2 Positionen ersetzt wird. In Schritt 4 entstehen bei unblock nur 3
n Schritte benötigen. Die Rotierphase von unblock lässt sich in n/2 Schritten realisieren, indem eine Rechtsrotation um k > n/2 Positionen durch eine Linksrotation um n-k < n/2 Positionen ersetzt wird. In Schritt 4 entstehen bei unblock nur 3 n gemischte Zeilen; für das Sortieren der Spalten reichen entsprechend viele Schritte von Odd-even Transposition Sort aus. Ferner erfordert shear für das Sortieren der Spalten nur konstant viele Schritte von Odd-even Transposition Sort, da nur noch konstant viele gemischte Zeilen vorhanden sind. Diese Phasen brauchen also auch nicht mitgezählt zu werden.
n gemischte Zeilen; für das Sortieren der Spalten reichen entsprechend viele Schritte von Odd-even Transposition Sort aus. Ferner erfordert shear für das Sortieren der Spalten nur konstant viele Schritte von Odd-even Transposition Sort, da nur noch konstant viele gemischte Zeilen vorhanden sind. Diese Phasen brauchen also auch nicht mitgezählt zu werden.
Satz: Rotatesort benötigt höchstens 10n + O( n) Schritte.
n) Schritte.
Zusammenfassung
Der vorgestellte Algorithmus Rotatesort zum Sortieren eines n×n-Feldes hat die gleiche asymptotische Zeitkomplexität wie der Algorithmus von Thompson-Kung [TK 77], nämlich O(n). Hinsichtlich der Konstanten ist er jedoch um einen Faktor von gut 3 schlechter.
Literatur
[MG 88] J.M. Marberg, E. Gafni: Sorting in Constant Number of Row and Column Phases on a Mesh. Algorithmica 3, 561-572 (1988)
[Schi 87] M. Schimmler: Fast Sorting on the Instruction Systolic Array. Bericht Nr. 8709, Institut für Informatik, Christian-Albrechts-Universität Kiel (1987)
[SchS 89] I.D. Scherson, S. Sen: Parallel sorting in two-dimensional VLSI models of computation. IEEE Transactions on Computers C-38, 2, 238-249 (1989)
[TK 77] C.D. Thompson, H.T. Kung: Sorting on a Mesh-Connected Parallel Computer. Communications of the ACM, 20, 4, 263-271 (1977)
[Lan 12] H.W. Lang: Algorithmen in Java. 3. Auflage, Oldenbourg (2012)
Das Verfahren Rotatesort finden Sie auch in meinem Buch über Algorithmen.
Weitere Themen des Buches: Sortieren, Textsuche, Parsen und Übersetzen, Graphenalgorithmen, Arithmetik, Codierung, Kryptografie.
Themen des Buches: Sortieren, Textsuche, Parsen und Übersetzen, Graphenalgorithmen, Arithmetik, Codierung, Kryptografie.
Weiter mit: [Sortierverfahren von Schnorr-Shamir] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 06.03.2001 Updated: 07.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden
