Sortiernetze
Sortiernetze
Sortiernetze sind Spezialfälle von Sortierverfahren im Allgemeinen. Sie zeichnen sich dadurch aus, dass die Vergleiche datenunabhängig durchgeführt werden. Die einzige verwendete Art von Operation ist der Vergleichs-Austausch-Schritt zwischen zwei Datenelementen: Wenn ai größer als aj ist, dann vertausche ai und aj.
Sortierverfahren dieser Art lassen sich leicht parallelisieren und gegebenenfalls in Hardware realisieren.
Definition: Sei J = {0, ..., n-1} eine Indexmenge und A eine Menge von Daten mit einer Ordnungsrelation ≤. Eine Datenfolge ist eine Abbildung a : J → A, also eine Folge der Länge n von Daten. Die Menge aller Datenfolgen der Länge n über A bezeichnen wir mit An.
Die folgende Definition behandelt den einfachsten Fall des aufsteigenden Sortierens von Datenfolgen.
Definition: Das Sortierproblem besteht darin, eine beliebige Datenfolge a0, ..., an-1, ai ∈ A so zu einer Folge aφ(0), ..., aφ(n-1) umzuordnen, dass gilt:
aφ(i) ≤ aφ(j) für i < j.
Hierbei ist φ eine Permutation der Indexmenge J = {0, ..., n-1}.
Später werden wir im Zusammenhang mit Sortierverfahren auf zweidimensionalen Prozessorfeldern diese Definition verallgemeinern und die Indexmenge J = {0, ..., n-1} × {0, ..., n-1} sowie eine Sortierrichtung ρ : J → {0, ..., |J|-1} einführen.
Vergleichernetz
Vergleichernetze wurden informell in [Knu 73] und für den Fall J = {0, ..., n-1} eingeführt. Ein Vergleicher [i:j] bringt das i-te und das j-te Datenelement einer Folge in aufsteigende Reihenfolge. Formal ist ein solcher Vergleicher eine Abbildung, die auf die Datenfolge a ∈ An angewandt wird:
Definition: Ein Vergleicher ist eine Abbildung
[i:j] : An → An, i, j ∈ {0, ..., n-1}
mit
[i:j](a)i = min(ai, aj)
[i:j](a)j = max(ai, aj)
[i:j](a)k = ak für alle k mit k ≠ i, k ≠ j
für alle a ∈ An.
Vergleicher werden grafisch als Pfeile dargestellt (Bild 1). Dabei ist die Vorstellung, dass die Datenfolge von links nach rechts entlang der waagerechten Linien wandert. Elemente der Datenfolge, die dabei auf einen Vergleicher treffen, werden in Pfeilrichtung sortiert. In Bild 1 wandert die Datenfolge 6 8 5 1 an den Linien entlang und trifft dabei nacheinander auf die zwei Vergleicher [1:3] und [2:1].
Bild 1: Umordnen einer Datenfolge durch Vergleicher
Wie in Bild 1 angedeutet, lassen sich Vergleicher zu Vergleichernetzen zusammenschalten.
Definition: Ein Vergleichernetz N ist eine Hintereinanderausführung von Vergleichern:
N = [i1:j1]· ...· [im:jm] , m ∈ ℕ
Bild 2 zeigt als Beispiel das Vergleichernetz
N = [0:2] · [1:3] · [0:1] · [2:3]
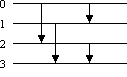
Bild 2: Vergleichernetz N
Bei einem Vergleichernetz kommt es im Allgemeinen auf die Reihenfolge der Vergleicher an. Wenn jedoch zwei aufeinander folgende Vergleicher keine waagerechte Linie gemeinsam haben, wie zum Beispiel in Bild 2 die Vergleicher [0:2] und [1:3] oder die Vergleicher [0:1] und [2:3], so können sie offenbar auch in umgekehrter Reihenfolge ausgeführt werden; die von ihnen bewirkte Abbildung bleibt dieselbe.
Definition: Zwei Vergleichernetze N und M sind äquivalent, wenn sie dieselbe Abbildung bewirken, d.h. wenn sie jede Eingabefolge a in jeweils dieselbe Ausgabefolge überführen:
N ≡ M ⇔ ∀a : N(a) = M(a)
Definition: Zwei Vergleicher [i:j] und [k:l] heißen unabhängig, wenn sie keine Linie gemeinsam haben, d.h. wenn i, j, k, l paarweise verschieden sind.
Satz: Für zwei unabhängige Vergleicher [i:j] und [k:l] gilt
[i:j] · [k:l] ≡ [k:l] · [i:j]
Definition: Eine Vergleicherstufe S ist eine Hintereinanderausführung von paarweise unabhängigen Vergleichern
S = [i1:j1]· ...· [ir:jr] , r ∈ ℕ
Die Vergleicher innerhalb einer Vergleicherstufe können in beliebiger Reihenfolge, oder aber auch parallel ausgeführt werden. Das Vergleichernetz in Bild 2 besteht aus zwei Vergleicherstufen.
Definition: Ein Vergleicher [i:j] heißt Standard-Vergleicher, wenn er von oben nach unten gerichtet ist, wenn also i < j ist. Ein Vergleichernetz heißt Standard-Vergleichernetz, wenn alle Vergleicher von oben nach unten gerichtet sind, d.h. wenn alle Vergleicher Standard-Vergleicher sind.
Definition: Ein Vergleicher heißt primitiv, wenn er zwischen benachbarten waagerechten Linien liegt und von oben nach unten gerichtet ist, d.h. wenn er von der Form [i-1: i] ist. Ein Vergleichernetz heißt primitiv, wenn alle seine Vergleicher primitiv sind.
Bei primitiven Vergleichernetzen bezeichnen wir einen Vergleicher [i-1: i] nur durch die Zahl i. Ein primitives Vergleichernetz entspricht damit einer Folge von Zahlen aus der Menge {1, ..., n-1}.
Beispiel: Folgendes Vergleichernetz N ist primitiv (Bild 3). Es kann daher durch N = 1 2 4 1 3 bezeichnet werden.
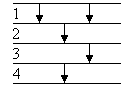
Bild 3: Primitives Vergleichernetz
Sortiernetz
Definition: Ein Sortiernetz ist ein Vergleichernetz, das alle Eingabefolgen sortiert.
Das Vergleichernetz aus Bild 2 ist kein Sortiernetz, weil es z.B. die Folge 3 1 4 2 nicht sortiert.
Die Frage, ob ein beliebig vorgegebenes Vergleichernetz ein Sortiernetz ist oder nicht, ist im Allgemeinen nicht leicht zu beantworten, das Problem ist NP-schwer. Unabhängig davon lassen sich natürlich Sortiernetze systematisch konstruieren und beweisen.
Beispiele hierfür sind die in den folgenden Seiten angegebenen Sortierverfahren Bubblesort, Odd-even Transposition Sort, Bitonic Sort und Odd-even Mergesort, ferner auch Shellsort. Diese lassen sich als Sortiernetze realisieren.
Bubblesort und Odd-even Transposition Sort sind primitive Sortiernetze, d.h. Vergleiche finden nur zwischen benachbarten Elementen der Datenfolge statt. Primitive Sortiernetze benötigen immer Ω(n2) Vergleicher zum Sortieren von n Daten. Die Bedeutung dieser Verfahren liegt darin, dass sie sich sehr gut für eine parallele Implementierung in Hardware oder auf Prozessorfeldern eignen, da die Datenkommunikation lokal ist.
Mit O(n·log(n)2) Vergleichern wesentlich effizientere, wenn auch nicht optimale Sortiernetze sind Bitonic Sort, Odd-even Mergesort und Shellsort. Ein mit einer Komplexität von O(n·log(n)) asymptotisch optimales Sortiernetz existiert [AKS 83]; es ist jedoch aufgrund seiner hohen Konstanten erst für (unrealistische) Problemgrößen von über 21000 besser als Bitonic Sort.
In der folgenden Tabelle ist die Komplexität der erwähnten Sortiernetze zusammenfassend dargestellt. Die Anzahl der Vergleicherstufen entspricht der Zeitkomplexität, die Anzahl der Vergleicher dem Hardwareaufwand bei paralleler Implementierung. Bei sequentieller Implementierung entspricht die Anzahl der Vergleicher der Zeitkomplexität.
| Vergleicherstufen | Vergleicher | |||
| Bubblesort | Θ(n) | Θ(n2) | ||
| Odd-even Transposition Sort | Θ(n) | Θ(n2) | ||
| Bitonic Sort | Θ(log(n)2) | Θ(n·log(n)2) | ||
| Odd-even Mergesort | Θ(log(n)2) | Θ(n·log(n)2) | ||
| Shellsort | Θ(log(n)2) | Θ(n·log(n)2) |
Literatur
[AKS 83] M. Ajtai, J. Komlos, E. Szemeredi: An
[Knu 73] D.E. Knuth: The Art of Computer Programming, Vol. 3 - Sorting and Searching. Addison-Wesley (1973)
[Lan 12] H.W. Lang: Algorithmen in Java. 3. Auflage, Oldenbourg (2012)
Ein Kapitel über Sortiernetze finden Sie auch in meinem Buch über Algorithmen.
Weitere
Themen des Buches: Sortieren, Textsuche, Graphenalgorithmen, algorithmische Geometrie, Arithmetik, Codierung, Kryptografie, parallele Sortieralgorithmen.
Weiter mit: [Bubblesort] [0-1-Prinzip] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 05.03.1997 Updated: 07.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden