Sortiernetze

Bubblesort

Bubblesort ist das einfachste Sortierverfahren. Allerdings hat es eine Zeitkomplexität von Θ(n²), damit ist es für größere Datenmengen nicht geeignet. Denn bereits bei einigen zig-tausend Daten ist Bubblesort 1000-mal langsamer als ein schnelles Sortierverfahren wie etwa Mergesort oder Heapsort.

Bubblesort lässt sich als Sortiernetz implementieren.

Der Algorithmus Bubblesort durchläuft Element für Element die zu sortierende Datenfolge. Wird dabei ein Element erreicht, das kleiner als das vorherige Element ist, so wird es mit diesem vertauscht. Dadurch ist das aktuelle Element immer das Maximum aller bisher durchlaufenen Elemente. Ist die Folge zu Ende durchlaufen, steht das größte Element der Folge an letzter Position.

Im nächsten Durchlauf wird das zweitgrößte Element an die vorletzte Position befördert, und so weiter. Besteht die Folge aus n Elementen, so ist die Folge nach n-1 Durchläufen sortiert.

Den eben skizzierten Ablauf gibt das in Bild 1 dargestellte Sortiernetz Bubblesort wieder. Mit der ersten Diagonalen von Vergleichern wird das größte Element an das Ende der Folge befördert. Mit der zweiten Diagonalen wird das zweitgrößte Element an die vorletzte Position befördert usw.

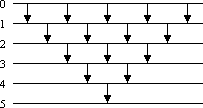
Bild 1: Sortiernetz Bubblesort für n = 6

Die Anzahl der Vergleiche, die Bubblesort zum Sortieren einer Datenfolge der Länge n benötigt, beträgt

n-1 + n-2 + ... + 1 =

n·(n-1)

∈ Θ(n²)

Es folgt die Implementierung als Programm. Die Funktion bubbleSort ist in einer Klasse BubbleSorter gekapselt.

Mit der Anweisung

BubbleSorter s=new BubbleSorter();

wird ein Objekt vom Typ BubbleSorter erzeugt. Mit

s.sort(b);

kann anschließend ein Array b sortiert werden.

public class BubbleSorter
{
    private int[] a;
    private int n;

    // übernimmt ein Array und sortiert es mit Bubblesort
    public void sort(int[] a_)
    {
        a=a_;
        n=a.length;
        bubbleSort();
    }

    // sortiert das Array mit Bubblesort
    private void bubbleSort()
    {
        int i, j;
        for (i=n; i>1; i--)
            for (j=1; j<i; j++)
                if (a[j-1]>a[j])
                    exchange(j-1, j);
    }

    // vertauscht zwei Einträge im Array a
    private void exchange(int i, int j)
    {
        int t=a[i];
        a[i]=a[j];
        a[j]=t;
    }

}    // end class BubbleSorter

Weiter mit: [Selectionsort] oder [up]

H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 20.09.2004 Updated: 07.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden

Sortiernetze

Bubblesort

Idee

Sortiernetz

Analyse

Programm