Sortiernetze
Bitonic Sort
Das Sortierverfahren Bitonic Sort [Bat 68] ist eines der schnellsten Sortiernetze. Bei einem Sortiernetz [Knu 73] [CLRS 01] ist die Reihenfolge der Vergleiche nicht von den Daten abhängig, anders als bei Sortierverfahren wie z.B. Quicksort oder Heapsort. Das Verfahren ist daher besonders für eine Implementierung in Hardware geeignet. Es ist darüber hinaus Grundlage vieler paralleler Sortierverfahren auf zweidimensionalen Prozessorfeldern.
Das Sortiernetz Bitonic Sort enthält Θ(n log(n)2) Vergleicher. Es hat damit dieselbe asymptotische Komplexität wie die Sortiernetze Odd-even Mergesort und Shellsort. Zwar gibt es ein Sortiernetz mit nur O(n log(n)) Vergleichern [AKS 83], dieses ist jedoch aufgrund seiner hohen Konstante für alle praktischen Problemgrößen langsamer als Bitonic Sort.
Im Folgenden wird das Sortiernetz Bitonic Sort auf Basis des 0-1-Prinzips entwickelt. Das 0-1-Prinzip besagt, dass ein Vergleichernetz, das alle Folgen von Nullen und Einsen sortiert, ein Sortiernetz ist, d.h. es sortiert dann auch jede Folge von beliebigen Eingabewerten.
Grundlagen
Definition: Eine Folge a = a0, ..., an-1 mit ai ∈ {0, 1}, i = 0, ..., n-1 heißt 0-1-Folge.
Eine 0-1-Folge heißt bitonisch,1) wenn sie höchstens zwei Wechsel zwischen 0 und 1 enthält, d.h. wenn Zahlen k, m ∈ {1, ..., n} existieren derart dass
a0, ..., ak-1 = 0 , ak, ..., am-1 = 1 , am, ..., an-1 = 0 oder
a0, ..., ak-1 = 1 , ak, ..., am-1 = 0 , am, ..., an-1 = 1.
In folgendem Bild 1 sind verschiedene Beispiele bitonischer 0-1-Folgen schematisch dargestellt (Nullen weiß, Einsen grau):
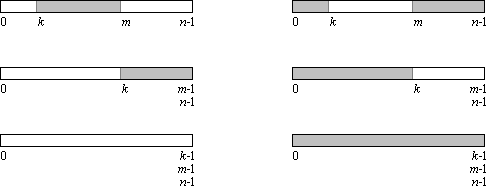
Bild 1: Verschiedene Beispiele bitonischer 0-1-Folgen
Definition: Sei n ∈ ℕ, n gerade. Das Vergleichernetz Bn ist wie folgt definiert:
Bn = [0 : n/2] [1 : n/2+1] ... [n/2-1 : n-1].
Als Beispiel ist in Bild 2 das Vergleichernetz B8 dargestellt.
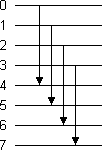
Bild 2: Vergleichernetz B8
Satz: Sei n ∈ ℕ, n gerade und a = a0, ..., an-1 eine bitonische 0-1-Folge. Die Anwendung des Vergleichernetzes Bn auf a ergibt dann
Bn(a) = b0, ..., bn/2-1 c0, ..., cn/2-1,
wobei die bi die kleineren Elemente und die cj die größeren Elemente sind, d.h.
bi≤cj für alle i, j ∈ {0, ..., n/2-1},
und darüber hinaus gilt
b0, ..., bn/2-1 ist bitonische 0-1-Folge und
c0, ..., cn/2-1 ist bitonische 0-1-Folge.
Beweis: Sei a = a0, ..., an-1 eine bitonische 0-1-Folge. Schreibt man a in zwei Zeilen, dann ergibt sich folgendes Bild (Nullen sind wieder weiß, Einsen grau dargestellt). Die Folge beginnt mit Nullen, dann kommen Einsen und dann wieder Nullen (Bild 3a). Oder die Folge beginnt mit Einsen, dann kommen Nullen und dann wieder Einsen (Bild 3b).
Es sind noch eine ganze Reihe anderer Variationen möglich, einige sind in Bild 4 dargestellt. Eine Anwendung des Vergleichernetzes Bn entspricht einem Vergleich zwischen oberer und unterer Zeile; hierdurch wird in allen Fällen die im Satz angegebene Form hergestellt, d.h. alle bi sind kleiner oder gleich allen cj und b ist bitonisch und c ist bitonisch.
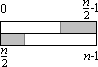
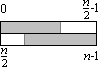
Bild 3: Bitonische 0-1-Folgen (dargestellt jeweils in zwei Zeilen)
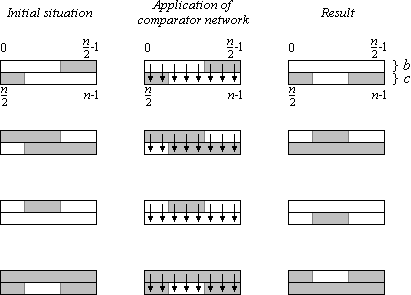
Bild 4: Anwendung des Vergleichernetzes Bn auf bitonische 0-1-Folgen
Sortiernetz BitonicSort
Vergleichernetze Bk für verschiedene Zweierpotenzen k bilden die Bausteine für das Sortiernetz BitonicSort(n). Durch Anwendung des Divide-and-Conquer-Prinzips
werden Vergleichernetze BitonicMerge und BitonicSort konstruiert.
Das Vergleichernetz BitonicMerge(n) sortiert eine bitonische Folge. Aufgrund der Tatsache, dass Bn wiederum bitonische Teilfolgen halber Länge liefert, von denen die erste die kleineren Elemente enthält und die zweite die größeren, lässt es sich rekursiv aufbauen (Bild 5).
Die bitonische Folge, die als Eingabe für BitonicMerge notwendig ist, wird aus einer aufsteigend sortierten und einer absteigend sortierten Hälfte zusammengesetzt. Diese sortierten Hälften werden durch rekursive Anwendung von BitonicSort erzeugt (Bild 6).
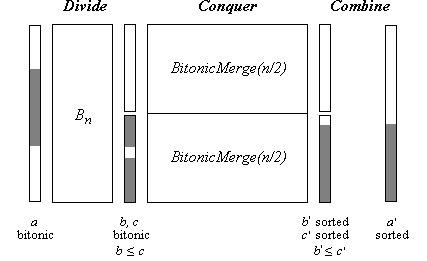
Bild 5: BitonicMerge(n)
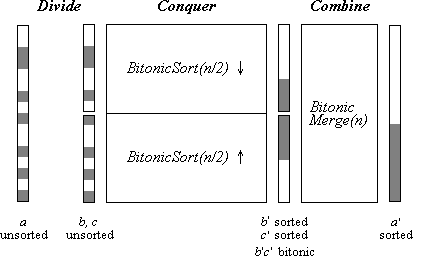
Bild 6: BitonicSort(n)
Im darauf folgenden Bild 7 ist als Beispiel das Sortiernetz BitonicSort(8) dargestellt.
Auf das ganze Vergleichernetz lässt sich das 0-1-Prinzip anwenden: da das Vergleichernetz BitonicSort beliebige 0-1-Folgen sortiert, sortiert es auch jede beliebige andere Folge, ist also ein Sortiernetz.
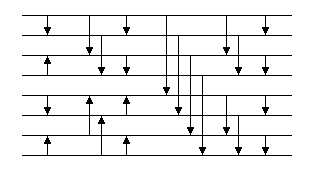
Bild 7: Sortiernetz BitonicSort für n=8
Analyse
Das Vergleichernetz BitonicMerge(n) besteht aus log(n) Vergleicherstufen (so etwa die letzten 3 = log(8) Vergleicherstufen in Bild 7). Die Anzahl der Vergleicherstufen T(n) des gesamten Sortiernetzes BitonicSort(n) ergibt sich also wie folgt:
T(n) = log(n) + T(n/2) sowie
T(1) = 0.
Die Lösung dieser Rekursionsgleichung ist
T(n) = log(n) + log(n)-1 + log(n)-2 + ... + 1 = log(n)·(log(n)+1) / 2.
Jede Vergleicherstufe des Sortiernetzes besteht aus n/2 Vergleichern; insgesamt sind dies also Θ(n log(n)2) Vergleicher.
Programm
Es folgt eine Implementation von Bitonic Sort in Java. Das Verfahren ist in der Klasse BitonicSorter gekapselt. Die Methode sort übergibt das zu sortierende Array an das Array a und ruft bitonicSort auf.
Die Funktion bitonicSort erzeugt zunächst eine bitonische Folge, indem sie die beiden Hälften der Folge gegenläufig sortiert (durch zwei rekursive Aufrufe von bitonicSort). Danach sortiert sie die bitonische Folge durch Aufruf von bitonicMerge.
Die Funktion bitonicMerge sortiert rekursiv eine bitonische Folge a. Die zu sortierende Folge beginnt am Index lo, die Anzahl der Elemente ist n, die Sortierrichtung ist aufsteigend, wenn dir = ASCENDING, sonst absteigend.
Ein Vergleicher wird durch die Funktion compare modelliert. Der Parameter dir gibt die Sortierrichtung an. Die Elemente a[i] und a[j] werden vertauscht, wenn dir = ASCENDING und (a[i] > a[j]) = true oder wenn dir = DESCENDING und (a[i] > a[j]) = false gilt.
Mit den Anweisungen
s.sort(b);
wird ein Objekt vom Typ BitonicSorter erzeugt und anschließend die Methode sort aufgerufen, um ein Array b zu sortieren. Die Länge n des Arrays muss eine Zweierpotenz sein (vgl. Bitonic Sort für beliebiges n).
{
private int[] a;
// sorting direction:
private final static boolean ASCENDING=true, DESCENDING=false;
public void sort(int[] a_)
{
a=a_;
bitonicSort(0, a.length, ASCENDING);
}
private void bitonicSort(int lo, int n, boolean dir)
{
if (n>1)
{
int m=n/2;
bitonicSort(lo, m, ASCENDING);
bitonicSort(lo+m, m, DESCENDING);
bitonicMerge(lo, n, dir);
}
}
private void bitonicMerge(int lo, int n, boolean dir)
{
if (n>1)
{
int m=n/2;
for (int i=lo; i<lo+m; i++)
compare(i, i+m, dir);
bitonicMerge(lo, m, dir);
bitonicMerge(lo+m, m, dir);
}
}
private void compare(int i, int j, boolean dir)
{
if (dir==(a[i]>a[j]))
exchange(i, j);
}
private void exchange(int i, int j)
{
int t=a[i];
a[i]=a[j];
a[j]=t;
}
} // end class BitonicSorter
Zusammenfassung
Mit Θ(n log(n)2) Vergleichern ist das Verfahren Bitonic Sort nicht optimal – die untere Schranke für Sortierverfahren, die auf Vergleichen beruhen, liegt bei Ω(n log(n)) und wird z.B. von Heapsort auch erreicht. Dennoch ist Bitonic Sort insbesondere für Hardware- und Parallelrechner-Realisierungen interessant, da die Reihenfolge der Vergleiche von vornherein festliegt und nicht von den Daten abhängig ist.
Das Verfahren lässt sich auch für beliebiges n, das keine Zweierpotenz ist, anpassen (Bitonic Sort für beliebiges n).
Literatur
[AKS 83] M. Ajtai, J. Komlos, E. Szemeredi: An
[Bat 68] K.E. Batcher: Sorting Networks and their Applications. Proc. AFIPS Spring Joint Comput. Conf., Vol. 32, 307-314 (1968)
[CLRS 01] T.H. Cormen, C.E. Leiserson, R.L. Rivest, C. Stein: Introduction to Algorithms. 2. Auflage, The MIT Press (2001)
[Knu 73] D.E. Knuth: The Art of Computer Programming, Vol. 3 - Sorting and Searching. Addison-Wesley (1973)
[Lan 12] H.W. Lang: Algorithmen in Java. 3. Auflage, Oldenbourg (2012)
Bitonic Sort und andere Sortiernetze, wie etwa Odd-even Mergesort, sowie die Sortierverfahren Quicksort, Heapsort, Mergesort und Shellsort, finden Sie auch in meinem Buch über Algorithmen.
Weitere
Themen des Buches: parallele Sortieralgorithmen, Textsuche, Graphenalgorithmen, algorithmische Geometrie, Arithmetik, Codierung, Kryptografie, NP-Vollständigkeit, formale Verifikation.
1) von engl. bitonic = zweifach monotonic
Weiter mit: [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 02.02.1997 Updated: 05.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden