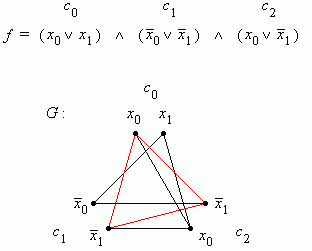NP-Vollständigkeit
Deterministische polynomielle Algorithmen sind bisher für keines der angegebenen Probleme gefunden worden, und es ist fraglich, ob dies jemals geschehen wird. Diese Probleme sind nämlich NP-vollständig; damit gehören sie zu den schwersten Problemen in NP.
Definition: Ein Problem p heißt NP-schwer, wenn sich jedes Problem r, das in NP liegt, in deterministisch polynomieller Zeit auf p reduzieren lässt.
Ein Problem p heißt NP-vollständig, wenn es NP-schwer ist und selbst in NP liegt.
Ein NP-schweres Problem ist also mindestens so schwer wie das schwerste Problem in NP. Ein NP-vollständiges Problem ist NP-schwer und liegt selbst in NP; damit gehört es selbst zu den schwersten Problemen in NP.
Wenn es gelingt, auch nur für ein einziges NP-vollständiges Problem p einen deterministischen polynomiellen Algorithmus zu finden, so lassen sich alle Probleme in NP in deterministisch polynomieller Zeit lösen. Denn alle Probleme in NP lassen sich dann ja in deterministisch polynomieller Zeit auf das Problem p reduzieren und sind damit selbst in deterministisch polynomieller Zeit lösbar. Dann wäre also die Menge NP gleich der Menge P. Vieles spricht jedoch dafür, dass dies nicht gilt.
Um zu zeigen, dass ein Problem q, das in NP liegt, NP-vollständig ist, genügt es, ein anderes NP-vollständiges Problem p in polynomieller Zeit auf q zu reduzieren. Denn dass p NP-vollständig ist, bedeutet ja, dass sich alle Probleme in NP in polynomieller Zeit auf p reduzieren lassen. Indem p nun in polynomieller Zeit weiter auf q reduziert wird, lassen sich somit alle Probleme in NP in polynomieller Zeit auf q reduzieren, und somit ist q ebenfalls NP-vollständig (Bild 1).
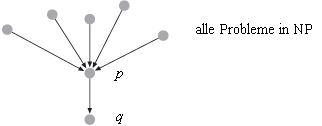
Bild 1: Reduktion eines NP-vollständigen Problems p auf ein Problem q
Als Beispiel für einen solches Vorgehen soll im Folgenden das Erfüllbarkeitsproblem (SAT) in polynomieller Zeit auf das Cliquen-Problem reduziert werden [Koz 92]. Wir wissen, dass das Erfüllbarkeitsproblem NP-vollständig ist, und wir zeigen dadurch, dass das Cliquen-Problem ebenfalls NP-vollständig ist. Wir transformieren also einen beliebigen gegebenen Fall des Erfüllbarkeitsproblems in polynomieller Zeit in einen Fall des Cliquen-Problems, in der Weise, dass die Lösung des Cliquen-Problems (ja oder nein) gleich der Lösung des Erfüllbarkeitsproblems ist.
Gegeben sei ein Fall des Erfüllbarkeitsproblems, also eine boolesche Formel f in konjunktiver Form. Die Formel besteht aus k Oder-Termen c0, ..., ck-1, die durch Und verknüpft sind. Die Oder-Terme enthalten Variablen xi, die auch in negierter Form xi vorkommen können.
Die Formel wird in folgender Weise in einen ungerichteten Graphen G transformiert. Jedes Vorkommen einer Variablen in der Formel f ist ein Knoten des Graphen. Je zwei Knoten sind durch eine Kante verbunden, außer wenn die entsprechenden Vorkommen der Variablen
- im gleichen Oder-Term liegen oder
- zueinander negiert sind.
Die Formel f ist genau dann erfüllbar, wenn der Graph G eine k-Clique enthält. Die Formel f wird erfüllt, wenn die Vorkommen der Variablen, die den Knoten der Clique entsprechen, mit dem Wahrheitswert true belegt werden. Diese Belegung ist widerspruchsfrei, denn zueinander negierte Variablen sind nie durch eine Kante verbunden, und in jedem Oder-Term kommt einmal der Wert true vor.
Beispiel: Die Formel sei
f = (x0 ∨ x1) ∧ (x0 ∨ x1) ∧ (x0 ∨ x1)
Sie besteht aus den drei Oder-Termen c0, c1, c2, d.h. es ist k = 3. Der entsprechend konstruierte Graph ist in Bild 2 dargestellt. Er enthält die 3-Clique mit den Knoten x0 in c0, x1 in c1 und x1 in c2. Mit x0 = true und x1 = false ist die Formel somit erfüllt.
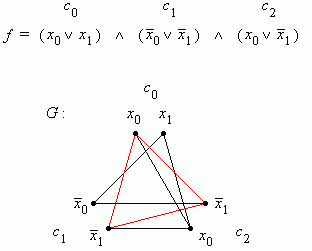
Bild 2: Aus der booleschen Formel f konstruierter Graph G mit 3-Clique
In ähnlicher Weise, durch polynomielle Reduktion eines bekannten NP-vollständigen Problems, sind mittlerweile Tausende von Problemen als NP-vollständig klassifiziert worden [GJ 79]. Das Erfüllbarkeitsproblem ist das Ur-Problem, dessen NP-Vollständigkeit auf andere Weise bewiesen worden ist.
Sucht man einen Lösungsalgorithmus für ein Problem, so prüft man zunächst, ob das Problem in NP liegt. Dann besteht eine gewisse Chance, dass es einen effizienten, also deterministisch polynomiellen Algorithmus zur Lösung des Problems gibt. Findet man jedoch keinen solchen, so versucht man, eines der bekannten NP-vollständigen Probleme auf das Problem zu reduzieren, um zu zeigen, dass es NP-vollständig ist und es somit wahrscheinlich keinen effizienten Algorithmus zu seiner Lösung gibt. Dann bleiben nur noch Approximationsverfahren, die eine gewisse Annäherung an die Lösung liefern (die Faktor-2-Annäherung für das metrische TSP ist ein Beispiel) oder probabilistische Verfahren, die mit einer gewissen Wahrscheinlichkeit die korrekte Lösung liefern (wie etwa der Primzahltest) oder heuristische Verfahren, die mit einer hohen Wahrscheinlichkeit eine gute Annäherung an die Lösung liefern (z.B. das Verfahren Simulated Annealing).
Aufgabe 1: Das Problem des Hamiltonschen Kreises (HC) ist NP-vollständig. Reduzieren Sie HC polynomiell auf das Travelling Salesman Problem (TSP) und zeigen Sie so, dass TSP ebenfalls NP-vollständig ist.
Hinweis: Benutzen Sie die Formulierung von TSP als Entscheidungsproblem. Geben Sie eine Transformation an, die einen beliebigen Fall von HC in einen Fall von TSP umwandelt, derart dass deren Lösungen (ja oder nein) gleich sind. Welche Zeitkomplexität hat die Transformation?
[GJ 79] M.R. Garey, D.S. Johnson: Computers and Intractability. W.H. Freeman (1979)
[Koz 92] D.C. Kozen: The Design and Analysis of Algorithms. Springer (1992)
Weiter mit:
[up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 25.05.2006 Updated: 10.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden