Sortiernetze
Odd-even Mergesort
Das Sortierverfahren Odd-even Mergesort geht auf K.E. Batcher [Bat 68] zurück. Es basiert auf einem Merge-Verfahren, mit dem zwei sortierte Hälften einer Folge zu einer insgesamt sortierten Folge verschmolzen werden (engl.: to merge – verschmelzen).
Im Gegensatz zu Mergesort ist dieses Verfahren nicht datenabhängig, d.h. es werden unabhängig von den Daten stets dieselben Vergleiche durchgeführt. Odd-even Mergesort lässt sich daher als Sortiernetz implementieren.
Merge-Verfahren
Es folgt zunächst das Merge-Verfahren, das eine Folge, deren beide Hälften sortiert sind, zu einer sortierten Folge verschmilzt.
Algorithmus oddevenMerge(n)
Eingabe:
Folge a0, ..., an-1 der Länge n > 1, deren beide Hälften a0, ..., an/2-1 und an/2, ..., an-1 sortiert sind (n Zweierpotenz)
Ausgabe:
Die sortierte Folge
Methode:
- wenn n > 2 dann
- wende oddevenMerge(n/2) rekursiv auf die gerade Teilfolge a0, a2, ..., an-2 und auf die ungerade Teilfolge a1, a3, ..., an-1 an
- Vergleich [i:i+1] für alle i ∈ {1, 3, 5, 7, ..., n-3}
- sonst
- Vergleich [0:1]
Korrektheit
Die Korrektheit des Merge-Verfahrens lässt sich per Induktion und mit Hilfe des 0-1-Prinzips zeigen.
Ist n = 21, so wird mit dem Vergleich [0:1] die Folge sortiert. Sei nun n = 2k, k > 1 und für alle kleineren k sei das Verfahren korrekt (Induktionsvoraussetzung).
Die 0-1-Folge a = a0, ..., an-1 wird gedanklich zeilenweise in ein zweispaltiges Feld eingetragen. Die entsprechende Zuordnung der Indexpositionen ist in Bild 1a gezeigt, hier für n = 16. In Bild 1b ist die dadurch entstehende Situation dargestellt. Jede der beiden sortierten Hälften der 0-1-Folge beginnt mit einer gewissen Anzahl von Nullen (weiß) und endet mit einer gewissen Anzahl von Einsen (grau).
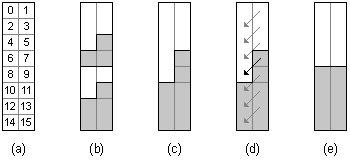
Bild 1: Situationen während der Ausführung von oddevenMerge
In der linken Spalte befindet sich die gerade Teilfolge, d.h. alle ai mit i gerade, also a0, a2, a4 usw.; in der rechten Spalte die ungerade Teilfolge, d.h. alle ai mit i ungerade, also a1, a3, a5 usw. Wie die ursprüngliche Folge bestehen auch die gerade und die ungerade Teilfolge jeweils aus zwei sortierten Hälften.
Nach Induktionsvoraussetzung werden die linke und rechte Spalte durch rekursive Anwendung von oddevenMerge(n/2) in Schritt 1 des Algorithmus sortiert. Die rechte Spalte kann maximal zwei Einsen mehr enthalten als die linke (Bild 1c).
Durch Anwendung der Vergleiche von Schritt 2 des Algorithmus (Bild 1d) wird in jedem Fall das Feld sortiert (Bild 1e).
Analyse
Mit T(n) sei die Anzahl der von oddevenMerge(n) durchgeführten Vergleiche bezeichnet. Dann gilt für n > 2
T(n) = 2·T(n/2) + n/2-1
Mit T(2) = 1 ergibt sich
T(n) = n/2 · (log(n)-1) + 1 ∈ O(n·log(n))
Sortierverfahren
Aus dem Merge-Verfahren lässt sich durch rekursive Anwendung das Sortierverfahren Odd-even Mergesort erzeugen.
Algorithmus oddevenMergesort(n)
Eingabe:
Folge a0, ..., an-1 (n Zweierpotenz)
Ausgabe:
Die sortierte Folge
Methode:
- wenn n > 1 dann
- oddevenMergesort(n/2) rekursiv auf die beiden Hälften a0, ..., an/2-1 und an/2, ..., an-1 der Folge anwenden
- oddevenMerge(n)
Die Anzahl der Vergleicher von Odd-even Mergesort liegt in O(n log(n)2).
Bild 2 zeigt das Odd-even-Mergesort-Sortiernetz für n = 8.
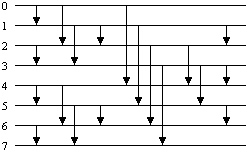
Bild 2: Odd-even Mergesort für n = 8
Programm
Es folgt eine Implementation von Odd-even Mergesort in Java. Das Verfahren ist in der Klasse OddEvenMergeSorter gekapselt. Die Methode sort übergibt das zu sortierende Array an das Array a und ruft die Funktion oddEvenMergeSort auf.
Die Funktion oddEvenMergeSort sortiert zunächst rekursiv die beiden Hälften der Folge. Danach verschmilzt sie die beiden Hälften durch Aufruf von oddEvenMerge.
Die Funktion oddEvenMerge verschmilzt eine Folge, deren beide Hälften sortiert sind. Dies geschieht rekursiv durch Anwendung von oddEvenMerge auf die gerade und die ungerade Teilfolge und anschließendes Vergleichen von benachbarten Elementen. Welche Elemente benachbart sind, wird durch einen Parameter r angegeben: In der ursprünglichen Folge sind Elemente mit dem Abstand r = 1 benachbart; in der geraden Teilfolge sind Elemente mit dem Abstand r = 2 benachbart; in der geraden Teilfolge der geraden Teilfolge sind Elemente mit dem Abstand r = 4 benachbart usw.
Mit den Anweisungen
s.sort(b);
wird ein Objekt vom Typ OddEvenMergeSorter erzeugt und anschließend die Methode sort aufgerufen, um ein Array b zu sortieren. Die Länge n des Arrays muss eine Zweierpotenz sein.
{
private int[] a;
public void sort(int[] a_)
{
a=a_;
oddEvenMergeSort(0, a.length);
}
// sortiert ein Teilstück der Länge n beginnend an Position lo
private void oddEvenMergeSort(int lo, int n)
{
if (n>1)
{
int m=n/2;
oddEvenMergeSort(lo, m);
oddEvenMergeSort(lo+m, m);
oddEvenMerge(lo, n, 1);
}
}
// verschmilzt ein Teilstück der Länge n, das an Position lo beginnt
// r ist der Abstand der zu vergleichenden Elemente
private void oddEvenMerge(int lo, int n, int r)
{
int m=r*2;
if (m<n)
{
oddEvenMerge(lo, n, m); // gerade Teilfolge
oddEvenMerge(lo+r, n, m); // ungerade Teilfolge
for (int i=lo+r; i+r<lo+n; i+=m)
compare(i, i+r);
}
else
compare(lo, lo+r);
}
private void compare(int i, int j)
{
if (a[i]>a[j])
exchange(i, j);
}
private void exchange(int i, int j)
{
int t=a[i];
a[i]=a[j];
a[j]=t;
}
} // end class OddEvenMergeSorter
Zusammenfassung
Dieselbe asymptotische Komplexität wie Odd-even Mergesort haben auch die Sortiernetze Bitonic Sort und Shellsort. Die Anzahl der Vergleicher von Bitonic Sort nähert sich mit wachsendem n an die Anzahl der Vergleicher von Odd-even Mergesort an. Die Anzahl der Vergleicher von Shellsort ist stets um etwa 33% höher als die von Odd-even Mergesort.
Die folgende Tabelle gibt eine Übersicht über die Anzahl der Vergleicher für n = 4, 16, 64, 256 und 1024.
| n | Odd-even Mergesort | Bitonic Sort | Shellsort |
|---|---|---|---|
| 4 | 5 | 6 | 6 |
| 16 | 63 | 80 | 83 |
| 64 | 543 | 672 | 724 |
| 256 | 3839 | 4608 | 5106 |
| 1024 | 24063 | 28160 | 31915 |
Aufgabe 1: Entwickeln Sie die genaue Formel für T(n), die Anzahl der Vergleicher von Odd-even Mergesort. Prüfen Sie die Formel, indem Sie die Ergebnisse mit den Einträgen in oben stehender Tabelle vergleichen.
Literatur
[Bat 68] K.E. Batcher: Sorting Networks and their Applications. Proc. AFIPS Spring Joint Comput. Conf., Vol. 32, 307-314 (1968)
[Sed 03] R. Sedgewick: Algorithms in Java, Parts 1-4. 3. Auflage, Addison-Wesley (2003)
[Lan 12] H.W. Lang: Algorithmen in Java. 3. Auflage, Oldenbourg (2012)
Odd-even Mergesort und andere Sortiernetze, wie etwa Bitonic Sort, sowie die Sortierverfahren Quicksort, Heapsort, Mergesort und Shellsort, finden Sie auch in meinem Buch über Algorithmen.
Weitere Themen des Buches: parallele Sortieralgorithmen, Textsuche, Graphenalgorithmen, algorithmische Geometrie, Arithmetik, Codierung, Kryptografie, NP-Vollständigkeit, formale Verifikation.
Themen des Buches: parallele Sortieralgorithmen, Textsuche, Graphenalgorithmen, algorithmische Geometrie, Arithmetik, Codierung, Kryptografie, NP-Vollständigkeit, formale Verifikation.
Weiter mit: [Bitonic Sort] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 30.03.2001 Updated: 07.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden
