Arithmetik
Bitserielle Arithmetik
Normalerweise arbeiten Arithmetikschaltungen bitparallel, wie etwa der Carry-Lookahead-Addierer oder der Carry-Save-Addierer. In manchen Situationen jedoch, etwa im Bereich hochintegrierter Parallelprozessoren, wird bitseriell gearbeitet. Dies liegt daran, dass die Prozessoren nur über eine einzige, bitserielle Leitung miteinander verbunden sind. Wenn die Kommunikation bitseriell ist, kann auch die Verarbeitung bitseriell durchgeführt werden. Bitserielle Arithmetikschaltungen sind sehr viel kleiner als bitparallele Schaltungen.
Bitserielle Addition
Als bitserieller Addierer eignet sich der Ripple-Carry-Addierer sehr gut. Bild 1 zeigt eine solche Schaltung mit einem Volladdierer (engl.: full adder - FA) im Mittelpunkt. Die Operanden a = a0, ..., an-1 und b = b0, ..., bn-1 werden bitseriell eingegeben, die Summenbits werden bitseriell ausgegeben. Das jeweils entstehende Übertragsbit ci wird in einem Verzögerungselement zwischengespeichert und im nächsten Takt wieder mit eingegeben.
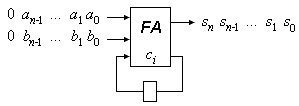
Bild 1: Bitserieller Ripple-Carry-Addierer
Bitserielle Multiplikation
Im Folgenden werden zwei bitserielle Multiplizierer vorgestellt und formal verifiziert. Der erste Multiplizierer wurde im Prozessor des Parallelrechners Systola-1024 verwendet. Der zweite Multiplizierer geht auf Chen und Willoner zurück.
Grundlage für beide Multiplizierer ist das Standard-Multiplikationsschema für zwei n-Bit-Operanden a und b. Je nach dem, in welcher Reihenfolge die einzelnen Bit-Produkte aibj zusammengefasst werden, ergeben sich unterschiedliche Multiplikationsalgorithmen. Die Berechnungen des Multiplikationsalgorithmus werden vom Indexraum {(i,j)} in den Raum {(t,p)} aus Zeit und Prozessorelementen transformiert. Durch unterschiedliche Transformationen sind wiederum unterschiedliche Multipliziererschaltungen möglich.
Weiter mit: [Bitserieller Multiplizierer (1)] [Bitserieller Multiplizierer (2)] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 22.04.2003 Updated: 08.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden