Arithmetik

Wir haben gesehen, dass eine n-Bit-Addition mit einem Ripple-Carry-Addierer Zeit Θ(n) und mit einem Carry-Lookahead-Addierer Zeit Θ(log (n)) benötigt.

Tatsächlich ist es möglich, eine n-Bit-Addition sogar in konstanter Zeit auszuführen. Bei der Carry-Save-Addition werden allerdings nicht zwei Summanden zu einem Ergebnis zusammen­gezählt, sondern drei Summanden zu zwei Ergebnissen. Diese beiden Ergebnisse sind die bei der Addition gebildeten Summenbits und Übertrags­bits.

Das folgende Bild zeigt, wie drei Bits stellen­richtig zu einem Summenbit und einem Übertragsbit zusammen­gezählt werden; ferner eine entsprechende Addition dreier 3-Bit-Zahlen. Das Bit c₀ ist immer 0.

Die Darstellung einer Binärzahl als Paar (s, c) kann als eine Art redundanter Zahlen­darstellung angesehen werden. Nach einer Carry-Save-Addition liegt das Ergebnis in dieser Form vor. Der Carry-Save-Addierer kann auch für die Addition einer normal dar­gestellten und einer redundant dar­gestellten Zahl verwendet werden. Bild 1 zeigt die Addition a + (s, c) = (s', c') mit einem n-Bit-Carry-Save-Addierer.

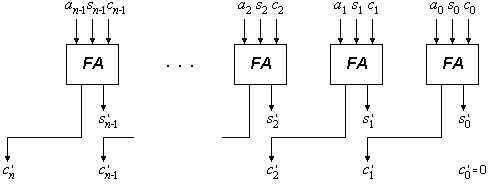
Bild 1: Carry-Save-Addition a + (s, c) = (s', c')

Die Rück­konvertierung von der redundanten Darstellung (s, c) in die normale Binär­darstellung geschieht, indem s und c mit einem Carry-Lookahead-Addierer addiert werden. Dies dauert dann allerdings wieder Zeit Θ(log (n)).

Der Zeitvorteil der Carry-Save-Addition macht sich erst dann bemerkbar, wenn mehrere Zahlen summiert werden sollen. Dann werden alle Additionen als Carry-Save-Additionen ausgeführt und nur die letzte abschließende Konvertierung als Carry-Lookahead-Addition.

Typischer­weise sind bei einer Multi­plikation viele Additionen erforderlich; hier ist es sinnvoll, den Carry-Save-Addierer zu verwenden.

Literatur

[Lan 12]   H.W. Lang: Algorithmen in Java. 3. Auflage, Oldenbourg (2012)

Den Carry-Save-Addierer finden Sie auch in meinem Buch über Algorithmen.
Weitere Themen des Buches: Sortieren, Textsuche, Graphenalgorithmen, algorithmische Geometrie, Codierung, Kryptografie, parallele Sortieralgorithmen.

[Weitere Informationen]