Arithmetik
Ripple-Carry-Addierer
Gegeben sind zwei n-Bit-Zahlen a und b. Die Summe s = a + b wird nach folgendem Schema berechnet, wobei die ci die entstehenden Übertragsbits der jeweils vorherigen Stellen sind (Bild 1):
| an-1 | ... | a1 | a0 | |||||||
| ⊕ | bn-1 | ... | b1 | b0 | ||||||
| ⊕ | cn | cn-1 | ... | c1 | c0 | |||||
| = | sn | sn-1 | ... | s1 | s0 | |||||
Bild 1: Additionsschema
Die Operation ⊕ ist das logische Exklusiv-Oder (Xor). Im Folgenden werden ferner das Zeichen · für das logische Und sowie das Zeichen + für das logische Oder verwendet.
Bei der Addition ist c0 = 0; bei der Subtraktion werden die bi invertiert und es ist c0 = 1.
Die Summenbits si können im Prinzip alle parallel berechnet werden, allerdings nur, wenn die Übertragsbits ci bekannt sind:
si = ai ⊕ bi ⊕ ci (i = 0, ..., n-1).
Die Übertragsbits dagegen hängen vom jeweils vorhergehenden Übertragsbit ab:
ci+1 = ai·bi + ai·ci + bi·ci (i = 0, ..., n-1).
Die Schwierigkeit liegt also in der Berechnung der Übertragsbits. Jedes Übertragsbit ci hängt indirekt von allen aj und bj mit j < i ab. Am schwierigsten zu berechnen ist offenbar das Übertragsbit cn, da es insgesamt von allen Stellen der Zahlen a und b abhängt.
Die normale Schulmethode berechnet die Übertragsbits nacheinander von rechts nach links. Dabei kann es vorkommen, dass ein Übertrag von ganz rechts bis nach ganz links durchklappert. Dies ist z.B. bei der Addition von 00...01 und 11...11 der Fall. Daher benötigt das Verfahren, obwohl die Operandenbits parallel addiert werden, im schlechtesten Fall Θ(n) Zeit. Von dem Durchklappern der Übertragsbits leitet sich der Name des Verfahrens ab: Ripple-Carry-Addition.
Bild 2 zeigt einen aus n Volladdierern (engl.: full adder – FA) aufgebauten n-Bit-Ripple-Carry-Addierer. Ein Volladdierer ist ein Schaltnetz, das die oben angegebenen Funktionen für si und ci+1 realisiert.
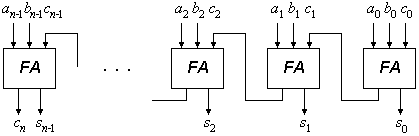
Bild 2: Ripple-Carry-Addierer
Weiter mit: [Carry-Lookahead-Addierer] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 17.04.2002 Updated: 08.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden