Arithmetik
Bitserieller Multiplizierer (1)
Der hier angegebene bitserielle Multiplizierer [SSLH 03] wurde in einer 16-Bit-Version im Prozessor der Systola-1024, einem hochintegrierten Parallelrechner mit 1024 Prozessoren, eingesetzt. Die formale Verifikation der Multipliziererschaltung basiert auf der Methode von Moldovan und Fortes [MF 86].
Multiplikationsschema
Bild 1 zeigt das Standardschema für die Multiplikation zweier n-Bit-Zahlen an-1, ..., a0 und bn-1, ..., b0, hier für n = 3. Die angegebenen Bit-Produkte müssen gebildet werden und stellenrichtig addiert werden.
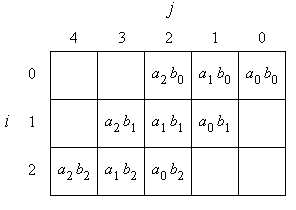
Bild 1: Standardschema für die Multiplikation
Im folgenden Algorithmus wird bei der Addition der Bit-Produkte an jeder Position (i, j) als Zwischenergebnis ein Summenbit si,j und ein Übertragsbit ci,j erzeugt. Diese Zwischenergebnisse und ebenso die Eingabevariablen werden an benachbarte Positionen weitergegeben und dort weiterverarbeitet.
Datenabhängigkeiten
Bild 2 zeigt, wie die Zwischenergebnisse und Eingabevariablen weitergegeben werden. Beispielsweise wird das Summenbit s, das als Zwischenergebnis an Position (i, j) gebildet worden ist, als nächstes an Position (i+1, j) benötigt. Die Eingabevariable a wird von Position (i, j) an Position (i+1, j+1) weitergegeben.
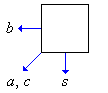
Bild 2: Weitergeben der Eingabevariablen und Zwischenergebnisse
Die Differenz zwischen der Position, an der eine Variable benötigt wird und der Position, an der sie erzeugt wird, ist der Datenabhängigkeitsvektor dieser Variable. Zusammen bilden die Datenabhängigkeitsvektoren aller Variablen die Datenabhängigkeitsmatrix D. Die Datenabhängigkeitsmatrix des obigen Multiplikationsschemas ist
| a | b | s | c | |||||||
| D = | i | 1 | 0 | 1 | 1 | |||||
| j | 1 | 1 | 0 | 1 |
Multiplikationsalgorithmus
Der Multiplikationsalgorithmus ist durch folgende Rekursionsgleichungen gegeben. Hierbei sind die booleschen Funktionen S wie folgt definiert:
Die Funktion Sk hat den Wert 1, wenn genau k ihrer Argumente gleich 1 sind, und sonst 0. Sk,m ist dasselbe wie Sk ∨ Sm. Durch S1,3 und S2,3 werden also das Summenbit und das Übertragsbit berechnet.
Rekursionsgleichungen
| ai+1,j+1 | = | ai,j | ||
| bi,j+1 | = | bi,j | ||
| si+1,j | = | S1,3 (ai,j·bi,j , si,j , ci,j) | ||
| ci+1,j+1 | = | S2,3 (ai,j·bi,j , si,j , ci,j) |
Anfangswerte für die Rekursion sind:
| a0,j | = | aj | ||||
| bi,i | = | bi |
für alle i, j ∈ {0, ..., n-1}. Alle sonstigen Anfangswerte sind 0.
Die Rekursionen werden für alle Indexpositionen (i,j) berechnet, die nötig sind, um das Ergebnis der Multiplikation zu erzeugen. Anders als beim Standardschema der Multiplikation werden die Ergebnisbits nicht "unterm Strich" abgelesen, sondern diagonal. Die Ergebnisbits sind s2n,2n-1, ..., s1,0.
Transformation
Um aus dem Algorithmus eine Schaltung zu erhalten, wird der Indexraum {(i, j)} des Algorithmus in den Indexraum {(t, p)} aus Zeit und Prozessorelementen transformiert. Dies geschieht nach der Methode von Moldovan und Fortes [MF 86]. Die lineare Transformation
| i | j | |||||
| T = | t | 1 | 0 | |||
| p | -1 | 1 |
bildet jede Indexposition (i, j) auf eine entsprechende Indexposition (t, p), bestehend aus Zeit und Prozessorelement, ab. Dabei werden die Indexpositionen als Spaltenvektoren aufgefasst. Beispielsweise ist
T·(1,1)T = (1,0)T,
d.h. die Berechnung an Indexposition (i, j) = (1,1) des Multiplikationsalgorithmus wird zum Zeitpunkt t = 1 in Prozessor p = 0 ausgeführt. Bild 3 zeigt den transformierten Indexraum {(t, p)}.
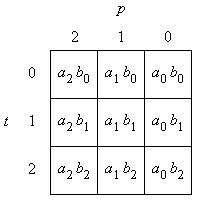
Bild 3: Transformierter Indexraum
Das erste Bit des Multiplikationsergebnisses ist s1,0; es erscheint zum Zeitpunkt t = 1 am Eingang von Prozessorelement p = -1 (d.h. am Ausgang von Prozessorelement p = 0), denn es ist
T · (1, 0)T = (1, -1)T.
Das letzte Ergebnisbit erscheint zum Zeitpunkt t = 2n am Eingang von Prozessorelement p = -1, denn es ist
T · (2n, 2n-1)T = (2n, -1)T.
Die mit der linearen Transformation T transformierte Datenabhängigkeitsmatrix gibt an, in welcher Weise die Variablen im transformierten Indexraum und damit in der Schaltung weitergegeben werden.
| a | b | s | c | |||||||
| TD = | t | 1 | 0 | 1 | 1 | |||||
| p | 0 | 1 | -1 | 0 |
So wird beispielsweise s in jedem Takt zum vorherigen Prozessorelement weitergegeben, c wird in jedem Takt im selben Prozessorelement gespeichert, a wird ebenfalls in jedem Takt im selben Prozessorelement gehalten, b wird in Null Takten jeweils um ein Prozessorelement weitergegeben, d.h. es wird gleichzeitig an alle Prozessorelemente gegeben.
Die Bits des Operanden a müssen somit offenbar parallel an den Prozessorelementen anliegen. Es ist jedoch möglich, den Operanden a vor Beginn der eigentlichen Multiplikation bitseriell einzugeben und mit Hilfe eines Steuersignals in den Prozessorelementen zu speichern.
Bitserieller Multiplizierer
Das folgende Bild 4 zeigt die entsprechende Multipliziererschaltung, hier für eine Operandenlänge von n = 3. Jedes der n Prozessorelemente besteht aus einem AND-Gatter zur Bildung des Bit-Produktes, einem Volladdierer (full adder), sowie zwei Verzögerungselementen.
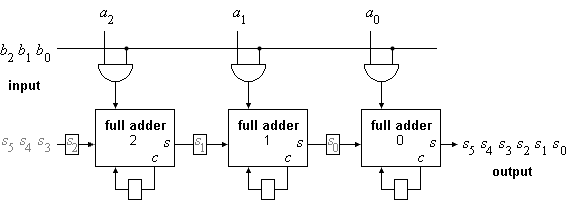
Bild 4: Bit-serieller Multiplizierer für Operanden der Länge n = 3
Es ist möglich, zusätzlich einen Operanden s einzugeben und damit s = s + a·b zu berechnen. Die ersten n Bits müssen vor Beginn der eigentlichen Multiplikation in den Multiplizierer geladen werden.
Der Multiplizierer benötigt n Takte zum Laden des Operanden a und der ersten n Bits von s, anschließend dann noch weitere 2n Takte zur Ausgabe des Ergebnisses, also insgesamt 3n Takte.
Zusammenfassung
Der hier vorgestellte bitserielle Multiplizierer für n-Bit-Operanden besteht aus n Prozessorelementen, die im Wesentlichen jeweils ein AND-Gatter, einen Volladdierer sowie Verzögerungselemente enthalten. Alle Operanden werden bitseriell eingegeben, das Ergebnis wird bitseriell ausgegeben. Eine Multiplikation dauert 3n Takte. Die Korrektheit der Schaltung ergibt sich unmittelbar durch Transformation des Standard-Multiplikationsschemas.
Literatur
[SSLH 03] M. Schimmler, B. Schmidt, H.W. Lang, S. Heithecker: An Area-Efficient Bit-Serial Integer Multiplier. In: H.R. Arabnia, L.T. Yang (Eds.): Proceedings of the International Conference on VLSI, CSREA Press (2003)
[MF 86] D.I. Moldovan, J.A.B. Fortes: Partitioning and Mapping Algorithms into Fixed Size Systolic Arrays. IEEE Transactions on Computers C-35, 1, 1-12 (1986)
[Web 1] http://www.inf.fh-flensburg.de/lang/papers/multipli/multipli.htm
Weiter mit: [Bitserieller Multiplizierer (2)] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 08.04.2003 Updated: 08.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden