Arithmetik
Bitserieller Multiplizierer (2)
Dieser bitserielle Multiplizierer basiert auf einem Multiplikationsschema, das von Chen und Willoner [CW 79] angegeben wurde. Die ursprüngliche Implementation wurde unabhängig voneinander von Sips [Sips 82], Gnanasekaran [Gna 83] sowie von Strader und Rhyne [SR 82] verbessert. Diese Implementation wird im Folgenden vorgestellt und mit Hilfe der Methode von Moldovan und Fortes [MF 86] formal verifiziert.
Multiplikationsalgorithmus
Für die Multiplikation zweier n-Bit-Zahlen an-1, ..., a0 und bn-1, ..., b0 müssen die in Bild 1a für n = 4 angegebenen Bit-Produkte gebildet und stellenrichtig addiert werden.
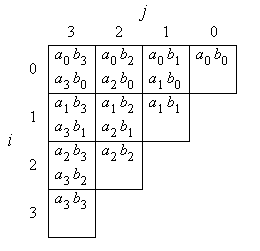
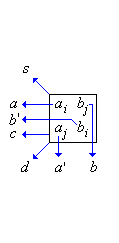
Bild 1: Bit-Produkte bei einer 4-Bit-Multiplikation (a), Weitergabe der Zwischenergebnisse und Eingabebits (b)
Im Multiplikationsalgorithmus werden an jeder Indexposition (i,j) mit i ≤ j die beiden Bit-Produkte aibj und ajbi (bzw. nur das eine Bit-Produkt aibi, falls i = j) berechnet und mit drei weiteren Bits, die als Zwischenergebnisse auftreten, summiert. Da insgesamt fünf Bits addiert werden, ist das Ergebnis eine Zahl zwischen 0 und 5, für deren Darstellung drei Bit erforderlich sind. Diese drei Ergebnisbits sind das Summenbit s, ein Übertragsbit c und ein Übertragsbit zweiter Ordnung d.
Die boolesche Funktion, die diese Ergebnisbits berechnet, wird als (5,3)-Zähler bezeichnet, denn sie zählt, wieviele der 5 Eingabebits gleich 1 sind und stellt das Ergebnis durch 3 Ausgabebits dar.1)
Die Bit-Produkte, die an Position (i,j) berechnet werden, haben einen binären Stellenwert von 2i+j. Das dort berechnete Summenbit s hat ebenfalls einen Stellenwert von 2i+j, das Übertragsbit c hat einen Stellenwert von 2i+j+1, und das Übertragsbit zweiter Ordnung d hat einen Stellenwert von 2i+j+2. Diese Ergebnisbits werden nun an andere Indexpositionen weitergegeben, an denen Berechnungen mit dem jeweils passenden Stellenwert stattfinden. Bild 1b zeigt die Weitergabe der Ergebnisbits sowie der Eingabebits.
Die Eingabebits werden in den zweidimensionalen Indexraum eingebettet, indem
| ai,j | = | ai |
| bi,j | = | bj |
| a'i,j | = | aj |
| b'i,j | = | bi |
für alle i, j ∈ {0, ..., n-1} mit i ≤ j gesetzt wird. Hierbei stehen ai,j und bi,j für die oberen Eingabebits in den Kästchen von Bild 1 und a'i,j und b'i,j für die unteren Eingabebits. So entspricht a0b3 beispielsweise a0,3b0,3, und a3b0 entspricht a'0,3b'0,3.
Der Multiplikationsalgorithmus kann nun durch folgende Rekursionsgleichungen dargestellt werden. Die Funktionen S sind symmetrische boolesche Funktionen, die wie folgt definiert sind:
Die Funktion Sk ist gleich 1, falls genau k ihrer Argumente gleich 1 sind, und sonst 0. Sk,m steht abkürzend für Sk ∨ Sm. Zusammengenommen bilden S1,3,5, S2,3 und S4,5 einen (5,3)-Zähler.
Rekursionsgleichungen
| ai,j+1 | = | ai,j |
| bi+1,j | = | bi,j |
| a'i+1,j | = | a'i,j |
| b'i,j+1 | = | b'i,j |
| si-1,j+1 | = | S1,3,5 (ai,j bi,j , a'i,j b'i,j , si,j , ci,j , di,j) |
| ci,j+1 | = | S2,3 (Argumente wie oben) |
| di+1,j+1 | = | S4,5 (Argumente wie oben) |
Das Ergebnis der Multiplikation sind die Bits rj = s-1,j+1 mit j = 0, ..., 2n-1. Der Indexraum, der in Bild 1 dargestellt ist, muss also so erweitert werden, dass die Summen- und Übertragsbits zu den entsprechenden Indexpositionen mit j ≥ n weitergegeben werden können. Die Eingabebits a'i,j und bi,j sind 0 für j ≥ n, sodass die im erweiterten Indexraum berechneten Bit-Produkte ebenfalls 0 sind.
Transformation des Indexraums
Um aus den Rekursionsgleichungen die Multipliziererschaltung zu gewinnen, wird der Indexraum {(i,j)} in den Indexraum {(t,p)} aus Zeit und Prozessorelementen transformiert [MF 86].
Die lineare Transformation
| i | j | |||||
| T = | t | 0 | 1 | |||
| p | 1 | 0 |
transponiert im Wesentlichen das Schema von Bild 1. Das Ergebnis ist das folgende Schema (Bild 2). Es ist zu sehen, dass beispielsweise a0 b1 und a1 b0 zur Zeit 1 in Prozessorelement 0 berechnet werden.
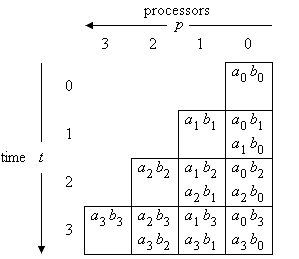
Bild 2: Transformierter Indexraum
Die Anwendung der Transformation auf die Indexpositionen, an denen das Ergebnis der Multiplikation erzeugt wird, ergibt folgendes:
Das Ergebnis der Multiplikation erscheint bei Prozessorelement -1 (d.h. am Ausgang von Prozessorelement 0) zu den Zeitpunkten 1, ..., 2n. Es sind also noch zusätzliche n Takte erforderlich, um die n höher signifikanten Ergebnisbits aus dem Prozessorfeld herauszuschieben.
Die Datenabhängigkeitsmatrix D der Rekursionsgleichungen im Indexraum {(i,j)} ist
| s | c | d | a | b | a' | b' | ||||||||||
| D = | i | -1 | 0 | 1 | 0 | 1 | 1 | 0 | ||||||||
| j | 1 | 1 | 1 | 1 | 0 | 0 | 1 |
Die Datenabhängigkeiten bedeuten, dass z.B. die Variable s, die an Indexposition (i,j) berechnet worden ist, als nächstes an Indexposition (i-1,j+1) gebraucht wird, oder dass z.B. die Variable y von Indexposition (i,j) auch an Indexposition (i,j+1) gebraucht wird.
Die mit der linearen Transformation T transformierte Datenabhängigkeitsmatrix gibt an, in welcher Weise die Variablen im transformierten Indexraum und damit in der Schaltung weitergegeben werden.
| s | c | d | a | b | a' | b' | ||||||||||
| TD = | t | 1 | 1 | 1 | 1 | 0 | 0 | 1 | ||||||||
| p | -1 | 0 | 1 | 0 | 1 | 1 | 0 |
Beispielsweise wird s in jedem Takt an das vorhergehende Prozessorelement weitergegeben, c wird in jedem Takt im selben Prozessorelement gehalten, d wird in jedem Takt zum nächsten Prozessorelement weitergegeben. Die Eingabebits b und a' werden in 0 Takten zum jeweils nächsten Prozessorelement weitergegeben – dies bedeutet, dass sie gleichzeitig an alle Prozessorelemente gesendet werden.
Die Eingabebits a und b' werden in jedem Takt im selben Prozessorelement gehalten. Sie müssen also offenbar bitparallel an den Prozessorelementen anliegen. Zum Zeitpunkt 0 werden aber zunächst nur a0 und b'0 gebraucht, zum Zeitpunkt 1 dann zusätzlich a1 und b'1 usw. Daher werden a und b' ebenfalls bitseriell eingegeben und mit Hilfe eines Steuersignals jeweils zum Zeitpunkt k in Prozessorelement k gespeichert..
Multipliziererschaltung
Bild 3 zeigt den Multiplizierer, hier für eine Operandenlänge von n = 3. Jedes der n Prozessorelemente besteht aus zwei Latches zur Speicherung der Eingabebits a und b', zwei AND-Gattern zur Bildung der Bit-Produkte, einem (5,3)-Zähler und vier Verzögerungselementen.
Im Takt k soll in Prozessor k jeweils nur ein Bit-Produkt ak bk addiert werden (siehe Bild 2). In diesem Fall wird das andere Bit-Produkt durch das Steuersignal auf 0 gesetzt.
Es ist möglich, gleichzeitig noch eine Addition auszuführen, indem ein Operand s in den d-Eingang von Prozessor 0 eingegeben wird (Eingabebits s0 s1 s2 in Bild 3). Der Multiplizierer berechnet dann r = s + a·b.

Bild 3: Multipliziererschaltung für Operanden der Länge n=3
Eine Simulation des Multiplizierers in Form einer Excel-Datei steht unter Serieller Multiplizierer 2.xls zur Verfügung.
Zusammenfassung
Es wurde der bitserielle Multiplizierer von [Sips 82][SR 82][Gna 83] vorgestellt und mit Hilfe des Transformationsverfahrens von [MF 86] formal verifiziert. Das zugrunde liegende Multiplikationsschema stammt von Chen und Willoner [CW 79]. Die ursprünglich dort angegebene Implementation entspricht einer weniger günstigen Transformation T, nämlich
| i | j | |||||
| T = | t | 0 | 1 | |||
| p | 1 | 1 |
Das Ergebnis dieser Transformation ist ein Feld mit 2n Prozessorelementen.
Literatur
[CW 79] I.N. Chen, R. Willoner: An
[Gna 83] R. Gnanasekaran: On a Bit-Serial Input and Bit-Serial Output Multiplier. IEEE Transactions on Computers C-32, 9, 878-880 (1983)
[MF 86] D.I. Moldovan, J.A.B. Fortes: Partitioning and Mapping Algorithms into Fixed Size Systolic Arrays. IEEE Transactions on Computers C-35, 1, 1-12 (1986)
[Sips 82] H.J. Sips: Comments on "An O(n) Parallel Multiplier with Bit-Sequential Input and Output". IEEE Transactions on Computers C-31, 4, 325-327 (1982)
[SR 82] N.R. Strader, V.T. Rhyne: A Canonical Bit-Sequential Multiplier. IEEE Transactions on Computers C-31, 8, 791-795 (1982)
1) Ein Volladdierer ist entsprechend ein (3,2)-Zähler.
Weiter mit: [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 22.04.2003 Updated: 08.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden