Arithmetik
Carry-Lookahead-Addierer
Das Carry-Lookahead-Verfahren ist ein paralleles Verfahren zur Berechnung der Summe von zwei n-Bit-Binärzahlen in Zeit O(log(n)).
Problem
Gegeben sind zwei n-Bit-Zahlen a und b. Die Summe s = a + b wird nach folgendem Schema berechnet, wobei die ci die entstehenden Übertragsbits sind (Bild 1):
| an-1 | ... | a1 | a0 | |||||||
| ⊕ | bn-1 | ... | b1 | b0 | ||||||
| ⊕ | cn | cn-1 | ... | c1 | c0 | |||||
| = | sn | sn-1 | ... | s1 | s0 | |||||
Bild 1: Additionsschema
Bei der Addition ist c0 = 0; bei der Subtraktion werden die bi invertiert und es ist c0 = 1. Die Operation ⊕ ist das logische Exklusiv-Oder (Xor). Im Folgenden werden ferner das Symbol · für das logische Und sowie das Symbol + für das logische Oder verwendet.
Die normale Schulmethode berechnet die Übertragsbits nacheinander von rechts nach links. Dabei kann es vorkommen, dass ein Übertrag von ganz rechts bis nach ganz links durchklappert. Dies ist z.B. bei der Addition von 00...01 und 11...11 der Fall. Daher benötigt das Verfahren im schlechtesten Fall Θ(n) Zeit. Von dem Durchklappern der Übertragsbits leitet sich der Name des Verfahrens ab: Ripple-Carry-Addierer.
Es stellt sich die Frage, ob sich die Addition durch Parallelverarbeitung schneller als in Zeit Θ(n) durchführen lässt. Die Summenbits si können alle parallel berechnet werden, wenn die Übertragsbits ci bekannt sind:
si = ai ⊕ bi ⊕ ci.
Die Schwierigkeit liegt also in der Berechnung der Übertragsbits. Jedes Übertragsbit ci hängt von allen aj und bj mit j < i ab. Am schwierigsten zu berechnen ist offenbar das Übertragsbit cn, da es von allen Stellen der Zahlen a und b abhängt.
Idee
Beim Carry-Lookahead-Verfahren wird die in den Stellen 0, ..., n-1 enthaltene Information, die zum Wert von cn beiträgt, über einen vollständigen binären Baum in O(log(n)) Schritten zusammengefasst. Die benötigte Information ist die folgende:
Entsteht irgendwo innerhalb der Stellen 0, ..., n-1 ein Übertrag ck+1 (dadurch, dass ak · bk = 1 ist) und klappert dieser Übertrag nach links bis an Position n durch (dadurch dass an allen Positionen i mit k < i < n gilt: ai + bi = 1)?1) Dann bedeutet dies, dass die Stellen 0, ..., n-1 einen Übertrag generieren:
g(0, n-1) = 1.
Oder ist c0 = 1 und klappert es bis an Position n durch (dadurch dass an allen Positionen i mit 0 ≤ i < n gilt: ai + bi = 1)? Dann bedeutet dies, dass die Stellen 0, ..., n-1 einen Übertrag propagieren:
p(0, n-1) = 1.
Das folgende Bild 2 zeigt das Additionsschema ohne Summenbits sowie andeutungsweise die beiden eben geschilderten Möglichkeiten:

Bild 2: (a) Additionsschema, (b) Generieren eines Übertrags, (c) Propagieren des Übertrags c0
Durch Verwendung der Funktionen g und p ergibt sich also
cn = g(0, n-1) + c0 · p(0, n-1),
d.h. das Übertragsbit cn ist gleich 1, wenn die Stellen 0, ..., n-1 einen Übertrag generieren oder wenn c0 gleich 1 ist und die Stellen 0, ..., n-1 den Übertrag propagieren.
Diese an sich triviale Tatsache bekommt dadurch ihre Bedeutung, dass sich die Funktionen g und p rekursiv in O(log(n)) Schritten berechnen lassen.
Berechnung der Funktionen g und p
Es gilt für alle i ≤ k < j:
p(i, j) = p(i, k) · p(k+1, j) und
g(i, j) = g(k+1, j) + g(i, k) · p(k+1, j).
Für i = j gilt:
p(i, i) = ai + bi und
g(i, i) = ai · bi.
In Bild 3 ist das Zustandekommen von p(i, j) sowie von g(i, j) schematisch dargestellt. Die Stellen von i bis j propagieren einen Übertrag, wenn zunächst die Stellen von i bis k den Übertrag propagieren und dann die Stellen von k+1 bis j den Übertrag weiterpropagieren (Bild 3 a). Die Stellen von i bis j generieren einen Übertrag, wenn die Stellen von k+1 bis j einen Übertrag generieren (Bild 3 b) oder wenn die Stellen von i bis k einen Übertrag generieren und die Stellen von k+1 bis j den Übertrag propagieren (Bild 3 c).

Bild 3: Berechnung von p(i, j) = p(i, k) · p(k+1, j), g(k+1, j) und g(i, k) · p(k+1, j)
Die Werte g(0, n-1) und p(0, n-1) lassen sich nach dem Divide-and-Conquer-Prinzip effizient berechnen. Das Problem wird in zwei Hälften geteilt und die Teilprobleme parallel nach derselben Methode gelöst. Beispielsweise wird g(0, n-1) wie folgt berechnet (im Folgenden sei der Einfachheit halber vorausgesetzt, dass n eine Zweierpotenz ist):
effizient berechnen. Das Problem wird in zwei Hälften geteilt und die Teilprobleme parallel nach derselben Methode gelöst. Beispielsweise wird g(0, n-1) wie folgt berechnet (im Folgenden sei der Einfachheit halber vorausgesetzt, dass n eine Zweierpotenz ist):
g(0, n-1) = g(n/2, n-1) + g(0, n/2-1) · p(n/2, n-1).
Die Teilprobleme g(n/2, n-1), g(0, n/2-1) und p(n/2, n-1) werden wiederum in kleinere Teilprobleme aufgespalten usw., bis sich schließlich Teilprobleme der Länge 1 ergeben, die direkt aus a und b berechnet werden können. Das folgende Bild 4 zeigt den Datenflussgraphen für n = 8.
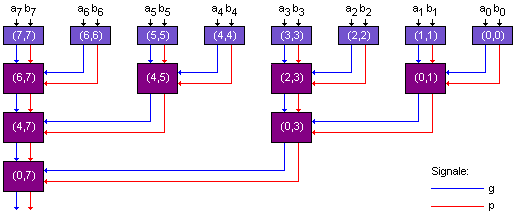
Bild 4: Datenfluss bei der Berechnung von g(0,7) und p(0,7)
Berechnung aller Übertragsbits
Bisher ist lediglich
cn = g(0, n-1) + c0 · p(0, n-1)
berechnet worden. Auf ähnliche Weise lassen sich auch die anderen Übertragsbits berechnen, und zwar in O(log(n)) Schritten unter Verwendung der bereits berechneten g- und p-Werte sowie bereits berechneter Übertragsbits (indem der Baum aus Bild 4 in noch einmal umgekehrter Richtung durchlaufen wird).
Es gilt nämlich für beliebige i, k ∈ {1, ..., n} mit i < k:
ck = g(i, k-1) + ci · p(i, k-1),
d.h. ein Übertragsbit ck ist gleich 1, wenn es von den Stellen i, ..., k-1 generiert wird oder wenn ci gleich 1 ist und es von den Stellen i, ..., k-1 propagiert wird.
Dies wird benutzt, um z.B. c6 mithilfe von c4 zu berechnen:
c6 = g(4, 5) + c4 · p(4, 5).
Bild 5 zeigt die entsprechende Erweiterung von Bild 4 zur Berechnung der Übertragsbits und der Summenbits.
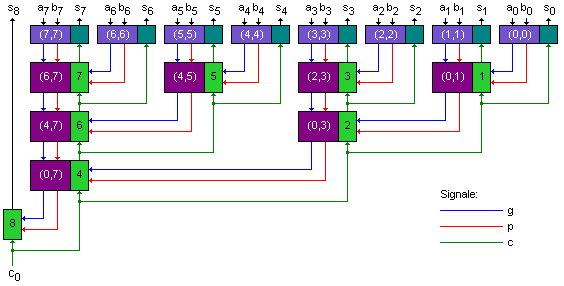
Bild 5: Datenfluss des Carry-Lookahead-Addierers
Schaltbild
Der Datenflussgraph des Carry-Lookahead-Addierers lässt sich direkt in eine Schaltung umsetzen; diese besteht aus folgenden Bausteinen , die farblich wie die entsprechenden Knoten des Datenflussgraphen gekennzeichnet sind (Bild 6). 2)

Bild 6: Bausteine des Carry-Lookahead-Addierers
Analyse
Die Schaltzeiten für die einzelnen Bausteine sind die folgenden:
| blauer Kasten: | 1 | |
| violetter Kasten: | 2 | |
| grüner Kasten: | 2 | |
| türkiser Kasten: | 3 (Xor-Gatter) |
Der violette Baum hat die Tiefe log(n), der grüne Baum ebenfalls log(n). Der längste Datenpfad führt offenbar zu cn-1; er durchläuft den violetten Baum nur bis zur vorletzten Stufe. Damit beträgt die Schaltzeit des Carry-Lookahead-Addierers
T(n) = 1 + 2·(log(n)-1) + 2·log(n) + 3 = 4·log(n) + 2.
Algorithmus
Die folgende Funktion simuliert den Carry-Lookahead-Addierer. Die Funktion addiert zwei n-Bit-Binärzahlen, deren Bits in den Arrays a und b stehen, und liefert die Summe im Array s. Die einzelnen Bits werden mit den Operationen | (Oder), & (Und) sowie ^ (Xor) verknüpft. In diesem Programm braucht n keine Zweierpotenz zu sein.
{
int[] c=new int[n+1];
int[] g=new int[n+1];
int[] p=new int[n+1];
int i, h;
c[0]=0;
// Berechnung der g[i,i] und p[i,i];
// Speicherung an Position i+1
for (i=0; i<n; i++)
{
g[i+1]=a[i] & b[i];
p[i+1]=a[i] | b[i];
}
// Berechnung der übrigen g- und p-Werte;
// nicht mehr benötigte Werte werden überschrieben
// (z.B. g[1,1] durch g[0,1] usw.)
for (h=2; h<=n; h*=2)
for (i=h; i<=n; i+=h)
{
g[i]=g[i] | g[i-h/2] & p[i];
p[i]=p[i] & p[i-h/2];
}
// Berechnung der Übertragsbits
for (h=h/2; h>=1; h/=2)
for (i=h; i<=n; i+=h+h)
c[i]=g[i] | c[i-h] & p[i];
// Berechnung der Summenbits
for (i=0; i<n; i++)
s[i]=a[i] ^ b[i] ^ c[i];
s[n]=c[n];
}
Literatur
[CLRS 01] T.H. Cormen, C.E. Leiserson, R.L. Rivest, C. Stein: Introduction to Algorithms. 2. Auflage, The MIT Press (2001)
[HP 96] J.L. Hennessy, D.A. Patterson: Computer Architecture -- a Quantitative Approach. 2. Auflage, Morgan Kaufmann (1996)
[Lan 12] H.W. Lang: Algorithmen in Java. 3. Auflage, Oldenbourg (2012)
Den Carry-Lookahead-Addierer finden Sie auch in meinem Buch über Algorithmen.
Weitere Themen des Buches: Sortieren, Textsuche, Graphenalgorithmen, algorithmische Geometrie, Codierung, Kryptografie, parallele Sortieralgorithmen.
Themen des Buches: Sortieren, Textsuche, Graphenalgorithmen, algorithmische Geometrie, Codierung, Kryptografie, parallele Sortieralgorithmen.
1) Tatsächlich genügt ai ⊕ bi = 1. Aber + funktioniert auch und ist leichter zu implementieren.
2) Statt der DIN-Schaltsymbole sind die alten Schaltsymbole verwendet worden, da sie den Signalfluss (Eingänge/Ausgänge) besser veranschaulichen.
Weiter mit: [Carry-Save-Addierer] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 31.08.1998 Updated: 08.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden
