Theoretische Informatik
Mächtigkeiten der Mengen aller Wörter bzw. aller Sprachen über einem Alphabet
Ein Alphabet A ist eine nichtleere, endliche Menge von Zeichen. Ein Wort über A ist eine endliche Folge von Zeichen aus A. Die Menge aller Wörter über A wird mit A* bezeichnet. Eine Sprache über A ist eine Teilmenge von A*.
Mächtigkeit der Menge aller Wörter über A
Satz: Sei A ein Alphabet. Es gibt abzählbar unendlich viele Wörter über A, d.h. die Menge A* aller Wörter über A hat die Mächtigkeit abzählbar unendlich:
| A* | = ℵ0
Beweis: Angenommen, die Menge A* wäre endlich. Dann enthält A* ein Wort w maximaler Länge (A* ist nicht leer, denn A* enthält zumindest das leere Wort ε). Sei a ein Zeichen aus dem Alphabet A (das Alphabet A ist nicht leer). Dann ist wa ein Wort über A, d.h. wa ∈ A*, aber andererseits wa ∉ A*, da A* nur Wörter der Länge ≤ |w| enthält und |wa| > |w| gilt. Dies ist ein Widerspruch; also ist die Annahme falsch.
A* enthält also unendlich viele Elemente, selbst dann, wenn das Alphabet A nur aus einem einzigen Zeichen besteht.
Um zu zeigen, dass A* abzählbar unendlich viele Wörter enthält, benötigen wir eine bijektive Abbildung zwischen A* und ℕ. Hierzu definieren wir eine Ordnung auf A; anschließend ordnen wir die Wörter von A* zunächst ihrer Länge nach und dann bei gleicher Länge lexikographisch (wie im Lexikon) unter Zugrundelegung der Ordnung von A. Diese Ordnung auf A* wird als längen-lexikographische Ordnung bezeichnet. Die bijektive Abbildung zwischen A* und ℕ ergibt sich, indem jedes Wort von A* auf die Position abgebildet wird, in der es in der längen-lexikographischen Ordnung auftritt.
Beispiel: Sei A = {a, b, c} das Alphabet. Die Ordnung auf A sei a < b < c. Dann lassen sich die Wörter von A* gemäß der längen-lexikographischen Ordnung wie folgt anordnen und abzählen:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | ... |
| ε | a | b | c | aa | ab | ac | ba | bb | bc | ca | cb | cc | aaa | aab | aac | ... |
Mächtigkeit der Menge aller Sprachen über A
Eine Sprache über einem Alphabet A ist eine beliebige Menge von Wörtern, also eine Teilmenge von A*. Wie viele solche Teilmengen, also wie viele Sprachen gibt es?
Offenbar ist die Menge ℒA aller Sprachen über dem Alphabet A gleich der Menge aller Teilmengen von A*, also der Potenzmenge von A*:
ℒA = 
(A*)
Stets ist es so, dass die Potenzmenge (M) einer beliebigen Menge M eine größere Mächtigkeit hat als M. Die Menge A* aller Wörter über A ist abzählbar unendlich, daher ist die Potenzmenge (A*) überabzählbar unendlich. Wir zeigen dies im Folgenden noch einmal explizit.
Satz: Sei A ein Alphabet. Es gibt überabzählbar unendlich viele Sprachen über A, d.h. die Mächtigkeit der Menge aller Sprachen über A ist überabzählbar unendlich.
Der Satz lässt sich mit dem 2. Cantorschen Diagonalverfahren beweisen (nach G. Cantor
).
Beweis:
Angenommen, die Menge aller Sprachen über A wäre abzählbar. Dann lassen sich die Sprachen als L1, L2, L3, ... abzählen und in folgendes Schema eintragen:
| w1 | w2 | w3 | w4 | w5 | w6 | ... | |
|---|---|---|---|---|---|---|---|
| L1 | 1 | 1 | 1 | 0 | 1 | 1 | ... |
| L2 | 1 | 0 | 1 | 0 | 1 | 0 | ... |
| L3 | 0 | 1 | 1 | 0 | 0 | 1 | ... |
 |  |
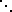Die Spalten des Schemas sind mit den Wörtern von A* überschrieben, beispielsweise in längen-lexikographischer Anordnung. Jede Zeile i enthält die charakteristische Funktion der Sprache Li bezüglich A*, d.h. in der mit wj überschriebenen Spalte steht eine 1, wenn wj ∈ Li gilt und 0 sonst. Beispielsweise enthält L2 die Wörter w1, w3, w5, ...
Wir betrachten nun die Diagonale des Schemas (hellgelbe Felder). Die dort befindlichen Felder enthalten die charakteristische Funktion der Diagonalsprache Ld. Die Sprache Ld enthält hier die Wörter w1, w3, ...
Das Komplement Ld der Diagonalsprache Ld ist nun eine Sprache, die in diesem Schema nicht vorkommen kann. Denn Ld kann keines der Li sein, weil Ld definitionsgemäß in der i-ten Spalte des Schemas genau dann eine 0 hat, wenn Li dort eine 1 hat, und umgekehrt.
Wir hatten angenommen, dass wir alle Sprachen in das Schema eingetragen haben und finden nun eine Sprache, die nicht in dem Schema auftritt. Dies ist ein Widerspruch. Daher kann die Menge aller Sprachen nicht abzählbar sein.
Sprachen mit endlicher Beschreibung
Es gibt also überabzählbar viele, also sehr, sehr viele Sprachen. Die meisten dieser Sprachen allerdings lassen sich gar nicht explizit angeben, weil sie keine endliche Beschreibung besitzen.
Eine endliche Beschreibung einer Sprache ist beispielsweise ein regulärer Ausdruck oder eine Grammatik oder auch eine informelle Beschreibung in Textform. Aber alle diese endlichen Beschreibungen sind endliche Zeichenfolgen, also Wörter, über einem zugrundeliegenden Alphabet.
Es gibt aber nur abzählbar viele Wörter über einem Alphabet. Also gibt es auch nur abzählbar viele endliche Beschreibungen. Also gibt es auch nur abzählbar viele Sprachen, die eine endliche Beschreibung besitzen. Dies sind, gegenüber der überwältigend großen Menge aller Sprachen, die wenigsten.
Weiter mit: [Reguläre Sprachen] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 26.09.2010 Updated: 16.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden