Mathematische Grundlagen
Relation
Eine Relation ist nichts anderes als eine Teilmenge eines kartesischen Produkts.
Definition
Definition: Seien A und B Mengen. Eine Teilmenge R ⊆ A × B heißt (zweistellige) Relation zwischen A und B. Gilt A = B, so heißt R Relation auf A.
Schreibweise: Statt (a, b) ∈ R schreibt man im Allgemeinen a R b; statt des Buchstabens R verwendet man bei Relationen meist spezielle Symbole: = , ≤ , < , ⊆ , ~ , ...
Beispiel: Die folgende Mengen stellen die Kleiner- bzw. die Gleichheitsrelation auf der Menge ℕ dar:
< = { (1,2), (1,3), (2,3), (1,4) ... } ⊆ ℕ × ℕ
= = { (1,1), (2,2), (3,3), (4,4) ... } ⊆ ℕ × ℕ
Eigenschaften von Relationen
Definition: Sei R eine Relation auf einer Menge A. Wenn für alle Elemente a, b, c ∈ A jeweils das Folgende gilt, dann wird die Relation R bezeichnet als
| reflexiv: | (a, a) ∈ R |
| antisymmetrisch: | (a,b) ∈ R ∧ (b, a) ∈ R ⇒ a = b |
| transitiv: | (a, b) ∈ R ∧ (b, c) ∈ R ⇒ (a, c) ∈ R |
| symmetrisch: | (a, b) ∈ R ⇔ (b, a) ∈ R |
| irreflexiv: | (a, a) ∉ R |
| total: | a ≠ b ⇒ (a, b) ∈ R ∨ (b, a) ∈ R |
Beispiel: Sei M die Menge aller Menschen. Die Relation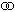 
("ist verheiratet mit") auf M ist symmetrisch (wenn a mit b verheiratet ist, dann ist auch b mit a verheiratet), irreflexiv (niemand ist mit sich selbst verheiratet), aber nicht total (es gibt unverheiratete Menschen).
Die Relation ~ ("hat dieselben Eltern wie") auf M ist reflexiv (jeder hat dieselben Eltern wie er selbst), symmetrisch (wenn a dieselben Eltern hat wie b, dann hat auch b dieselben Eltern wie a) und transitiv (wenn a dieselben Eltern hat wie b und b dieselben Eltern hat wie c, dann hat auch a dieselben Eltern wie c).
Die Relation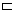 
("ist Vorfahre von") auf M ist antisymmetrisch (wenn a Vorfahre von b ist und b Vorfahre von a ist, dann sind a und b gleich – die Aussage ist wahr, da die ersten beiden Bedingungen nie gleichzeitig eintreten können), transitiv (wenn a Vorfahre von b ist und b Vorfahre von c ist, dann ist a Vorfahre von c) und irreflexiv (niemand ist Vorfahre von sich selbst).
Eine (nichtleere) Relation kann nicht gleichzeitig reflexiv und irreflexiv sein. Aber es gibt Relationen, die weder reflexiv noch irreflexiv sind. Ebenso gibt es Relationen, die weder symmetrisch noch antisymmetrisch sind, und Relationen, die gleichzeitig symmetrisch und antisymmetrisch sind (siehe Beispiele unten). Insofern verhalten sich die Begriffe nicht komplementär zueinander. Wir können nicht folgern: Die Relation ist nicht symmetrisch, also ist sie antisymmetrisch.
Beispiel: Sei A = {1, 2, 3}. Die folgenden Mengen R1, R2 und R3 sind Relationen auf A, und es gilt
R1 = { (1, 1), (1, 2) } ist nicht reflexiv und nicht irreflexiv,
R2 = { (1, 2), (2, 1), (1, 3) } ist nicht symmetrisch und nicht antisymmetrisch,
R3 = { (2, 2), (3, 3) } ist symmetrisch und antisymmetrisch.
Ordnungs- und Äquivalenzrelation
Definition: Eine Relation heißt Halbordnung, wenn sie reflexiv, antisymmetrisch und transitiv ist.
Eine Relation heißt strenge Halbordnung, wenn sie irreflexiv und transitiv ist.1)
Eine Relation heißt lineare Ordnung oder totale Ordnung oder Ordnung, wenn sie Halbordnung ist und zusätzlich noch total ist.
Eine Relation heißt Äquivalenzrelation, wenn sie reflexiv, symmetrisch und transitiv ist.
Beispiel: Die Relationen ≤ und | ("teilt") auf ℕ sind Halbordnungen, ≤ ist sogar totale Ordnung.
Die Relation ≡ n ("ist kongruent modulo n", d.h. liefert bei ganzzahliger Division durch n denselben Rest) ist eine Äquivalenzrelation auf ℤ.
Die Relation 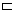auf der Menge der Menschen M ist eine strenge Halbordnung. Die Relation ~ auf M ist eine Äquivalenzrelation.
Äquivalenzrelationen auf einer Menge A bewirken eine Klasseneinteilung von A, d.h. eine Zerlegung von A in paarweise disjunkte Mengen (Äquivalenzklassen).
Die Äquivalenzrelation ≡ 2 bewirkt eine Klasseneinteilung von ℤ in die geraden und die ungeraden Zahlen. Die Äquivalenzklassen der Relation ~ auf der Menge der Menschen sind die Geschwister.
Operationen auf Relationen
Definition: Das Produkt zweier Relationen R, T ⊆ A × A ist die Relation
RT = { (a, c) | ∃ b ∈ A : (a, b) ∈ R ∧ (b, c) ∈ T }
Potenzen einer Relation R ⊆ A × A sind wie folgt definiert:
R0 = { (a, a) | a ∈ A }
Ri = Ri-1 R für alle i ∈ ℕ
Definition: Die transitive Hülle einer Relation R ist die Relation
R+ = 
i ∈ IN Ri = R ∪ R2 ∪ R3 ∪ . . .
Die reflexive Hülle einer Relation R ist die Relation
R? = R0 ∪ R.
Die reflexive und transitive Hülle einer Relation R ist die Relation
R* = i ∈ IN0 Ri = R0 ∪ R+
Die Hülle einer Relation R bezüglich einer Eigenschaft ergibt sich, indem die fehlenden Elemente hinzugenommen werden. D.h. die Hülle ist die kleinste Relation, die R umfasst und die betreffende Eigenschaft hat.
Aus einer strengen Halbordnung R lässt sich eine Halbordnung H machen, indem die reflexive Hülle H = R0 ∪ R gebildet wird. Umgekehrt ergibt sich die zu einer Halbordnung H gehörige strenge Halbordnung R, indem R = H \ H0 gebildet wird.
Definition: Die inverse Relation von R ⊆ A × A ist die Relation
R -1 = { (b, a) | (a, b) ∈ R }
Beispiel: Sei M die Menge der Menschen und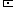 
die Relation "ist Elternteil von" auf M. Die Relation 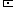-1 bedeutet dann "ist Kind von", die Relation 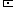2 bedeutet "ist Großelternteil von" und die Relation 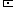+ ist identisch mit der Relation 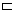("ist Elternteil oder Großelternteil oder Urgroßelternteil oder ..., d.h. ist Vorfahre von").
Das Produkt der Relationen 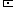("ist Elternteil von") und 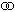("ist verheiratet mit") ist die Relation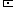 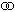. Zwei Menschen a und c stehen in der Relation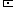 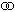, wenn es einen Menschen b gibt, sodass a Elternteil von b ist und b mit c verheiratet ist. Damit ist a Schwiegermutter oder Schwiegervater von c.
Aufgaben
Aufgabe 1: Eine strenge Halbordnung ist irreflexiv und transitiv. Zeigen Sie, indem Sie die Definitionen dieser Eigenschaften heranziehen, dass jede strenge Halbordnung antisymmetrisch ist.
Aufgabe 2: Offenbar gilt für eine Relation R auf einer Menge A
R ist reflexiv ⇔ R0 ⊆ R
Charakterisieren Sie auf ähnliche Weise mithilfe von Ri:
- R ist symmetrisch
- R ist transitiv
- R ist irreflexiv
Literatur
Die Mathematik, die Sie in der Informatik brauchen, finden Sie beispielsweise in folgenden Büchern. Wenn Sie noch am Anfang stehen, ist empfehlenswert:
[Lan 21] H.W. Lang: Vorkurs Informatik für Dummies. Wiley (2021)
Lesen Sie zum Thema Relationen auch Kapitel 14 in meinem Buch Vorkurs Informatik für Dummies.
1) Der Begriff "strenge Halbordnung" ist etwas unglücklich, da er wie "Halbordnung, und zusätzlich noch streng" klingt. Tatsächlich ist aber eine strenge Halbordnung nicht reflexiv und daher keine Halbordnung im Sinne der obigen Definition, sondern eine "andere Art von Halbordnung".
Weiter mit: [Abbildung] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 15.09.1997 Updated: 11.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden