Mathematische Grundlagen
Abbildung
Abbildungen sind spezielle zweistellige Relationen. Während eine Relation eine völlig beliebige Teilmenge eines kartesischen Produktes ist, werden an eine Abbildung zwei bestimmte Bedingungen gestellt. Dies kommt in der folgenden Definition zum Ausdruck.
Definition
Definition: Seien A und B Mengen. Eine Abbildung ist eine Relation f ⊆ A × B mit den folgenden Eigenschaften (1) und (2). Wegen der Gültigkeit dieser Eigenschaften ist bei Abbildungen folgende Schreibweise üblich:
| f : A → B | statt | f ⊆ A × B | und | |||
| f(a) = b | statt | (a, b) ∈ f. |
Die Menge A wird in die Menge B abgebildet. Jedes Element a ∈ A wird auf irgendein Element b ∈ B abgebildet, dabei heißt b das Bild von a unter der Abbildung f.
Die folgende Eigenschaft (1) besagt, dass wenn zwei Elemente gleich sind, auch die entsprechenden Bilder gleich sind. Kein Element wird also gleichzeitig auf zwei verschiedene Bilder abgebildet, das Bild ist immer eindeutig.
(1) eindeutig
∀ a, a' ∈ A : a = a' ⇒ f(a) = f(a')
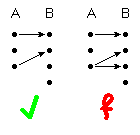
(von jedem Punkt geht höchstens ein Pfeil aus)
Die Eigenschaft (2) besagt, dass jedes Element a ∈ A ein Bild hat.
(2) total definiert
∀ a ∈ A ∃ b ∈ B : f(a) = b
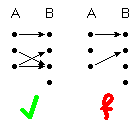
(von jedem Punkt geht mindestens ein Pfeil aus)
(1) und (2) zusammen ergeben: Von jedem Punkt geht genau ein Pfeil aus (die Abbildung ist wohldefiniert). Eine Relation, die nur (1) erfüllt, wird als partielle Abbildung bezeichnet.
(1) + (2) Abbildung
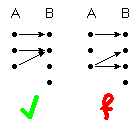
(von jedem Punkt geht genau ein Pfeil aus)
Genau wie eine Relation ist also eine Abbildung nichts anderes als eine Menge von Paaren, die allerdings die genannten Bedingungen (1) und (2) erfüllen muss. Ein anderes Wort für Abbildung ist Funktion. Gelegentlich trifft man auf Formulierungen wie "die Funktion y = 3x2 ". Gemeint ist hierbei "die Funktion mit der Funktionsgleichung y = 3x2 ", und dies ist die Menge { (x, y) | y = 3x2}, also die Menge aller Paare (x, y), die der Funktionsgleichung genügen.
Injektitiv, surjektiv, bijektiv
Definition: Sei f : A → B eine Abbildung, d.h. f erfüllt (1) und (2). Die Abbildung f heißt injektiv, wenn f die folgende Eigenschaft (3) hat; f heißt surjektiv, wenn f die folgende Eigenschaft (4) hat; f heißt bijektiv, wenn f beide Bedingungen (3) und (4) erfüllt.
Die folgende Eigenschaft (3) besagt, dass wenn zwei Elemente verschieden sind, auch die entsprechenden Bilder verschieden sind.
(3) injektiv
∀ a, a' ∈ A : a ≠ a' ⇒ f(a) ≠ f(a')
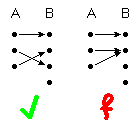
(bei jedem Punkt kommt höchstens ein Pfeil an)
Die Eigenschaft (4) besagt, dass jedes Element b ∈ B ein Bild ist (d.h. ein Urbild hat).
(4) surjektiv
∀ b ∈ B ∃ a ∈ A : f(a) = b
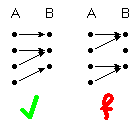
(bei jedem Punkt kommt mindestens ein Pfeil an)
(3) und (4) zusammen ergeben: Bei jedem Punkt kommt genau ein Pfeil an (die Abbildung ist bijektiv). Dies bedeutet, dass die inverse Relation f -1 der Abbildung f auch eine Abbildung ist (sogar ebenfalls eine bijektive Abbildung).
(3) + (4) bijektiv
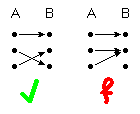
(bei jedem Punkt kommt genau ein Pfeil an)
Tatsächlich wissen schon kleine Kinder, was eine bijektive Abbildung ist. Beim Zählen nämlich kommt es darauf an, eine bijektive Abbildung herzustellen zwischen der Menge der Gegenstände, die gezählt werden sollen, und der Menge {1, ..., n} (vergl. nächster Abschnitt: Mächtigkeit einer Menge). Sollen beispielsweise Stofftiere gezählt werden, so stellt das Kind die Abbildung her, indem es unter Beachtung der Bedingungen (1) bis (4) jeweils auf ein Stofftier zeigt und dabei eine Zahl sagt.
Ganz kleine Kinder, die noch nicht richtig zählen können, verletzen regelmäßig mindestens eine der Bedingungen (1) bis (4). So zeigt das Kind etwa mehrfach auf ein Stofftier oder vergisst eines. Oder es zeigt zwar auf alle Stofftiere, sagt dabei aber die Zahlen "1, 2, 2, 3, 4". Oder es sagt die Zahlen "1, 2, 5, 6, 8".
Mächtigkeit
Definition: Die Mächtigkeit |A| einer Menge A ist wie folgt definiert:
| |A| = | 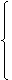 |
|
Eine Menge mit der Mächtigkeit n ∈ ℕ0 heißt endliche Menge. Bei endlichen Mengen ist die Mächtigkeit gleich der Anzahl der Elemente. Eine Menge, die nicht endlich ist, heißt unendliche Menge.
Bei unendlichen Mengen kann man den Begriff der Mächtigkeit nicht mehr anschaulich mit der Anzahl der Elemente verbinden. So sind etwa die Mengen ℕ und ℤ gleich mächtig, obwohl ℕ anschaulich "weniger" Elemente enthält als ℤ. Andererseits sind auch wieder nicht alle unendlichen Mengen gleich mächtig.
Definition: Zwei Mengen A und B sind gleich mächtig, wenn es eine bijektive Abbildung zwischen ihnen gibt:
|A| = |B| ⇔ ∃ bijektive Abbildung f : A ⟷ B
Offenbar gibt es eine bijektive Abbildung zwischen ℕ und ℤ, etwa gemäß folgender Wertetabelle:
Andererseits gibt es keine bijektive Abbildung zwischen den unendlichen Mengen ℕ und ℝ, daher sind diese beiden Mengen nicht gleich mächtig. Es gibt also offenbar verschiedene Grade des Unendlichen.
Die Mächtigkeit ℵ0 wird als abzählbar unendlich bezeichnet. Eine Menge ist abzählbar unendlich, wenn sie gleich mächtig zu den natürlichen Zahlen ist. Die Bezeichnung ℵ0 geht auf Cantor zurück. Das Zeichen ℵ (aleph) ist der erste Buchstabe des hebräischen Alphabets. Die Mächtigkeit ℵ0 ist die kleinste Mächtigkeit, die eine unendliche Menge haben kann.
Eine Menge, die entweder endlich oder abzählbar unendlich ist, wird als abzählbar bezeichnet. Offenbar ist eine Menge M abzählbar, wenn es eine surjektive Abbildung von ℕ auf M gibt.
Eine unendliche Menge, die nicht abzählbar unendlich ist, wird als überabzählbar unendlich bezeichnet. So ist beispielsweise ℝ überabzählbar unendlich. Das Zeichen 𝔠 bedeutet "Mächtigkeit des Kontinuums".
Beispiel: Einige Beispiele für die Mächtigkeit von Mengen:
| {1, 2, 5, 7} | = 4
| {2, 4, 6, 8, ... } | = ℵ0
|ℤ| = ℵ0
|ℚ| = ℵ0
| [0,1] | = 𝔠
|ℂ| = 𝔠
|ℝn| = 𝔠
| (ℕ)| = 𝔠
(ℕ)| = 𝔠
Folge
Definition: Sei A eine Menge. Unter einer Folge versteht man eine Abbildung
a : ℕ0 → A.
Eine endliche Folge ist eine Abbildung
a : {0, ..., n-1} → A, n ∈ ℕ0.
Hierbei ist n die Länge der endlichen Folge.
Wir schreiben endliche Folgen so: a = a0, ..., an-1. Endliche Folgen lassen sich auch als n-Tupel (a0, ..., an-1) auffassen, d.h. als Elemente des kartesischen Produktes An.
Permutation
Definition: Eine Permutation ist eine bijektive Abbildung
p : {0, ..., n-1} → {0, ..., n-1}, n ∈ ℕ.
Beispiel: Die endliche Folge p = 4, 1, 2, 0, 3 ist eine Permutation.
Literatur
Die Mathematik, die Sie in der Informatik brauchen, finden Sie beispielsweise in folgenden Büchern. Wenn Sie noch am Anfang stehen, ist empfehlenswert:
[Lan 21] H.W. Lang: Vorkurs Informatik für Dummies. Wiley (2021)
Zum Thema Abbildungen lesen Sie Kapitel 15 in meinem Buch Vorkurs Informatik für Dummies.
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 15.04.2014 Updated: 11.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden
