Transformationen
Transformation
Gelegentlich ist es vorteilhafter, ein Problem über einen Umweg zu lösen, als es auf direktem Wege zu lösen.
Weihnachtsstern basteln
Bild 1 zeigt den untauglichen Versuch, einen Stern auf direktem Wege auszuschneiden.

Bild 1: Direkte Lösung
Der indirekte Weg besteht darin, das Papier zunächst zu falten. Dann wird eine Ecke in das gefaltete Papier geschnitten. Zum Schluss wird das Papier wieder auseinandergefaltet. Das Ergebnis ist ein perfekt regelmäßiger Stern (Bild 2).



Bild 2: Indirekte Lösung
Der indirekte Weg besteht darin, dass die ursprüngliche Aufgabe transformiert wird. Es entsteht eine neue, gänzlich anders geartete Aufgabe, die leichter zu lösen ist. Zum Schluss wird eine Rücktransformation vorgenommen, um aus der Lösung des transformierten Problems die Lösung des ursprünglichen Problems zu gewinnen. Bild 3 zeigt schematisch diese Vorgehensweise.
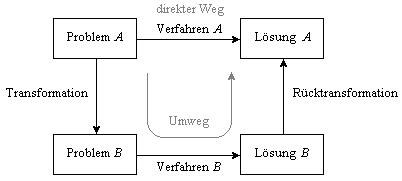
Bild 3: Indirekte Lösung eines Problems durch Transformation
Rechnen mit Logarithmen
Als es noch keine Taschenrechner gab, wurde in der Schule das Rechnen mit Logarithmen gelehrt.
Hierbei werden zwei Zahlen miteinander multipliziert, indem zunächst ihre Logarithmen aus einer Logarithmentafel herausgesucht werden (Transformation). Die Logarithmen werden addiert (Verfahren B). Zu diesem Ergebnis wird nun umgekehrt die zugehörige Zahl, also der inverse Logarithmus, aus der Logarithmentafel herausgesucht (Rücktransformation). Diese Zahl ist das Produkt der Zahlen. Die Rechnung basiert auf der Beziehung
log(a·b) = log(a) + log(b)
Der Umweg über die Logarithmentafel lohnt sich dann, wenn der Aufwand für das Heraussuchen der Logarithmen, die anschließende Addition sowie das Heraussuchen des inversen Logarithmus schneller geht als die direkte Multiplikation. Wirklich effizient ist das Rechnen mit Logarithmen nur, wenn längere Rechnungen mit mehreren Multiplikationen und insbesondere mit Potenzen und Wurzeln auszuführen sind.
Montgomery-Multiplikation
Ein ähnliches Beispiel aus dem Bereich der ganzen Zahlen ist die Montgomery-Multiplikation. Das zu lösende Problem besteht in der Multiplikation zweier ganzer Zahlen a und b modulo einer Zahl n:
c = a · b mod n
Zum Beispiel gilt 3 · 5 mod 7 = 1, denn 3 · 5 = 15 ergibt bei ganzzahliger Division durch 7 den Rest 1.
Die direkte Berechnung erfordert eine Division durch n; diese Operation ist aufwendig, insbesondere bei sehr großen Zahlen, die typischerweise in der Kryptografie verwendet werden.
Bei der Montgomery-Multiplikation werden die beteiligten Zahlen mit einer Transformation h so transformiert, dass anstelle der Division durch n eine Division durch eine Zweierpotenz m möglich ist. Eine Division durch eine Zweierpotenz lässt sich bei binärer Zahlendarstellung durch eine wesentlich weniger aufwendige Schiebeoperation realisieren.
Auch hier gilt, dass sich die Transformation nur lohnt, wenn längere Rechnungen mit mehreren Multiplikationen und mit Potenzen auszuführen sind.
Polynommultiplikation
Die Polynommultiplikation lässt sich mithilfe der Schnellen Fouriertransformation beschleunigen. Statt zwei Polynome vom Grad n auf direktem Wege in Zeit Θ(n2) zu multiplizieren, werden die Polynome zunächst an 2n jeweils gleichen Stützstellen ausgewertet, dann werden die jeweils 2n Funktionswerte miteinander multipliziert, und zum Schluss wird aus diesen 2n Werten durch Interpolation das Ergebnispolynom berechnet.
Durch Anwendung der Schnellen Fouriertransformation benötigen Auswertung und Interpolation jeweils Zeit O(n log(n)). Die Multiplikation der Funktionswerte benötigt Zeit O(n). Insgesamt ergibt sich für die Polynommultiplikation auf diesem indirekten Wege somit eine Zeitkomplexität von O(n log(n)).
Reduktion
Eine weitere wichtige Anwendung der Transformation ist die Reduktion. Wenn es möglich ist, den Umweg in Bild 3 zu gehen, so lässt sich Problem A auf Problem B reduzieren.
Dies ist dann interessant, wenn beispielsweise kein direktes Verfahren zur Lösung von Problem A bekannt ist. Wenn sich aber Problem A auf Problem B reduzieren lässt und für Problem B ein Lösungsverfahren bekannt ist, ergibt sich somit ein indirektes Verfahren zur Lösung von Problem A.
Durch Reduktion eines Problems auf ein anderes Problem lassen sich auch oft obere und untere Schranken für die Komplexität der Probleme gewinnen.
Obere Schranken
Hat beispielsweise Problem B polynomielle Komplexität, d.h. T(n) ∈ O(nk), und lässt sich Problem A auf Problem B polynomiell reduzieren (d.h. Transformation und Rücktransformation haben ebenfalls polynomielle Komplexität), so hat Problem A ebenfalls polynomielle Komplexität.
Aus einer oberen Schranke von Problem B lässt sich also unter diesen Bedingungen eine obere Schranke für Problem A gewinnen.
Untere Schranken
Kennt man dagegen eine untere Schranke für Problem A, etwa Ω(f(n)), so muss auch der Umweg über ein Problem B in Ω(f(n)) liegen. Denn ginge der Umweg schneller, so könnte man ihn beschreiten – damit wäre aber Ω(f(n)) keine untere Schranke für Problem A mehr.
Ein Beispiel für diese Vorgehensweise ist die Bestimmung der unteren Schranke für die Berechnung der konvexen Hülle von n Punkten. Es lässt sich nämlich das Sortierproblem (Problem A) auf das Problem der Berechnung der konvexen Hülle (Problem B) reduzieren. Das Sortierproblem hat eine untere Schranke von Ω(n log(n)). Somit ist Ω(n log(n)) auch eine untere Schranke für den Umweg über Problem B. Transformation und Rücktransformation liegen in O(n), sind also nicht verantwortlich für die Komplexität des Umwegs. Also muss Problem B selber, also das Problem der Berechnung der konvexen Hülle, eine Komplexität von Ω(n log(n)) haben.
Weiter mit: [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 15.01.2003 Updated: 08.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden