Transformationen
Transformation von Polynomen
Polynomauswertung
Gegeben sei ein Polynom
p(x) = a0·x0 + a1·x1 + a2·x2 + ... + an-1·xn-1.
Die Berechnung des Wertes p(x0) an einer Stelle x0 wird als Polynomauswertung bezeichnet. Der Wert p(x0) ergibt sich, indem der Wert x0 für die Variable x eingesetzt wird und die im Polynom vorkommenden Rechenoperationen ausgeführt werden.
Beispiel: Es sei p(x) = 5·x0 + 7·x1 + 3·x2. Die Auswertung von p(x) an der Stelle x0 = 2 ergibt
p(2) = 5·1 + 7·2 + 3·4 = 5 + 14 + 12 = 31
oder in Vektorschreibweise
| 31 = | [5 7 3] · |
|
Allgemein ist in Vektorschreibweise der Wert y0 = p(x0) gleich dem Produkt
| y0 = | [a0 ... an-1] · |
|
Bei Auswertung des Polynoms an n Stellen x0, ..., xn-1 ergibt sich ein Ergebnisvektor [y0 ... yn-1], und die Berechnung entspricht einer Vektor-Matrix-Multiplikation
| [y0 ... yn-1] = | [a0 ... an-1] · |
|
oder kürzer
y = a·T
Die Matrix T ist die Transformationsmatrix. Sie ist eine sogenannte Vandermonde-Matrix der Werte x0, ..., xn-1.
Polynominterpolation
Sind die n Stellen x0, ..., xn-1 alle verschieden, so ist die Transformationsmatrix T invertierbar. Dann können die Koeffizienten des Polynoms aus den n Werten y0, ..., yn-1 in eindeutiger Weise zurückberechnet werden:
a = y·T -1
Die Berechnung der Koeffizienten eines Polynoms, dessen Werte an n verschiedenen Stellen gegeben sind, heißt Polynominterpolation.
Es ist also möglich, n Punkte in der Ebene, deren x-Werte verschieden sind, durch ein Polynom vom Grad < n zu interpolieren. Für den Fall n = 2 ist dies wohlbekannt, denn durch zwei Punkte verläuft genau eine Gerade, und die Gleichung einer Geraden ist ein Polynom vom Grad < 2.
Tatsächlich aber verläuft auch durch drei Punkte genau eine Kurve, die einem Polynom vom Grad < 3 entspricht, also eine Parabel. Durch vier Punkte verläuft genau eine Kurve, die einem Polynom vom Grad < 4 entspricht, usw.
Bild 1 zeigt vier Punkte und die Interpolation durch ein Polynom vom Grad < 4.
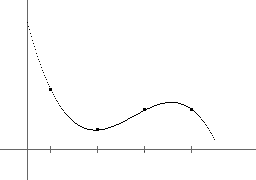
Bild 1: Interpolation durch ein Polynom
Koeffizienten- und Stützstellendarstellung
Ein Polynom vom Grad < n lässt sich als gewichtete Summe der n fest vorgegebenen Basisfunktionen bi(x) = xi mit i = 0, ..., n-1 auffassen. Die Gewichte, mit denen die Basisfunktionen in die Summe eingehen, sind die Koeffizienten des Polynoms. Durch Angabe der entsprechenden Koeffizienten a0, ..., an-1 lässt sich das Polynom eindeutig darstellen. Diese Darstellung heißt Koeffizientendarstellung des Polynoms.
Wenn nun n verschiedene Stellen x0, ..., xn-1 fest vorgegeben sind und das Polynom an diesen Stellen ausgewertet wird, so ergeben sich die Ergebnisse y0, ..., yn-1. Es stellt sich heraus, dass sich das Polynom durch Angabe dieser Ergebnisse ebenfalls eindeutig darstellen lässt. Die Darstellung des Polynoms durch y0, ..., yn-1 heißt Stützstellendarstellung des Polynoms.
Wie eben gesehen, lässt sich die Stützstellendarstellung des Polynoms aus der Koeffizientendarstellung durch Multiplikation mit einer Matrix T gewinnen:
[y0 ... yn-1] = [a0 ... an-1] · T
und umgekehrt die Koeffizientendarstellung aus der Stützstellendarstellung durch Multiplikation mit der inversen Matrix T -1
[a0 ... an-1] = [y0 ... yn-1] · T -1
Es lässt sich also zwischen den beiden Darstellungen hin- und zurückrechnen.
Wahl der Basisfunktionen und der Stützstellen
Die Transformationsmatrix T ist abhängig von den Basisfunktionen bi(x) und von den Stützstellen xj, wobei i, j = 0, ..., n-1, und zwar ist allgemein
Ti,j = bi(xj).
Eine invertierbare Transformationsmatrix T ergibt sich, wenn die Basisfunktionen linear unabhängig sind (was bei bi(x) = xi der Fall ist) und die Stützstellen alle verschieden sind.
Statt der Potenzfunktionen xi lassen sich auch andere Funktionen als Basisfunktionen bi(x) verwenden. So werden etwa bei der diskreten Kosinustransformation die Basisfunktionen bi(x) = cos (i·x) verwendet.1)
Durch Verwendung anderer Basisfunktionen kommt eine andere Art der Interpolation zustande. Bild 2 zeigt die Interpolation von zwei Punkten
- durch die Summe der Basisfunktionen x0 und x1, d.h. durch ein Polynom vom Grad < 2 (eine Gerade) und
- durch die Summe der Basisfunktionen cos(0·x) und cos(1·x), d.h. durch eine diskrete Kosinustransformation.
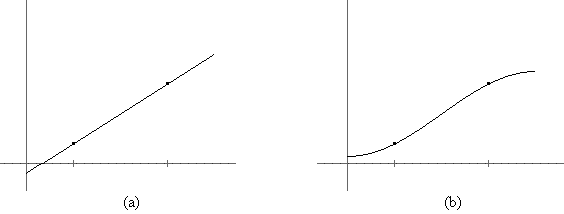
Bild 2: Interpolation durch ein Polynom (a) und durch Kosinusfunktionen (b)
Bei der diskreten Fouriertransformation werden die Potenzfunktionen xi als Basisfunktionen bi(x) verwendet und als Stützstellen xj die komplexen Werte
cos(j·2π/n) + isin(j·2π/n) = ei·j·2π/n
mit i, j = 0, ..., n-1. 2)
Polynommultiplikation
Die Multiplikation eines Polynoms vom Grad k mit einem Polynom vom Grad m ergibt ein Polynom vom Grad n = k+m. Sind die Polynome in Koeffzientendarstellung gegeben, so erfordert das direkte Ausmultiplizieren der Polynome Θ(k·m) Operationen. Im schlechtesten Fall, wenn k = m = n/2 ist, sind dies also Θ(n2) Operationen.
Sind dagegen die Polynome in Stützstellendarstellung gegeben, so dauert die Multiplikation nur Θ(n) Schritte. Voraussetzung ist dabei allerdings, dass die Stützstellen xi beider Polynome übereinstimmen und dass n Stützstellen vorliegen, wenn das Ergebnispolynom den Grad n-1 hat.
Sind y0, ..., yn-1 und z0, ..., zn-1 die Stützstellendarstellungen zweier Polynome p und q mit grad(p) + grad(q) < n, so ist y0·z0, ..., yn-1·zn-1 die Stützstellendarstellung des Produkts der beiden Polynome. Es sind also nur die n Werte an den Stützstellen miteinander zu multiplizieren.
Die Idee liegt nahe, die Polynommultiplikation zu beschleunigen, indem die Polynome zunächst von der Koeffizientendarstellung in Stützstellendarstellung umgeformt werden und dann multipliziert werden. Aber leider scheint die Umformung bereits Θ(n2) Zeit zu dauern, also genauso lange wie die direkte Multiplikation in Koeffizientendarstellung.
Tatsächlich jedoch gibt es eine Methode zur Umformung von Koeffizientendarstellung in Stützstellendarstellung, die nur Zeit O(n log(n)) benötigt: die schnelle Fouriertransformation (engl.: Fast Fourier Transform – FFT). Der Trick dieser Methode besteht darin, die Symmetrie der Stützstellen, die bei der Fouriertransformation verwendet werden, auszunutzen. Dadurch vereinfacht sich die Berechnung. Bild 3 zeigt, wie mit Hilfe der FFT die Polynommultiplikation über den Umweg der Stützstellendarstellung beschleunigt werden kann.
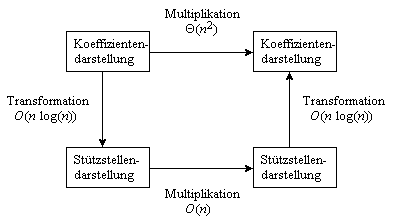
Bild 3: Polynommultiplikation: direkt und indirekt über FFT
1) Aus praktischen Gründen werden die Funktionen bi noch mit einem konstanten Faktor si skaliert.
2) i =  -1 ist die imaginäre Einheit.
-1 ist die imaginäre Einheit.
Weiter mit: [Schnelle Fouriertransformation (FFT)] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 08.11.2001 Updated: 08.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden