Transformationen
Schnelle Fouriertransformation (FFT)
Die Fouriertransformation ist ein fundamentales Verfahren in der Signalverarbeitung. Durch die Fouriertransformation lassen sich Signale von der Darstellung {(Zeitpunkt, Abtastwert)} in die Darstellung {(Frequenzanteil, Amplitude, Phase)} überführen. Viele Operationen, z.B. Filter, lassen sich im Frequenzraum leichter durchführen. Anschließend wird das Signal mit der inversen Fouriertransformation wieder zurück transformiert. [Beispiel]
Außerdem hat die Fouriertransformation Anwendungen in der Numerik; z.B. lässt sich eine Polynommultiplikation schneller durchführen, wenn die Polynome in Stützstellendarstellung statt in Koeffizientendarstellung vorliegen.
Das Verfahren der schnellen Fouriertransformation (engl.: Fast Fourier Transform – FFT) hat eine Zeitkomplexität von Θ(n log(n)). Dadurch ist die Polynommultiplikation sogar einschließlich Transformation in Stützstellendarstellung und Rücktransformation noch schneller als die direkte Multiplikation in Koeffizientendarstellung.
Grundlagen
Definition: Sei ℂ der Körper der komplexen Zahlen. Ein Element w ∈ ℂ heißt n-te Einheitswurzel, wenn wn = 1 ist, und w heißt primitive n-te Einheitswurzel, wenn wn = 1 ist, aber wk ≠ 1 für alle k ∈ {1, ..., n-1}.
Beispiel: Sei n = 4. Dann ist i primitive 4-te Einheitswurzel1). Alle 4-ten Einheitswurzeln sind:
i0 = 1, i1 = i, i2 = -1, i3 = -i
Für n = 6 ist cos(2π/6) + i sin(2π/6) primitive 6-te Einheitswurzel (Bild 1).
Allgemein gilt in ℂ:
w = cos(k·2π/n) + i sin(k·2π/n) mit k ∈ {0, ..., n-1}
ist n-te Einheitswurzel; ist k teilerfremd zu n, so ist w primitiv.
In der eulerschen Schreibweise lässt sich eine n-te Einheitswurzeln w auch ausdrücken als
w = eik2π/n mit k ∈ {0, ..., n-1}.
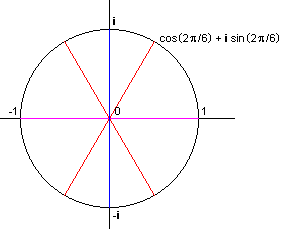
Bild 1: Einheitskreis in der gaußschen Zahlenebene mit 4-ten und 6-ten Einheitswurzeln
Eigenschaften von n-ten Einheitswurzeln
- Es gibt in ℂ genau n verschiedene n-te Einheitswurzeln, diese sind darstellbar als die Potenzen einer primitiven n-ten Einheitswurzel w:
w0, w1, w2, ..., wn-1
- Jede ganzzahlige Potenz wk einer n-ten Einheitswurzel w ist wieder n-te Einheitswurzel, denn
(wk)n = wk·n = (wn)k = 1k = 1
Dies gilt auch für negative k.
- Ist n gerade, so gilt für jede primitive n-te Einheitswurzel w:
wn/2 = -1,
denn (wn/2)2 = wn = 1, d.h. wn/2 ist 2-te Einheitswurzel, also 1 oder -1. Da aber wn/2 ≠ 1 ist, da w primitiv ist, gilt wn/2 = -1.
- Das Quadrat w2 einer primitiven n-ten Einheitswurzel (n gerade) ist primitive n/2-te Einheitswurzel, denn
- (w2)n/2 = wn = 1.
- Angenommen, w2 sei nicht primitiv, dann existiert ein k ∈ {1, ..., n/2-1} mit (w2)k = 1. Dann ist aber w2k = 1 mit 2k < n, im Widerspruch dazu, dass w primitiv ist.
- Ist w primitive n-te Einheitswurzel, so ist w-1 ebenfalls primitive n-te Einheitswurzel, denn
- (w-1)n = w-n = 1/wn = 1/1 = 1.
- Angenommen, w-1 sei nicht primitiv, dann existiert ein k ∈ {1, ..., n-1} mit (w-1)k = w-k = 1. Dann ist aber wk = 1/w-k = 1/1 = 1, im Widerspruch dazu, dass w primitiv ist.
- In ℂ gilt für die zu einer n-ten Einheitswurzel w konjugierte Zahl w
w = w-1
denn es ist
w · w = (cos(k·2π/n) + i sin(k·2π/n)) · (cos(k·2π/n) – i sin(k·2π/n)) = cos(k·2π/n)2 + sin(k·2π/n)2 = 1.
Diskrete Fouriertransformation
Die diskrete Fouriertransformation ist definiert als eine Vektor-Matrix-Multiplikation.
Definition: Sei n ∈ ℕ und w primitive n-te Einheitswurzel in ℂ. Eine n × n-Matrix F mit
Fi,j = wi·j
für alle i, j ∈ {0, ..., n-1} heißt Fouriermatrix.2)
Die lineare Abbildung f : ℂn → ℂn mit
f(a) = a·F
für alle (Zeilen-)vektoren a ∈ ℂn heißt diskrete Fouriertransformation (DFT).3)
Beispiel: Sei n = 4. Dann ist i primitive n-te Einheitswurzel. Die zugehörige Fouriermatrix ist
| F = | 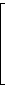 |
| 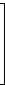 |
So ist etwa die -1 in der letzten Zeile der Matrix das Element
F3,2 = w3·2 = w6 = (-1)3 = -1
(die Elemente der Matrix werden von 0 bis n-1 indiziert).
Die Fouriertransformation des Vektors a = [1 1 1 0] ergibt
y = a·F = [3 i 1 -i]
Inverse Fouriertransformation
Satz: Die inverse Fouriermatrix F -1 existiert und ist gleich
F -1i,j = 1/n · w-i·j
für alle i, j ∈ {0, ..., n-1}. Die inverse Fouriermatrix enthält also die zu den Elementen der Fouriermatrix inversen Elemente, dividiert durch n.
Definition: Die lineare Abbildung f -1 : ℂn → ℂn mit
f -1(a) = a·F -1
für alle a ∈ ℂn heißt inverse Fouriertransformation.
Beispiel: Sei n = 4. Die inverse Fouriermatrix ist
| F -1 = 1/4 · | 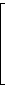 |
| 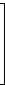 |
Die inverse Fouriertransformation des Vektors y = [3 i 1 -i] ergibt
a = y·F -1 = [1 1 1 0].
Interpretation als Polynomauswertung
Offenbar ist die Fouriermatrix F die Vandermonde-Matrix des Vektors w0, ..., wn-1. Die Matrix-Vektor-Multiplikation y = a·F lässt sich somit als Polynomauswertung an den Stellen w0, ..., wn-1 auffassen, wobei der Vektor a die Koeffizienten des Polynoms enthält (Koeffizient von x0 zuerst). Das Ergebnis y0, ..., yn-1 ist die Stützstellendarstellung des Polynoms.
Mit der inversen Fouriertransformation wird das Polynom von der Stützstellendarstellung wieder in die Koeffizientendarstellung zurückverwandelt.
In dieser Form ist die Fouriertransformation eine Matrix-Vektor-Multiplikation mit der Komplexität Θ(n2). Durch Ausnutzung der Symmetrie der n-ten Einheitswurzeln lässt sich die Berechnung auf Θ(n log(n)) beschleunigen. Dieses Verfahren heißt schnelle Fouriertransformation (Fast Fourier Transform – FFT) [CT 65].
Schnelle Fouriertransformation (FFT)
Die Idee des Verfahrens der schnellen Fouriertransformation ist, die einzelnen Berechnungen der Matrix-Vektor-Multiplikation y = a·F in einer speziellen Reihenfolge auszuführen, sodass jeweils auf schon berechnete Zwischenergebnisse zurückgegriffen werden kann. Dabei werden die o.a. Eigenschaften (3) und (4) ausgenutzt, nämlich dass wn/2 = -1 ist und dass das Quadrat w2 der primitiven n-ten Einheitswurzel w primitive n/2-te Einheitswurzel ist. Das Verfahren setzt voraus, dass n eine Zweierpotenz ist.
Komponenten von y mit geradem Index
Zunächst werden die Komponenten von y mit geradem Index berechnet, indem der Vektor a mit den entsprechenden Spalten der Fouriermatrix multipliziert wird. Es gilt für alle k ∈ {0, ..., n/2-1}:
yk' = y2k =  i = 0, ..., n-1 ai wi·2k
i = 0, ..., n-1 ai wi·2k
Die Summe wird in zwei Hälften aufgespalten:
yk' =  i = 0, ..., n/2-1 ai wi·2k +
i = 0, ..., n/2-1 ai wi·2k +  i = 0, ..., n/2-1 ai+n/2 w(i+n/2)·2k
i = 0, ..., n/2-1 ai+n/2 w(i+n/2)·2k
Nun ist aber
w(i+n/2)·2k = wi·2k + nk = wi·2k·wnk = wi·2k
da wnk = 1 ist, und damit
yk' =  i = 0, ..., n/2-1 (ai + ai+n/2) wi·2k
i = 0, ..., n/2-1 (ai + ai+n/2) wi·2k
Mit m = n/2 sowie v = w2, v primitive m-te Einheitswurzel, gilt:
yk' =  i = 0, ..., m-1 (ai + ai+m) vi·k
i = 0, ..., m-1 (ai + ai+m) vi·k
d.h. yk' ist nichts anderes als die k-te Komponente der Fouriertransformation des Vektors
(ai + ai+m) i = 0, ..., m-1
der Länge m.
Komponenten von y mit ungeradem Index
Ähnlich werden die Komponenten von y mit ungeradem Index berechnet. Es gilt für alle k ∈ {0, ..., n/2-1} :
yk'' = y2k+1 =  i = 0, ..., n-1 ai wi·(2k+1)
i = 0, ..., n-1 ai wi·(2k+1)
Wiederum wird die Summe in zwei Hälften aufgespalten:
yk'' =  i = 0, ..., n/2-1 ai wi·(2k+1) +
i = 0, ..., n/2-1 ai wi·(2k+1) +  i = 0, ..., n/2-1 ai+n/2 w(i+n/2)·(2k+1)
i = 0, ..., n/2-1 ai+n/2 w(i+n/2)·(2k+1)
Nun ist aber
w(i+n/2)·(2k+1) = wi·2k + nk + i + n/2 = - wi·wi·2k
da wnk = 1 ist und wn/2 = -1 ist. Somit gilt:
yk'' =  i = 0, ..., n/2-1 ai wi·wi·2k +
i = 0, ..., n/2-1 ai wi·wi·2k +  i = 0, ..., n/2-1 – ai+n/2 wi·wi·2k
i = 0, ..., n/2-1 – ai+n/2 wi·wi·2k
=  i = 0, ..., n/2-1 wi·(ai – ai+n/2) wi·2k
i = 0, ..., n/2-1 wi·(ai – ai+n/2) wi·2k
Mit m = n/2 sowie v = w2 gilt wiederum:
yk'' =  i = 0, ..., m-1 wi·(ai – ai+m) vi·k
i = 0, ..., m-1 wi·(ai – ai+m) vi·k
d.h. yk'' ist nichts anderes als die k-te Komponente der Fouriertransformation des Vektors
wi·(ai – ai+m) i = 0, ..., m-1.
Rekursive Ausführung
Durch rekursive Anwendung dieses Verfahrens auf Vektoren jeweils halber Länge wird im Ergebnis die Fouriertransformation berechnet. Bild 2 zeigt schematisch den Ablauf der Berechnung für n = 8.
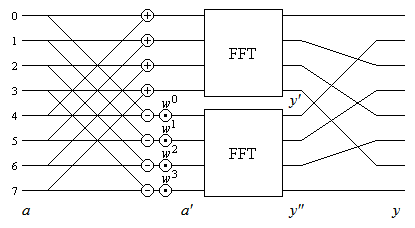
Bild 2: Datenfluss der schnellen Fouriertransformation
Analyse
Um die Fouriertransformation eines Vektors a zu berechnen, ist zunächst ein Vektor a' zu berechnen, dessen Komponenten ai' für i = 0, ..., m-1 wie oben gesehen folgende Werte haben:
ai' = ai + ai+m sowie
ai+m' = wi·(ai – ai+m).
Hierfür sind m Additionen, m Subtraktionen und m Multiplikationen erforderlich sowie nochmals m Multiplikationen, um jeweils wi aus wi-1 zu berechnen. Insgesamt ergibt dies also 2m = n Additionen und 2m = n Multiplikationen.
Anschließend ist rekursiv auf die beiden Hälften von a' die Fouriertransformation anzuwenden.
Die Ergebnisvektoren y' und y'' stellen die geraden und die ungeraden Komponenten von y dar; sie sind noch ineinander zu verschränken (perfect shuffle), um den gewünschten Vektor y zu erhalten. Die Permutation perfect shuffle lässt sich, etwa mit der unten angegebenen Prozedur, in 3/2 n Schritten durchführen.
Die Zeitkomplexität T(n) der FFT ergibt sich somit als
T(n) = 3.5n + 2·T(n/2) sowie
T(1) = 0.
Die Auflösung dieser Rekursion ergibt
T(n) = 3.5n·log(n), d.h.
T(n) ∈ Θ(n log(n)).
Mit der Zeitkomplexität von T(n) ∈ Θ(n log(n)) ist die schnelle Fouriertransformation erheblich schneller als die diskrete Fouriertransformation in Form der Vektor-Matrix-Multiplikation mit der Zeitkomplexität von T(n) ∈ Θ(n2).
Programm
Es folgt eine Implementierung in der Programmiersprache Python.
Die Funktion fft berechnet die Fouriertransformation eines Vektors a, beginnend beim Index lo und der Länge n. Der Parameter w steht für die primitive n-te Einheitswurzel.
Die Funktion eignet sich für die Berechnung der Fouriertransformation sowohl im Körper ℂ der komplexen Zahlen als auch in einem endlichen Körper ℤp. Für Berechnungen im Körper ℤp wird die Python-Klasse ModInt verwendet.
In welchem Zahlentyp gerechnet wird, also complex oder ModInt, wird vom Typ des Parameters w bestimmt,. Die Zahl 1 in dem jeweiligen Zahlentyp wird durch Berechnung von w0 erzeugt.
def fft(a, n, lo, w):
if n>1:
m=n/2
z=w**0 # 1 im jeweiligen Zahlentyp
for i in range(lo, lo+m):
a[i], a[i+m] = a[i]+a[i+m], z*(a[i]-a[i+m])
z*=w
v=w*w
fft(a, m, lo, v)
fft(a, m, lo+m, v)
shuffle_(a, n, lo)
}
Die Funktion shuffle_ verschränkt die beiden, von den rekursiven Aufrufen von fft erzeugten Hälften reißverschlussartig ineinander. Die entsprechende Permutation für n = 8 lautet
| 0 1 2 3 4 5 6 7 |
| 0 4 1 5 2 6 3 7 |
def shuffle_(a, n, lo):
m=n/2
b=a[lo:lo+m]
for i in range(m):
a[lo+2*i]=b[i]
a[lo+2*i+1]=a[lo+m+i]
Mit der folgenden Funktion fftmain wird ein Vektor a der Länge n transformiert.
# w primitive n-te Einheitswurzel
def fftmain(a, w):
fft(a, len(a), 0, w)
Die folgende Funktion complexroot erzeugt eine komplexe primitive n-te Einheitswurzel.
# primitive n-te Einheitswurzel im Koerper der komplexen Zahlen
def complexroot(n):
return complex(cos(2*pi/n), sin(2*pi/n))
Inverse Fouriertransformation
Die inverse Fouriertransformation lässt sich mit demselben Verfahren durchführen. Aufgrund der Definition der inversen Fouriermatrix F -1 wird jedoch statt mit der primitiven n-ten Einheitswurzel w mit der inversen n-ten Einheitswurzel w-1 gearbeitet. In ℂ ist dies die konjugiert komplexe n-te Einheitswurzel w (vgl. o.a. Eigenschaften (5) und (6)). Ferner werden die Elemente der invers zu transformierenden Folge zunächst durch n geteilt.
In der folgenden Implementation werden verschiedene Vorausberechnungen durchgeführt, um die Zahlen 0, 1 und n im jeweiligen Zahlentyp (complex oder ModInt) zu erzeugen.
# w primitive n-te Einheitswurzel
def fftinv(a, w):
n=len(a)
one=w**0 # one = 1 im jeweiligen Zahlentyp, also 1.0 oder ModInt(1)
zero=one-one # zero = 0 im jeweiligen Zahlentyp
n1=zero
for _ in range(n):
n1+=one
# n1 = n im jeweiligen Zahlentyp
for i in range(n):
a[i]/=n1
fftmain(a, one/w)
Anwendungsbeispiel
Das folgende Programm transformiert einen Vektor der Länge 8 von ModInt-Zahlen hin und wieder zurück.
from ModInt import *
ModInt.n=17
a=toModInt([-3,-2,-1,0,1,2,3,4])
for x in a:
print(x, end=" ")
print()
w=ModInt(2) # 2 = Element der Ordnung 8
# Fouriertransformation
fftmain(a, w)
for x in a:
print(x, end=" ")
print()
# inverse Fouriertransformation
fftinv(a, w)
for x in a:
print(x, end=" ")
print()
Zusammenfassung
Die diskrete Fouriertransformation lässt sich interpretieren als Transformation eines Polynoms vom Grad n-1 von der Koeffizientendarstellung in die Stützstellendarstellung. Als Stützstellen werden die n-ten Einheitswurzeln w0, w1, ..., wn-1 verwendet. Im Körper ℂ der komplexen Zahlen sind die Werte
wk = cos(k·2π/n) + i sin(k·2π/n) = eik2π/n mit k ∈ {0, ..., n-1}
die n-ten Einheitswurzeln.
Durch Ausnutzung der Symmetrien der n-ten Einheitswurzeln lässt sich die Fouriertransformation beschleunigen; das Verfahren ist die schnelle Fouriertransformation FFT.
Mit Hilfe der FFT lässt sich die Zeitkomplexität der Polynommultiplikation von Θ(n2) auf Θ(n log(n)) verbessern.
Literatur
[AHU 74] A.V. Aho, J.E. Hopcroft, J.D. Ullman: The Design and Analysis of Computer Algorithms. Addison-Wesley (1974)
[CT 65] J.M. Cooley, J.W. Tukey: An Algorithm for the Machine Calculation of Complex Fourier Series. Math. Comp. 19, 297-301 (1965)
[Sed 88] R. Sedgewick: Algorithms. 2. Auflage, Addison-Wesley (1988)
[Lan 12] H.W. Lang: Algorithmen in Java. 3. Auflage, Oldenbourg (2012)
Den FFT-Algorithmus finden Sie auch in meinem Buch über Algorithmen.
Weitere Themen des Buches: Sortieren, Textsuche, Graphenalgorithmen, Arithmetik, Codierung, Kryptografie, parallele Sortieralgorithmen.
Themen des Buches: Sortieren, Textsuche, Graphenalgorithmen, Arithmetik, Codierung, Kryptografie, parallele Sortieralgorithmen.
1) Die Zahl i ist die imaginäre Einheit i =  -1
-1
2) Da es für n > 2 stets mehrere primitive n-te Einheitswurzeln gibt, ist die Fouriermatrix insofern nicht eindeutig festgelegt.
3) Da die Fouriermatrix symmetrisch ist, lässt sich die Fouriertransformation auch als f(a) = F·a für Spaltenvektoren a definieren.
Weiter mit: [Diskrete Kosinus-Transformation] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 05.03.1997 Updated: 15.06.2025
Diese Webseiten sind größtenteils während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden
