Konvexe Hülle
Konvexe Hülle
Konvexe Polygone
Wir betrachten nun Polygone, also Gebiete, die von einfachen Polygonzügen umschlossen sind.
Definition: Sei p ein Punkt in einem Polygon. Ein Punkt q ist von p aus sichtbar, wenn die Verbindungsstrecke zwischen p und q ganz im Polygon enthalten ist.
Die Vorstellung ist, dass der Rand des Polygons undurchsichtig ist. Ein Punkt ist von einem anderen Punkt aus nicht sichtbar, wenn die Verbindungsstrecke zwischen den Punkten den Rand des Polygons schneidet. In folgendem Bild 1 ist q von p aus nicht sichtbar.
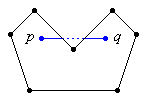
Bild 1: Punkt q ist von p aus nicht sichtbar
Definition: Ein Polygon heißt sternförmig, wenn es einen Punkt enthält, von dem aus alle Punkte des Polygons sichtbar sind. Ein Polygon heißt konvex, wenn von jedem seiner Punkte aus alle Punkte des Polygons sichtbar sind.
Beispiel: Das Polygon von Bild 2a ist konvex; das Polygon von Bild 2b ist sternförmig – alle Punkte sind von der unteren Ecke aus sichtbar.
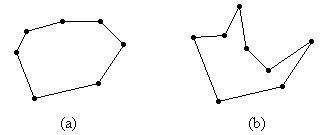
Bild 2: Konvexes Polygon (a), sternförmiges Polygon (b)
Satz: Ein einfacher Polygonzug, der nur konvexe Ecken hat, umschließt ein konvexes Polygon.
Die Umkehrung gilt ebenfalls: wenn die Ecken eines konvexen Polygons entgegen dem Uhrzeigersinn durchlaufen werden, also so, dass die umschlossene Fläche stets links liegt, dann sind alle Ecken konvex.
Konvexe Hülle
Ein konvexes Polygon ist ein Spezialfall einer allgemeinen konvexen Menge von Punkten.
Definition: Eine Menge von Punkten in der Ebene heißt konvex, wenn sie mit je zwei Punkten auch deren Verbindungsstrecke enthält.

Bild 3: Konvexe Menge (a) und nicht konvexe Menge (b)
Definition: Gegeben sei eine Menge M von Punkten in der Ebene. Die konvexe Hülle von M ist die kleinste konvexe Menge, in der M enthalten ist.
Satz: Wenn M eine endliche Menge ist, so ist die konvexe Hülle von M ein konvexes Polygon oder, wenn die Punkte von M alle auf einer Linie liegen, ein Liniensegment.
Beispiel: Bild 4 zeigt eine endliche Menge von Punkten und deren konvexe Hülle.

Bild 4: Menge von Punkten (a) und deren konvexe Hülle (b)
Stellen wir uns die Punkte als Nägel vor, die in einem Brett stecken, dann erhalten wir den Rand der konvexen Hülle, indem wir ein Gummiband um die Nägel spannen.
Problem Konvexe Hülle
Eingabe:
Endliche Menge M von Punkten in der Ebene
Ausgabe:
Diejenigen Punkte von M, die auf dem Rand des konvexen Hüllpolygons von M liegen, in umlaufender Reihenfolge.
Untere Schranke
Es wird gezeigt, dass die Berechnung der konvexen Hülle von n Punkten mindestens so schwer ist wie das Sortieren von n verschiedenen Zahlen.
Hierzu wird das Sortierproblem auf das Problem der Berechnung der konvexen Hülle reduziert. Dies geschieht in drei Schritten:
- Transformation des Sortierproblems in ein Konvexe-Hülle-Problem,
- Lösung des Konvexe-Hülle-Problems,
- Rücktransformation der Lösung des Konvexe-Hülle-Problems in die Lösung des Sortierproblems.
Gegeben sei also ein beliebiges Exemplar des Sortierproblems mit n verschiedenen Zahlen x0, ..., xn-1. Zu jeder dieser Zahlen xi wird der Punkt (xi, xi2) erzeugt.
Die n Punkte liegen auf der Normalparabel (Bild 5), alle sind Eckpunkte des konvexen Hüllpolygons. Das Ergebnis der Berechnung der konvexen Hülle sind die n Eckpunkte in umlaufender Reihenfolge.
Die Lösung des Sortierproblems ergibt sich hieraus, indem zunächst der Eckpunkt mit kleinster x-Koordinate gesucht wird und von diesem aus die x-Koordinaten der anderen Eckpunkte in umlaufender Reihenfolge ausgegeben werden. Die Folge dieser x-Koordinaten ist die sortierte Folge x0, ..., xn-1.
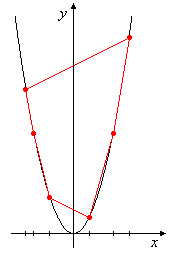
Bild 5: Konvexe Hülle der Punktemenge { (xi, xi2) }
Die Transformation, nämlich das Erzeugen der n Punkte aus den n Zahlen, benötigt Zeit O(n). Die Rücktransformation, nämlich das Suchen des Punktes mit kleinster x-Koordinate, benötigt ebenfalls Zeit O(n). Somit muss die Berechnung der konvexen Hülle Zeit Ω(n log(n)) benötigen. Denn ginge es schneller, so könnten wir schneller als in Zeit Ω(n log(n)) sortieren. Dies aber ist nicht möglich, da Ω(n log(n)) eine untere Schranke für das Sortierproblem ist.
Satz: Die Zeitkomplexität der Berechnung der konvexen Hülle von n Punkten liegt in Ω(n log(n)).
Die im Folgenden vorgestellten Algorithmen mit der Zeitkomplexität von O(n log n) sind also optimal.
Konvexe Hülle eines sternförmigen Polygons
Satz: Die konvexe Hülle eines sternförmigen Polygons mit n Ecken lässt sich in Zeit Θ(n) berechnen.
Beweis: Ein sternförmiges Polygon kann konkave Ecken haben. Die Idee ist, diese konkaven Ecken zu überbrücken, sodass schließlich ein konvexes Polygon entsteht.
Die Ecken des sternförmigen Polygons werden der Reihe nach entgegen dem Uhrzeigersinn durchlaufen. Immer wenn dabei eine konkave Ecke gefunden wird, wird diese überbrückt, sodass sie anschließend im Inneren des Polygons liegt (Bild 6a). Es kann vorkommen, dass die vorherige Ecke, die zunächst konvex war, hierdurch zu einer konkaven Ecke wird (Bild 6b). Es muss also in diesem Fall so weit zurückgegangen werden, bis die jeweils letzte Ecke konvex ist (Bild 6c).
Der Durchlauf beginnt bei einer Ecke mit minimaler y-Koordinate; diese ist auf jeden Fall konvex und braucht nicht untersucht zu werden. Während der Ausführung des Verfahrens bleibt das Polygon immer sternförmig. Zum Schluss hat es nur konvexe Ecken und ist damit konvex.
Obwohl möglicherweise auf dem Weg entlang des Polygonzugs auch zurückgegangen werden muss, benötigt das Verfahren nur O(n) Schritte, denn ein Rückwärtsschritt entsteht nur, wenn zuvor eine Ecke ins Innere des Polygons verbannt wurde. Dies kann höchstens n-mal geschehen.

Bild 6: Überbrücken von konkaven Ecken
Das Verfahren funktioniert im Allgemeinen nur mit sternförmigen Polygonen.1)
Aufgabe 1: Geben Sie einen einfachen, jedoch nicht sternförmigen Polygonzug an, bei dem durch das Verfahren ein nicht einfacher Polygonzug erzeugt wird.
Algorithmen zur Berechnung der konvexen Hülle
Der erste im Folgenden angegebene Algorithmus zur Berechnung der konvexen Hülle einer endlichen Menge von Punkten, der Graham-Scan-Algorithmus, baut auf dem Verfahren für sternförmige Polynome auf.
Es folgen dann zwei weitere Algorithmen, der Jarvis-March-Algorithmus und der Quickhull-Algorithmus.
Literatur
[PSh 85] F.P. Preparata, M.I. Shamos: Computational Geometry. Springer (1985)
[Klei 97] R. Klein: Algorithmische Geometrie. Addison-Wesley (1997)
1) Es gibt jedoch andere Verfahren, die für beliebige einfache Polygonzüge die konvexe Hülle in Zeit Θ(n) berechnen.
Weiter mit: [Graham-Scan-Algorithmus] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 25.12.2002 Updated: 08.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden