Transformationen
Untere Schranke für die Berechnung der konvexen Hülle
Problem
Gegeben ist eine endliche Menge von n Punkten in der Ebene, gesucht ist die konvexe Hülle dieser Punkte. Dies ist der kürzeste konvexe Polygonzug, der diese Punkte umschließt (Bild 1).
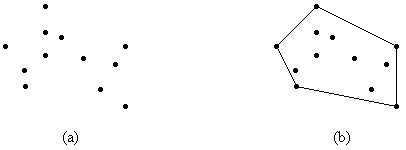
Bild 1: Endliche Menge von Punkten (a) und konvexe Hülle der Punkte (b)
Transformation
Es wird gezeigt, dass die Berechnung der konvexen Hülle von n Punkten mindestens so schwer ist wie das Sortieren von n verschiedenen Zahlen.
Hierzu wird das Sortierproblem auf das Problem der Berechnung der konvexen Hülle reduziert. Dies geschieht in drei Schritten:
- Transformation des Sortierproblems in ein Konvexe-Hülle-Problem,
- Lösung des Konvexe-Hülle-Problems,
- Rücktransformation der Lösung des Konvexe-Hülle-Problems in die Lösung des Sortierproblems.
Bild 2 zeigt schematisch dieses Vorgehen.
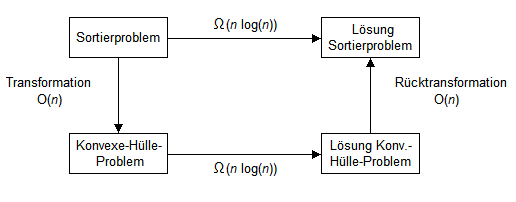
Bild 2: Transformationsschema
Gegeben sei also ein beliebiger Fall des Sortierproblems mit n verschiedenen Zahlen x0, ..., xn-1.
Die Transformation besteht darin, dass zu jeder dieser Zahlen xi der Punkt (xi, xi2) erzeugt wird.
Diese n Punkte liegen auf der Normalparabel (Bild 3). Die konvexe Hülle dieser Punktmenge besteht aus diesen Punkten selber, d.h. alle sind Eckpunkte des konvexen Hüllpolygons. Das Ergebnis der Berechnung der konvexen Hülle sind die n Eckpunkte in umlaufender Reihenfolge.
Aus dieser Lösung des Konvexe-Hülle-Problems ergibt sich die Lösung des Sortierproblems, indem zunächst der Eckpunkt mit kleinster x-Koordinate gesucht wird und von diesem aus die x-Koordinaten der Eckpunkte in umlaufender Reihenfolge ausgegeben werden. Die Folge dieser x-Koordinaten ist die sortierte Folge x0, ..., xn-1.
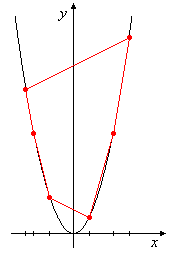
Bild 3: Konvexe Hülle der Punktemenge { (xi, xi2) }
Die Transformation, nämlich das Erzeugen der n Punkte aus den n Zahlen, benötigt Zeit O(n). Die Rücktransformation, nämlich das Suchen des Punktes mit kleinster x-Koordinate, benötigt ebenfalls Zeit O(n). Somit muss die Berechnung der konvexen Hülle Zeit Ω(n log(n)) benötigen. Denn ginge es schneller, so könnten wir schneller als in Zeit Ω(n log(n)) sortieren. Dies aber ist nicht möglich, da Ω(n log(n)) eine untere Schranke für das Sortierproblem ist.
Satz: Die Zeitkomplexität des Problems der Berechnung der konvexen Hülle von n Punkten liegt in Ω(n log(n)).
Algorithmen zur Berechnung der konvexen Hülle mit einer Zeitkomplexität von O(n log n) sind also optimal, so z.B. der Graham-Scan-Algorithmus.
Weiter mit: [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 25.12.2002 Updated: 08.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden