Sortiernetze
Pairwise Sorting Network
Sortiernetze sind spezielle Sortierverfahren, bei denen die Daten durch eine festliegende Folge von Vergleichs-Austausch-Schritten sortiert werden. Neben den Sortiernetzen Odd-even Mergesort, Bitonic Sort und Shellsort ist das hier vorgestellte Pairwise Sorting Network [Par 92] ein weiteres interessantes Sortiernetz mit einer Komplexität von Θ(n·log(n)2) Vergleichern.
Merge-Verfahren
Kernstück des Sortiernetzes ist ein Merge-Verfahren, das aus einer Folge a, deren gerade Teilfolge und deren ungerade Teilfolge jeweils sortiert sind, eine insgesamt sortierte Folge macht. Die gerade Teilfolge von a besteht aus allen ai mit i gerade, also a0, a2, a4 usw. Die ungerade Teilfolge besteht aus allen ai mit i ungerade, also a1, a3, a5 usw. Zusätzliche Voraussetzung ist, dass alle Elemente der geraden Teilfolge kleiner oder gleich den Elementen der ungeraden Teilfolge sind.
Der folgende Algorithmus PairwiseMerge realisiert dieses Merge-Verfahren. Im nächsten Abschnitt ist dessen Funktionsweise anhand des 0-1-Prinzips anschaulich beschrieben.
Algorithmus PairwiseMerge(n)
Eingabe:
Folge a0, ..., an-1 der Länge n > 1, gerade und ungerade Teilfolge sortiert, alle Elemente der geraden Teilfolge kleiner oder gleich den Elementen der ungeraden Teilfolge (n Zweierpotenz)
Ausgabe:
die sortierte Folge
Methode:
- setze d = n/2
- solange d > 1 wiederhole
- setze k = d
- solange k < n wiederhole
- Vergleich [k-d+1 : k]
- setze k = k+2
- setze d = d/2
Korrektheit
Die Korrektheit des Merge-Verfahrens lässt sich mit Hilfe des 0-1-Prinzips zeigen.
Ist n = 2, so ist die Folge nach den angegebenen Voraussetzungen bereits sortiert. Ansonsten wird die 0-1-Folge a = a0, ..., an-1 gedanklich zeilenweise in ein zweispaltiges Feld eingetragen. Die entsprechende Zuordnung der Indexpositionen ist in Bild 1 a gezeigt, hier für n = 16. In den beiden Spalten befinden sich die gerade und die ungerade Teilfolge.
Nach den angegebenen Voraussetzungen sind diese Teilfolgen bereits sortiert, d.h. jede der beiden Spalten beginnt mit einer gewissen Anzahl von Nullen (weiß) und endet mit einer gewissen Anzahl von Einsen (grau). Außerdem sind alle Elemente der linken Spalte kleiner oder gleich den Elemente der rechten Spalte, d.h. in der linken Spalte befinden sich höchstens so viel Einsen wie in der rechten Spalte.
Im Verlauf des Verfahrens PairwiseMerge wird der Unterschied zwischen der Anzahl der Einsen in den beiden Spalten schrittweise jeweils halbiert, bis er höchstens 1 erreicht. Dann aber ist die Folge sortiert. Die durchgeführten Vergleiche lassen sich anschaulich darstellen, indem Blöcke des zweispaltigen Feldes (Bild 1 a) gedanklich nebeneinander angeordnet werden (Bild 1 b-k).
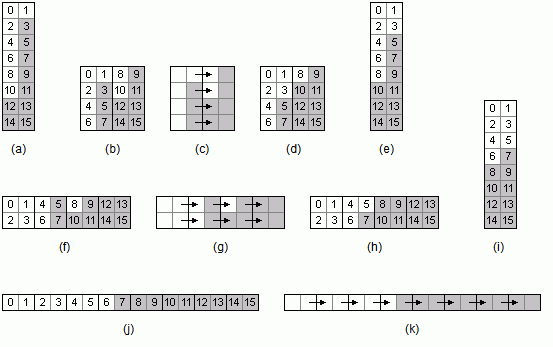
Bild 1: Situationen während der Ausführung von PairwiseMerge
Sortierverfahren
Aus dem Merge-Verfahren lässt sich durch rekursive Anwendung das Sortierverfahren Pairwise Sorting erzeugen.
Algorithmus PairwiseSorting(n)
Eingabe:
Folge a0, ..., an-1 (n Zweierpotenz)
Ausgabe:
die sortierte Folge
Methode:
- wenn n > 1 dann
- Vergleich [i : i+1] für alle i mit i gerade
- PairwiseSorting(n/2) rekursiv auf die gerade und die ungerade Teilfolge anwenden
- PairwiseMerge(n)
Bild 2 zeigt das Pairwise-Sorting-Sortiernetz für n = 16.
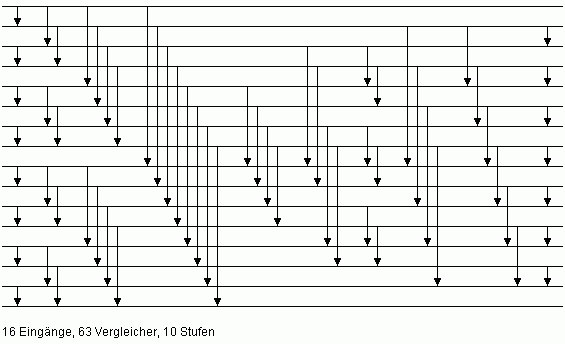
Bild 2: Pairwise Sorting Network für n = 16
Zusammenfassung
Das Sortiernetz Pairwise Sorting benötigt O(n log(n)2) Vergleicher; es hat damit dieselbe asymptotische Komplexität wie die Sortiernetze Odd-even Mergesort, Bitonic Sort und Shellsort. Tatsächlich umfasst es exakt genauso viele Vergleicher wie Odd-even Mergesort.
Literatur
[Bat 68] K.E. Batcher: Sorting Networks and their Applications. Proc. AFIPS Spring Joint Comput. Conf., Vol. 32, 307-314 (1968)
[Par 92] I. Parberry: The pairwise sorting network. Parallel Processing Letters, 2, 205-2011 (1992)
Weiter mit: [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 23.02.2015 Updated: 07.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden