Sortierverfahren
Shellsort
Shellsort ist eines der am längsten bekannten Sortierverfahren (benannt nach seinem Urheber D.L. Shell [She 59]). Es ist sehr schnell, einfach zu verstehen und einfach zu implementieren, allerdings ist seine Analyse etwas aufwendiger.
Idee
Die Idee des Verfahrens ist, die Daten als zweidimensionales Feld anzuordnen und spaltenweise zu sortieren. Dadurch wird eine Grobsortierung bewirkt. Dann werden die Daten als schmaleres zweidimensionales Feld angeordnet und wiederum spaltenweise sortiert. Dann wird das Feld wiederum schmaler gemacht usw. Zum Schluss besteht das Feld nur noch aus einer Spalte.
Werden die Feldbreiten geschickt gewählt, reichen jedes Mal wenige Sortierschritte aus, um die Daten spaltenweise zu sortieren bzw. am Ende, wenn nur noch eine Spalte vorhanden ist, vollständig zu sortieren. Die Effizienz von Shellsort hängt von der Folge der gewählten Feldbreiten ab.
Beispiel: Sei 3 7 9 0 5 1 6 8 4 2 0 6 1 5 7 3 4 9 8 2 die zu sortierende Datenfolge. Als erstes werden die Daten als Feld mit 7 Spalten angeordnet (links), anschließend werden die Spalten sortiert (rechts):
|
|
|
Die Datenfolge lautet jetzt 3 3 2 0 5 1 5 7 4 4 0 6 1 6 8 7 9 9 8 2; die Elemente 8 und 9 sind schon ziemlich an das Ende der Datenfolge gelangt; allerdings steht auch noch ein sehr kleines Element (die 2) dort. Im nächsten Schritt werden die Daten in 3 Spalten angeordnet, die wiederum sortiert werden:
|
|
|
Jetzt sind die Daten bereits fast vollständig sortiert, die Datenfolge lautet 0 0 1 1 2 2 3 3 4 4 5 6 5 6 8 7 7 9 8 9. Wenn die Daten anschließend in einer Spalte angeordnet werden, müssen lediglich noch eine 6, eine 8 und eine 9 etwas weiter nach unten sortiert werden.
Implementierung
Tatsächlich werden die Daten nicht in unterschiedlich breite Felder umarrangiert, sondern die Daten stehen in einem eindimensionalen Feld, das entsprechend indiziert wird. Beispielsweise bilden die Elemente an den Indexpositionen 0, 5, 10, 15 usw. die erste Spalte eines 5-spaltigen Feldes. Die durch die jeweilige Indizierung entstehenden "Spalten" werden im Shellsort-Algorithmus mittels Insertionsort sortiert, da Insertionsort bei teilweise vorsortierten Daten recht effizient ist.
Die folgende Funktion shellsort sortiert ein Array a beginnend beim Index 0 bis zum Index n-1. Die Anzahl der Spalten, in die die Daten jeweils arrangiert werden, ist im Array cols angegeben. Zuerst werden die Daten also in 1391376 Spalten angeordnet (sofern so viele Daten vorhanden sind), zum Schluss in einer Spalte. Diese im Array cols befindlichen Werte sind entscheidend für die Zeitkomplexität von Shellsort – es dürfen nicht zu viele Werte sein, damit nicht zu viele Iterationen zustande kommen, und die Werte müssen sorgfältig aufeinander abgestimmt sein, damit pro Iteration möglichst wenig Sortierschritte erforderlich sind. Eine entsprechende Analyse folgt im Anschluss an den Algorithmus. Die hier verwendeten Werte stammen von Sedgewick [Sed 96].
Jede Spalte wird mit Insertionsort sortiert. Zuerst werden die Daten der zweiten Zeile (diese beginnt bei i = h) in ihren jeweiligen Spalten einsortiert, dann die Daten der dritten Zeile (wenn i den Wert 2h erreicht) usw.
Die Sortierfunktion ist in der Klasse ShellSorter gekapselt. Die Methode sort übergibt das zu sortierende Array an das Array a, setzt n auf dessen Länge und ruft shellsort auf.
Mit den Anweisungen
s.sort(b);
wird ein Objekt vom Typ ShellSorter angelegt und anschließend die Methode sort zum Sortieren eines Arrays b aufgerufen. Es folgt das Programm.
{
private int[] a;
private int n;
public void sort(int[] a)
{
this.a=a;
n=a.length;
shellsort();
}
private void shellsort()
{
int[] cols = {1391376, 463792, 198768, 86961, 33936,
13776, 4592, 1968, 861, 336, 112, 48, 21, 7, 3, 1};
for (int k=0; k<cols.length; k++)
{
int h=cols[k];
for (int i=h; i<n; i++)
{
int j=i;
int t=a[j];
while (j>=h && a[j-h]>t)
{
a[j]=a[j-h];
j=j-h;
}
a[j]=t;
}
}
}
}
Analyse
Die Korrektheit des Verfahrens ist gesichert, da im letzten Schritt (mit h = 1) ein normales Insertionsort auf der gesamten Folge durchgeführt wird. Durch die vorherigen Schritte (h = 3, 7, 21, ...) sind die Daten jedoch bereits so vorsortiert, dass wenige Insertionsort-Schritte ausreichen. Wie viele genau, ist Gegenstand der folgenden eingehenden Analyse. Ausschlaggebende Bedeutung hat hierbei die Folge der Feldbreiten (im Folgenden als h-Folge bezeichnet).
Grundlagen
Ein Brief kostet 16F Porto, eine Postkarte 11F. Es sind nur Briefmarken zu 3F und zu 7F vorhanden. Ist es möglich, den Brief bzw. die Postkarte exakt zu frankieren?
Offenbar besteht das Problem darin, die Zahlen 16 bzw. 11 jeweils als Linearkombination k·3 + l·7 mit ganzzahligen, nichtnegativen Koeffizienten k, l darzustellen. Welche natürlichen Zahlen lassen sich aus Vielfachen von 3 und 7 kombinieren und welche nicht?
Definition: Seien g, h ∈ ℕ. Wir nennen eine Zahl f eine Kombination von g und h, wenn sich f als Linearkombination f = kg + lh mit Koeffizienten k, l ∈ ℕ0 darstellen lässt.
Beispiel: Es gilt 16 = 3·3 + 1·7, damit ist 16 eine Kombination von 3 und 7. Der Brief kann also exakt frankiert werden.
Wie aber steht es um die Postkarte? Kann auch die Postkarte exakt frankiert werden?
Definition: Seien g, h ∈ ℕ teilerfremd. Wir bezeichnen mit N(g, h) die (endliche) Menge der natürlichen Zahlen, die keine Kombinationen von g und h sind und mit γ(g, h) die größte dieser Zahlen:
N(g, h) = { f ∈ ℕ | ¬ ∃ k, l ∈ ℕ0 : f = kg + lh },
γ(g, h) = max(N(g, h)).
Beispiel: Seien g = 3, h = 7. Dann ist
N(g, h) = {1, 2, 4, 5, 8, 11} und
γ(g, h) = 11.
Die Postkarte kann also nicht exakt frankiert werden.
Satz: Sind g, h ∈ ℕ teilerfremd, so gilt:
γ(g, h) = (g-1)·(h-1) – 1,
d.h. jede natürliche Zahl f mit f ≥ (g-1)·(h-1) ist eine Kombination von g und h.
h-Sortierung
Definition: Sei h ∈ ℕ. Eine Folge a0, ..., an-1 heißt h-sortiert, wenn für alle i ∈ {0, ..., n-1-h} gilt
ai ≤ ai+h.
Eine h-sortierte Folge entsteht, wenn die Folge zeilenweise in ein Feld mit h Spalten geschrieben wird und die Spalten sortiert werden. Eine 1-sortierte Folge ist sortiert.
Satz: Seien g, h ∈ ℕ. Eine g-sortierte Folge bleibt g-sortiert, wenn sie h-sortiert wird.
Beweis: → Beweis
Definition: Eine Folge, die g-sortiert und h-sortiert ist, nennen wir g,h-sortiert.
Satz: Eine g,h-sortierte Folge ist g+h-sortiert.
Beweis: Sei a = a0, ..., an-1 die g,h-sortierte Folge. Es ist zu zeigen, dass für alle i ∈ {0, ..., n-1-(g+h)} gilt:
ai ≤ ai+g+h.
Dies ist aber der Fall, denn ai ≤ ai+g, weil die Folge g-sortiert ist und ai+g ≤ ai+g+h, weil die Folge h-sortiert ist.
Hieraus folgt sofort der folgende Satz.
Satz: Ist eine Folge g,h-sortiert, dann ist sie (kg+lh)-sortiert für alle k, l ∈ ℕ0, d.h. die Folge ist f-sortiert für alle f, die Kombinationen von g und h sind.
Satz: Sei a eine g,h-sortierte Folge, wobei g und h teilerfremd sind. Für beliebige Elemente ai und aj, die einen Abstand j – i von mindestens (g-1)·(h-1) haben, gilt:
ai ≤ aj.
Beweis: Sei f = j – i. Ist f ≥ (g-1)·(h-1), so ist f Kombination von g und h, damit ist die Folge f-sortiert, also gilt
ai ≤ ai+f = aj.
Der Satz besagt also, dass in einer g,h-sortierten Folge, wobei g und h teilerfremd sind, rechts von jedem Element ai kleinere Elemente nur innerhalb der nächsten (g-1)·(h-1) – 1 Positionen vorkommen können; die darauf folgenden Elemente sind alle größer oder gleich ai.
Behauptung: Sei a = a0, ..., an-1 eine g,h-sortierte Folge, wobei g und h teilerfremd sind, sei ferner d eine Variable. Liegen sowohl g als auch h in O(d), so genügen O(n·d) Sortierschritte, um die Folge d-sortiert zu machen.
Beweis: Nach Aussage des vorigen Satzes befinden sich rechts von jedem Element ai kleinere Elemente nur innerhalb der nächsten (g-1)·(h-1) – 1 Positionen.
Wird die Folge jetzt d-sortiert, so kommt in der Spalte unter ai nur jedes d-te dieser maximal (g-1)·(h-1) – 1 kleineren Elemente vor. Unter jedem ai (i = 0, ..., n-1) stehen also maximal (g-1)·(h-1)/d kleinere Elemente, mit denen ai vertauscht werden muss. Somit werden maximal n·(g-1)·(h-1)/d Schritte für die d-Sortierung benötigt.
Da sowohl g als auch h in O(d) liegen, sind dies O(n·d) Schritte.
Hieraus lassen sich obere Schranken für die Anzahl der Sortierschritte von Shellsort gewinnen.
Obere Schranken
Satz: Mit der h-Folge 1, 3, 7, 15, 31, 63, 127, ..., 2k – 1, ... benötigt Shellsort O(n·
n) Schritte, um eine Datenfolge der Länge n zu sortieren (Papernov und Stasevic [PS 65]).
Beweis: Sei ht dasjenige Element der h-Folge, das am nächsten bei n liegt. Wir analysieren das Verhalten von Shellsort getrennt für die Elemente hk mit k ≤ t und für die Elemente hk mit k > t.
Sei k ≤ t. Da hk = 2k – 1 ist, sind hk+1 und hk+2 teilerfremd und liegen in O(hk). Daher genügen O(n·hk) Sortierschritte, um die Datenfolge hk-sortiert zu machen.
Da die hk eine geometrische Reihe bilden, liegt die Summe aller hk mit k = 1, ..., t in O(ht) = O(n). Damit werden insgesamt O(n·n) Sortierschritte für diesen Teil des Algorithmus benötigt.
Sei nun k > t. Wenn die Daten in einem Feld mit hk Spalten arrangiert werden, enthält jede Spalte n/hk Elemente. Es werden daher O((n/hk)2) Sortierschritte pro Spalte benötigt, da Insertionsort quadratische Komplexität hat. Es gibt hk Spalten, dies führt insgesamt zu O((n/hk)2·hk) = O(n·n/hk) Sortierschritten für die hk-Sortierung der gesamten Datenfolge.
Wiederum bilden die n/hk eine geometrische Reihe, deren Summe in O(n/ht) = O(n) liegt. Somit sind für k > t ebenfalls O(n·n) Sortierschritte erforderlich, sodass sich insgesamt die obere Schranke von O(n·n) ergibt.
Es kann gezeigt werden, dass mit dieser Folge die obere Schranke im schlechtesten Fall auch erreicht wird. Es gibt aber andere h-Folgen, die zu einem effizienteren Verhalten von Shellsort führen.
Satz: Mit der h-Folge 1, 2, 3, 4, 6, 8, 9, 12, 16, ..., 2p3q, ... benötigt Shellsort O(n·log(n)2) Schritte, um eine Datenfolge der Länge n zu sortieren (Pratt [Pra 79]).
Beweis: Ist g = 2 und h = 3, so ist γ(g, h) = (g-1)·(h-1) – 1 = 1, d.h. in einer 2,3-sortierte Folge kann jedes Element höchstens ein kleineres Element unmittelbar rechts von sich stehen haben. Es genügen daher n Sortierschritte, um die Datenfolge zu sortieren.
Betrachtet man Elemente mit geradem und mit ungeradem Index getrennt, so wird klar, dass ebenfalls n Sortierschritte genügen, um eine 4,6-sortierte Folge 2-sortiert zu machen. Analog dazu genügen n Sortierschritte, um eine 6,9-sortierte Folge 3-sortiert zu machen.
Die obige h-Folge ist so konstruiert, dass zu jedem hk auch 2hk und 3hk vorkommen. Insgesamt sind dies log(n)2 Elemente; für jedes hk genügen n Sortierschritte, somit ergibt sich eine Komplexität von O(n log(n)2).
Die h-Folge von Pratt liefert zwar asymptotisch das beste Ergebnis, sie besteht jedoch aus relativ vielen, nämlich log(n)2 Elementen. Insbesondere bei Daten, die bereits vorsortiert sind, sind h-Folgen mit weniger Elementen besser, da die Daten ja pro Element einmal durchlaufen werden müssen, auch wenn nur wenige Sortierschritte ausgeführt werden.
Durch Kombination der Argumente aus diesen beiden Sätzen lassen sich h-Folgen mit O(log(n)) Elementen gewinnen, die in der Praxis zu sehr guten Ergebnissen führen, so etwa die h-Folge von Sedgewick aus dem angegebenen Programm [Sed 96]. Allerdings scheint es keine h-Folge zu geben, mit der Shellsort eine Komplexität von O(n log(n)) erreicht (siehe [Sed 96]). Möglicherweise gibt es jedoch h-Folgen, mit der diese Komplexität im Durchschnitt erreichbar ist.
Sortiernetz
Durch Verwendung von Bubblesort anstelle des datenabhängigen Insertionsort lässt sich Shellsort auch als Sortiernetz implementieren. Mit der h-Folge 2p3q besteht es aus Θ(n·log(n)2) Vergleichern. Das folgende Bild 1 zeigt ein entsprechendes Sortiernetz für n = 8.
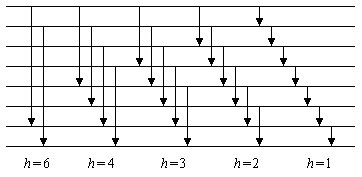
Bild 1: Shellsort-Sortiernetz für n = 8
Strukturierte Implementierung
Das Programm lässt sich noch besser strukturieren, indem das Einsortieren eines Elements t in eine Funktion insert ausgelagert wird. Diese Funktion insert ist in ähnlicher Weise programmiert wie die Funktion insert beim Sortierverfahren Insertionsort.
Die Anweisung a[i]=a[i-=h]; ist gleichbedeutend mit der Anweisungsfolge a[i]=a[i-h]; i=i-h;.
In der Funktion shellsort wird eine For-Each-Schleife verwendet, um alle Elemente des Arrays cols der Reihe nach durchzugehen. 1)
{
while (i>=h && a[i-h]>t)
a[i]=a[i-=h];
a[i]=t;
}
private void shellsort()
{
int[] cols = {1391376, 463792, 198768, 86961, 33936,
13776, 4592, 1968, 861, 336, 112, 48, 21, 7, 3, 1};
for (int h : cols)
for (int i=h; i<n; i++)
insert(a[i], i, h);
}
Literatur
[Knu 73] D.E. Knuth: The Art of Computer Programming, Vol. 3 - Sorting and Searching. Addison-Wesley (1973)
[Pra 79] V. Pratt: Shellsort and Sorting Networks. Garland, New York (1979)
[PS 65] A. Papernov, G. Stasevic: A Method of Information Sorting in Computer Memories. Problems of Information Transmission 1, 63-75 (1965)
[Sed 88] R. Sedgewick: Algorithms. 2. Auflage, Addison-Wesley (1988)
[Sed 96] R. Sedgewick: Analysis of Shellsort and Related Algorithms. In: Josep Díaz, Maria Serna (Eds.): Algorithms - ESA '96, Fourth Annual European Symposium, Barcelona, Lecture Notes in Computer Science, Vol. 1136, Springer, 1-11 (1996)
[She 59] D.L. Shell: A High-Speed Sorting Procedure. Communications of the ACM, 2, 7, 30-32 (1959)
[Lan 12] H.W. Lang: Algorithmen in Java. 3. Auflage, Oldenbourg (2012)
Shellsort und andere Sortierverfahren, so etwa Quicksort, Heapsort und Mergesort, finden Sie auch in meinem Buch über Algorithmen.
Weitere
Themen des Buches: Textsuche, Graphenalgorithmen, algorithmische Geometrie, Arithmetik, Codierung, Kryptografie, parallele Sortieralgorithmen.
1) In Java durchläuft die For-Each-Schleife ein Array in der Reihenfolge der Indexpositionen – dies ist wichtig bei Shellsort, denn die Reihenfolge der h-Werte ist wesentlich für die Korrektheit des Verfahrens.
Weiter mit: [Untere Schranken für das Sortieren] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 29.01.1998 Updated: 05.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden