Sortierverfahren

Mergesort

Das Sortier­verfahren Mergesort erzeugt eine sortierte Folge durch Verschmelzen (engl.: to merge) sortierter Teilstücke.1) Mit einer Zeit­komplexität von Θ(n log(n)) ist das Verfahren optimal.

Idee

Ähnlich wie Quicksort beruht das Verfahren auf dem Divide-and-Conquer-Prinzip (teile und herrsche)Erklärung. Die zu sortierende Folge wird zunächst in zwei Hälften aufgeteilt (divide), die jeweils für sich sortiert werden (conquer). Dann werden die sortierten Hälften zu einer insgesamt sortierten Folge verschmolzen (combine) (Bild 1).

 

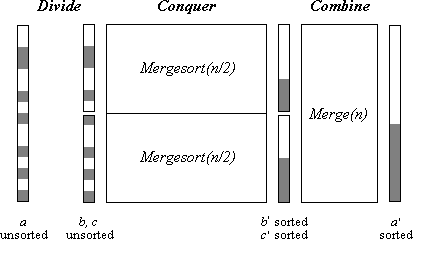
Bild 1: Mergesort(n) 

Bild 1: Mergesort(n)

 

Die folgende Funktion mergesort sortiert eine Folge a vom unteren Index lo bis zum oberen Index hi.

void mergesort(int lo, int hi)
{
    if (lo<hi)
    {
        int m=lo+(hi-lo)/2;
        mergesort(lo, m);
        mergesort(m+1, hi);
        merge(lo, m, hi);
    }
}

Zunächst wird geprüft, ob die Folge aus mehr als einem Element besteht. Dies ist der Fall, wenn lo kleiner als hi ist. In diesem Fall wird als erstes die Mitte m zwischen lo und hi bestimmt2). Anschließend wird die untere Hälfte der Folge (von lo bis m) sortiert und dann die obere Hälfte (von m+1 bis hi), und zwar durch rekursiven Aufruf von mergesort. Danach werden die sortierten Hälften durch Aufruf der Prozedur merge verschmolzen.

Die Funktionen mergesort und merge sind in eine Klasse MergeSorter eingebettet, in der das Datenarray a sowie ein benötigtes Hilfsarray b deklariert sind.

Die Hauptarbeit des Mergesort-Algorithmus liegt im Verschmelzen der sortierten Teilstücke, also in der Funktion merge. Es gibt unter­schiedliche Ansätze für die Implementierung dieser Funktion.

a) Einfache Variante der Funktion merge

Diese Implementation der Funktion merge kopiert zunächst die beiden sortierten Hälften der Folge a hinter­einander in eine neues Array b. Dann vergleicht sie die beiden Hälften mit einem Index i und einem Index j elementweise und kopiert jeweils das nächstgrößte Element zurück nach a (Bild 2).

 

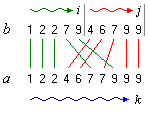
Bild 2: Verschmelzen zweier sortierter Hälften 

Bild 2: Verschmelzen zweier sortierter Hälften

 

Es kommt dabei am Ende zu der Situation, dass der eine Index am Ende seiner Hälfte angekommen ist, der andere Index aber noch nicht. Dann muss im Prinzip noch der Rest der entsprechenden Hälfte zurück­kopiert werden. Tatsächlich ist dies aber nur bei der vorderen Hälfte erforderlich. Bei der hinteren Hälfte stehen die betreffenden Elemente schon an Ort und Stelle (vgl. folgende Simulation).

Folgende Funktion merge ist eine mögliche Implementierung dieses Ansatzes.

// einfache Merge-Variante a
void merge(int lo, int m, int hi)
{
    int i, j, k;

    // beide Hälften von a in Hilfsarray b kopieren
    for (i=lo; i<=hi; i++)
        b[i]=a[i];

    i=lo; j=m+1; k=lo;
    // jeweils das nächstgrößte Element zurückkopieren
    while (i<=m && j<=hi)
        if (b[i]<=b[j])
            a[k++]=b[i++];
        else
            a[k++]=b[j++];

    // Rest der vorderen Hälfte falls vorhanden zurückkopieren
    while (i<=m)
        a[k++]=b[i++];
}

In Java ist die Kurz­schreib­weise k++ gleich­bedeutend mit k=k+1 und die Anweisung a[k++]=b[i++]; ist äquivalent zu der Anweisungs­folge a[k]=b[i]; k=k+1; i=i+1;.

b) Effizientere Variante der Funktion merge

Tatsächlich genügt es, nur die vordere Hälfte der Folge in ein neues Array b auszulagern. Die hintere Hälfte bleibt an Ort und Stelle im Array a. Dadurch wird nur halb soviel zusätzlicher Speicher­platz und nur halb soviel Zeit zum Kopieren benötigt [Som 04].

Beim Zurück­kopieren wird indirekt überwacht, ob die Elemente des Arrays b schon fertig zurück­kopiert sind; dies ist der Fall, wenn der Index k den Index j erreicht. Ähnlich wie in Variante a befindet sich ein dann möglicher­weise noch ver­bleibender Rest der hinteren Hälfte bereits an Ort und Stelle (vgl. folgende Simulation).

Dieser Ansatz ist in folgender Implementation der Funktion merge verwirklicht.

// effizientere Merge-Variante b
void merge(int lo, int m, int hi)
{
    int i, j, k;

    i=0; j=lo;
    // vordere Hälfte von a in Hilfsarray b kopieren
    while (j<=m)
        b[i++]=a[j++];

    i=0; k=lo;
    // jeweils das nächstgrößte Element zurückkopieren
    while (k<j && j<=hi)
        if (b[i]<=a[j])
            a[k++]=b[i++];
        else
            a[k++]=a[j++];

    // Rest von b falls vorhanden zurückkopieren
    while (k<j)
        a[k++]=b[i++];
}

c) Bitonische Variante der Funktion merge

Bei dieser Variante der Funktion merge wird die vordere Hälfte der Folge in ihrer normalen Reihenfolge, die hintere Hälfte jedoch in umgekehrter Reihenfolge in das Array b kopiert [Sed 88]. Dadurch entsteht eine zunächst ansteigende und dann abfallende Folge (eine sogenannte bitonische Folge).

Die Funktion merge durchläuft nun mit dem Index i die vordere Hälfte von links nach rechts und mit dem Index j die hintere Hälfte von rechts nach links. Das jeweils nächstgrößte Folgen­element wird in das Array a zurück­kopiert. Die gesamte Folge ist fertig zurück­kopiert, wenn i und j sich überkreuzen, d.h. wenn i > j wird (Bild 3). Es ist dabei nicht notwendig, dass i und j in "ihren" Hälften bleiben.

 

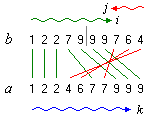
Bild 3: Verschmelzen zweier gegenläufig sortierter Hälften 

Bild 3: Verschmelzen zweier gegenläufig sortierter Hälften

 

Die folgende Version der Funktion merge realisiert diesen Ansatz.

// bitonische Merge-Variante c
void merge(int lo, int m, int hi)
{
    int i=lo, j=hi, k=lo;

    // vordere Hälfte in Array b kopieren
    while (i<=m)
        b[k++]=a[i++];

    // hintere Hälfte in umgekehrter Reihenfolge in Array b kopieren
    while (j>m)
        b[k++]=a[j--];

    i=lo; j=hi; k=lo;
    // jeweils das nächstgrößte Element zurückkopieren,
    // bis i und j sich überkreuzen
    while (i<=j)
        if (b[i]<=b[j])
            a[k++]=b[i++];
        else
            a[k++]=b[j--];
}

Diese Variante von merge benötigt unabhängig davon, ob die Eingabedaten sortiert, umgekehrt sortiert oder zufällig vorliegen, immer genau gleich viele Schritte.

Im Gegensatz zu den beiden anderen Varianten ist es hier möglich, dass die ursprüng­liche Reihenfolge gleich großer Elemente der Folge verändert wird (das Sortier­verfahren ist nicht stabil).3)

Programm

Die folgende Klasse MergeSorter kapselt die Funktionen mergesort und merge. Die Methode sort übergibt das zu sortierende Array an das Array a, legt das Hilfsarray b an und ruft mergesort auf.

Mit den Anweisungen

MergeSorter s=new MergeSorter();
s.sort(c);

wird ein Objekt vom Typ MergeSorter angelegt und anschließend die Methode sort zum Sortieren eines Arrays c aufgerufen.

Es folgt das Programm. Das Hilfsarray b muss je nach der gewählten Implementation der Funktion merge dimensioniert werden, und zwar mit (n+1)/2 Einträgen in Variante b und mit n Einträgen in den Varianten a und c.

 

public class MergeSorter
{
    private int[] a;
    private int[] b;    // Hilfsarray
    private int n;

    public void sort(int[] a)
    {
        this.a=a;
        n=a.length;
        // je nach Variante entweder/oder:
        b=new int[(n+1)/2];    b=new int[n];
        mergesort(0, n-1);
    }

    private void mergesort(int lo, int hi)
    {
        if (lo<hi)
        {
            int m=lo+(hi-lo)/2;
            mergesort(lo, m);
            mergesort(m+1, hi);
            merge(lo, m, hi);
        }
    }

    private void merge(int lo, int m, int hi)
    {
        // hier eine der oben angegebenen Implementationen einfügen
    }

}    // end class MergeSorter

Analyse

Die Funktion merge benötigt in der einfachen Implementation höchstens 2n Schritte (n Schritte zum Kopieren der Folge in das Hilfsarray b und höchstens weitere n Schritte zum Zurück­kopieren von b in a. Die Zeit­komplexität des Mergesort-Verfahrens beträgt also

T(n) ≤ 2n + 2 T(n/2)   und

T(1)  =  0.

Die Auf­lösung dieser Rekursions­gleichung ergibt

T(n) ≤ 2n log(n)  ∈  O(n log(n)).

Das Verfahren ist somit optimal, da die untere Schranke für das Sortier­problem von Ω(n log(n)) erreicht wird.

In der Implementation nach Variante b benötigt die Funktion merge lediglich höchstens 1.5n Schritte (n/2 Schritte zum Kopieren der vorderen Hälfte der Folge in das Array b, nochmals n/2 Schritte zum Zurück­kopieren von b in a, und maximal weitere n/2 Schritte zum Durchlaufen der hinteren Hälfte der Folge). Dadurch verringert sich die Zeit­komplexität des Mergesort-Verfahrens auf höchstens 1.5n log(n) Schritte.

Zusammenfassung

Das Sortier­verfahren Mergesort hat eine Zeit­komplexität von Θ(n log(n)) und ist damit optimal. Anders als das ebenfalls optimale Heapsort benötigt Mergesort zusätzlichen Speicher­platz der Größe Θ(n) für das Hilfsarray.

Die Funktion merge lässt sich auf verschiedene Weisen implementieren. Die Variante b ist die effizienteste der hier dar­gestellten Möglich­keiten, sowohl hinsichtlich der Laufzeit als auch hinsichtlich des benötigten Speicher­platzes.

Das explizite Auslagern von Daten­elementen in das Hilfsarray lässt sich vermeiden, indem im voraus­gehenden Rekursions­schritt das Hilfsarray zum Zielarray der Methode merge gemacht wird. Hierdurch sinkt die Zeit­komplexität auf 1.0n log(n) Schritte gegenüber 1.5n log(n) Schritten in Variante b. Für diese Variante f von Mergesort gibt es eine recht elegante Implementierung in C++.

Neben der rekursiven Version von Mergesort gibt es auch eine iterative Version. In der iterativen Version werden bottom-up durch Ausführung der Funktion merge zunächst die Teilstücke der Länge 2 sortiert, dann die Teilstücke der Länge 4, dann der Länge 8 usw.

Eine Variante von Mergesort, die nach dem iterativen Prinzip arbeitet und dabei bestehende Vor­sortierungen in den Eingabedaten ausnutzt, ist Natural Mergesort. Natural Mergesort ist in manchen günstigen Fällen besonders effizient, insbesondere wenn die bitonische merge-Variante benutzt wird.

Literatur

[Knu 73]   D.E. Knuth: The Art of Computer Programming, Vol. 3 - Sorting and Searching. Addison-Wesley (1973)

[HS 81]   E. Horowitz, S. Sahni: Algorithmen. Springer (1981)

[Sed 88]   R. Sedgewick: Algorithms. 2. Auflage, Addison-Wesley (1988)

[Som 04]   P. Sommerlad: (Persönliche Korrespondenz). Peter Sommerlad, Hochschule für Technik Rapperswil, Schweiz (2004)

[OW 90]   T. Ottmann, P. Widmayer: Algorithmen und Datenstrukturen. BI-Wissenschaftsverlag (1990)

[Lan 12]   H.W. Lang: Algorithmen in Java. 3. Auflage, Oldenbourg (2012)

Mergesort und andere Sortierverfahren, so etwa Quicksort, Heapsort und Shellsort, finden Sie auch in meinem Buch über Algorithmen.
Weitere(vertikaler Abstand) Themen des Buches: Textsuche, Graphenalgorithmen, Arithmetik, Codierung, Kryptografie, parallele Sortieralgorithmen.

Buch

[Weitere Informationen]

1)  Statt verschmelzen wird in der deutschen Literatur auch das Wort mischen verwendet. Aber mischen bedeutet eher durch­einander bringen, also genau das Gegenteil von sortieren.

2)  Die Berechnung lo+(hi-lo)/2 anstelle der einfacheren Berechnung (lo+hi)/2 wird wegen der Gefahr eines Integer-Überlaufs gewählt, der entsteht, wenn lo+hi größer als 2.147.483.647 wird.

3)  Der Begriff nicht stabil im Zusammenhang mit Sortier­verfahren bedeutet nicht, dass das Programm gelegentlich abstürzt, sondern dass die ursprüng­liche Reihenfolge von gleich großen Elementen möglicher­weise verändert wird.
Stabilität ist wichtig beim Sortieren von Datensätzen. Wird etwa eine alphabetisch sortierte Mitglieder­liste eines Vereins nach den Eintritts­jahren der Mitglieder sortiert, so sollen möglichst die Mitglieder ein und desselben Eintritts­jahres alphabetisch sortiert bleiben. Dies wird erreicht, wenn ein stabiles Sortier­verfahren angewendet wird.

 

Weiter mit:   [Natural Mergesort]   [Mergesort iterativ]   [Shellsort]   oder   [up]

 

H.W. Lang   mail@hwlang.de   Impressum   Datenschutz
Created: 19.01.2000   Updated: 05.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden