Mathematische Grundlagen

Norm

Definition

Definition:  Sei V ein Vektorraum über ℝ. Eine Abbildung  ||  || : V → ℝ  heißt Norm, wenn für alle x, y ∈ V und c ∈ ℝ folgendes gilt:

||x||  =  0  ⇔  x = 0

||c·x||  =  |c| · ||x||

||x + y|| ≤ ||x|| + ||y||

Hierbei ist |c| der Betrag der reellen Zahl c.

Aus den drei Bedingungen folgt ||x|| ≥ 0 für alle x ∈ V (siehe Aufgabe 2).

Anschaulich ist die Norm eines Vektors so etwas wie die Länge des Vektors.

Beispiel:  Sei V der Vektorraum ℝ2 über ℝ. Dann ist

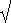||x||   =   Wurzelx02 + x12

für alle x = (x0, x1) ∈ ℝ2 eine Norm in ℝ2, die euklidische Norm.

In der geo­metrischen Inter­pretation ist ||x|| die Länge des Ortsvektors zum Punkt (x0, x1) in der Ebene.

p-Norm

Die euklidische Norm lässt sich verall­gemeinern zur p-Norm.

Definition:  Sei p ∈ ℝ mit p ≥ 1. Dann ist

||x||p  =  (|x0|p + |x1|p)1/p

für alle x = (x0, x1) ∈ ℝ2 eine Norm in ℝ2.

 

Für p = 2 ergibt sich gerade die euklidische Norm.

 

Für p = 1 ergibt sich die Betrags­summen­norm

||x||1  =  |x0| + |x1|

 

Für p → ∞ ergibt sich die Maximumsnorm

||x||∞  =  max(|x0|, |x1|)

 

Die p-Norm lässt sich allgemein für den ℝn definieren:

Definition:  Sei p ∈ ℝ mit p ≥ 1. Dann ist

||x||p  =  ( Summei=0, ..., n-1  |xi|p )1/p

für alle x = (x0, ..., xn-1) ∈ ℝn eine Norm in ℝn.

 

Ein Vektorraum V, in dem eine Norm definiert ist, heißt normierter Raum.

Beliebige Vektorräume

Sei K eine Körper und V ein Vektorraum über K. Damit man in V eine Norm definieren kann, ist es erforderlich, dass es in K eine Betrags­funktion gibt.

Definition:  Sei K ein Körper. Eine Funktion | · | : K → ℝ ist eine Betrags­funktion, wenn gilt

|x| ≥ 0

|x|  =  0  ⇔  x = 0

|x · y|  =  |x| · |y|

|x + y| ≤ |x| + |y|

für alle x, y ∈ K.

Beispiel:  Sei K = ℂ der Körper der komplexen Zahlen. Für z ∈ ℂ mit z = a + bi ist der Betrag folgender­maßen definiert:

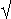|z|  =  Wurzela2 + b2

Mit dieser Betrags­funktion lassen sich die p-Normen im Vektorraum ℂn über ℂ genau wie im ℝn definieren.

Beispiel:  Sei (𝔹, ⊕, ·) der Körper mit den zwei Elementen 0 und 1, der Addition modulo 2 und der Multi­plikation modulo 2. Der Betrag von 0 ∈ 𝔹 sei 0 ∈ ℝ, der Betrag von 1 ∈ 𝔹 sei 1 ∈ ℝ. Diese Zuordnung erfüllt die angegebenen Eigen­schaften einer Betrags­funktion.

Im Vektorraum 𝔹n über 𝔹 lässt sich dann z.B. die 1-Norm (Betrags­summen­norm) definieren. Für einen Vektor x ∈ 𝔹n ist die Norm ||x||1 gleich der Anzahl der Einsen in x; so ist etwa

|| 0 1 0 0 1 1 0 ||1  =  3

In der Codierungs­theorie wird die Betrags­summen­norm in 𝔹n als Hamming-Gewicht bezeichnet.

Metrik

Aus einer Norm in V lässt sich in folgender Weise eine Metrik oder Abstands­funktion d : V × V → ℝ erzeugen:

d(x, y)  =  ||x – y||

für alle x, y ∈ V.

Damit ist jeder normierte Raum auch ein metrischer Raum.

 

Die euklidische Norm erzeugt auf diese Weise den euklidischen Abstand, die 1-Norm den Manhattan-Abstand.

In der Codierungs­theorie ist die vom Hamming-Gewicht erzeugte Metrik der Hamming-Abstand.

Aufgaben

Aufgabe 1:  Sei V ein Vektorraum mit Norm ||  ||. Zeigen Sie unter Benutzung der Rechenregeln in einem Vektorraum, dass für alle x ∈ V gilt

||x||  =  ||-x||

Aufgabe 2:  Zeigen Sie, dass aus den drei Bedingungen der Definition der Norm folgt

||x|| ≥ 0

für alle x ∈ V.

Aufgabe 3:  Sei x ∈ ℝ4 mit x = 1 2 3 4. Berechnen Sie mit Excel die p-Normen ||x||p für p = 1, 2, 3, 5, 8.

 

Weiter mit:   [Metrik]   [Literatur]   oder   [up]

 

H.W. Lang   mail@hwlang.de   Impressum   Datenschutz
Created: 17.03.2000   Updated: 10.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden