Mathematische Grundlagen
Komplexe Zahlen
Die Gleichung x2 + 1 = 0 hat die Lösung x =  -1; dies ist jedoch keine reelle Zahl. Damit Gleichungen dieser Art lösbar sind, wird der Zahlenbereich erweitert zu den komplexen Zahlen.
-1; dies ist jedoch keine reelle Zahl. Damit Gleichungen dieser Art lösbar sind, wird der Zahlenbereich erweitert zu den komplexen Zahlen.
Definition: Eine komplexe Zahl ist eine Zahl der Form
z = a + bi
mit a, b ∈ ℝ sowie i =  -1.
-1.
Hierbei ist a ∈ ℝ der Realteil Re(z) und b ∈ ℝ der Imaginärteil Im(z) der komplexen Zahl z.
Die Menge der komplexen Zahlen wird mit ℂ bezeichnet.
Die reellen Zahlen ℝ sind eine Teilmenge der komplexen Zahlen ℂ, nämlich diejenigen komplexen Zahlen, deren Imaginärteil 0 ist.
Die reellen Zahlen lassen sich als Punkte auf der Zahlengeraden veranschaulichen, die komplexen Zahlen dagegen als Punkte in der komplexen oder gaußschen Zahlenebene. Hierbei wird eine komplexe Zahl z = a + bi als Koordinatenpaar (a, b) angesehen. Als Beispiel ist in Bild 1 die komplexe Zahl 2.5 – 3i in die komplexe Zahlenebene eingezeichnet.
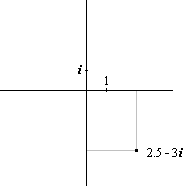
Bild 1: Darstellung einer komplexen Zahl als Punkt in der Ebene
Im Folgenden werden die Regeln für das Rechnen mit komplexen Zahlen angegeben.
Addition
Seien a + bi und c + di komplexe Zahlen. Dann ist
(a + bi) + (c + di) = (a + c) + (b + d)i
Sieht man die komplexen Zahlen a + bi und c + di als Paare (a, b) und (c, d) an, so erfolgt die Addition komponentenweise:
(a, b) + (c, d) = (a+c, b+d)
Beispiel: Es ist
(2.5 – 3i) + (1 + 2i) = 3.5 – i.
Subtraktion
Seien a + bi und c + di komplexe Zahlen. Dann ist
(a + bi) – (c + di) = (a – c) + (b – d)i
Sieht man die komplexen Zahlen a + bi und c + di als Paare (a, b) und (c, d) an, so erfolgt die Subtraktion komponentenweise:
(a, b) – (c, d) = (a-c, b-d)
Multiplikation
Seien a + bi und c + di komplexe Zahlen. Dann ergibt sich das Produkt durch Ausmultiplizieren:
(a + bi) · (c + di) = ac + adi + bci – bd = (ac – bd) + (ad + bc)i
Beispiel: Es ist
(2.5 – 3i) · (1 + 2i) = 8.5 + 2i.
Konjugierte Zahl
Definition: Sei z = a + bi eine komplexe Zahl. Dann ist
z = a – bi
die zu z konjugierte Zahl. Der Imaginärteil wird also einfach negativ genommen.
Offenbar gilt
z = z
Ferner gilt für reelle Zahlen x, also für x ∈ ℝ
x = x
Betrag
Der Betrag einer komplexen Zahl lässt sich als Abstand des entsprechenden Punktes vom Nullpunkt in der komplexen Zahlenebene deuten.
Sei z = a + bi eine komplexe Zahl. Dann ist
 a2 + b2
a2 + b2
der Betrag von z. Der Betrag ist eine nichtnegative reelle Zahl. Der Betrag von z ist genau dann 0, wenn z = 0 ist.
Beispiel: Der Betrag von 2.5 – 3i ist ungefähr 3.095.
Der Betrag einer komplexen Zahl z = a + bi lässt sich mithilfe der konjugierten Zahl z = a – bi ausrechnen. Es gilt
z · z = a2 + b2 = |z|2
Indem also eine komplexe Zahl mit ihrer konjugierten Zahl multipliziert wird, ergibt sich das Quadrat ihres Betrags. Damit ergibt sich der Betrag einer komplexen Zahl z als
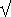 z · z
z · z
Kehrwert
Die konjugierte Zahl spielt auch bei der Berechnung des Kehrwertes einer komplexen Zahl eine Rolle. Zunächst ist ja nicht klar, welche komplexe Zahl der Bruch
| 1 |
| a + bi |
darstellt. Der Trick besteht darin, diesen Bruch mit der konjugierten Zahl des Nenners zu erweitern.
Sei z eine komplexe Zahl mit z ≠ 0. Für den Kehrwert von z gilt
| 1 |
| z |
| 1 · z |
| z · z |
| z |
| |z|2 |
Da |z|2 eine reelle Zahl ist, lässt sich das Ergebnis hierdurch kürzen.
Beispiel:
| 1 |
| 3 + 4i |
| 1 · (3 - 4i) |
| (3 + 4i)·(3 - 4i) |
| 3 - 4i |
| 32 + 42 |
| 3 - 4i |
| 25 |
| 3 |
| 25 |
| 4 |
| 25 |
Bemerkung: Bei einer komplexen Zahl mit dem Betrag 1 ist der Kehrwert gleich der konjugierten Zahl.
Division
Die Division lässt sich auf Multiplikation mit dem Kehrwert zurückführen. Seien w und z komplexe Zahlen mit z ≠ 0. Dann ist
| w |
| z |
| w · z |
| |z|2 |
Regeln
Satz: Für alle w, z ∈ ℂ gilt
w · z = wz
Beweis: Seien w = a + bi und z = c + di. Durch Ausmultiplizieren der entsprechenden konjugierten Zahlen ergibt sich das konjugierte Produkt der Zahlen:
Für x ∈ ℝ gilt x = x. Daher ergibt sich folgendes Korollar:
Korollar: Für alle x ∈ ℝ, z ∈ ℂ gilt
x · z = x · z = xz
Satz: Für alle z ∈ ℂ mit z ≠ 0 gilt
d.h. der konjugierte Kehrwert der Zahl ist gleich dem Kehrwert der konjugierten Zahl.
Beweis: Der Wert 1/|z|2 ist eine reelle Zahl. Mit Hilfe des Korollars und der Formel für den Kehrwert lässt sich der Beweis wie folgt führen:
Mit Hilfe des ersten Satzes lässt sich folgender Satz zeigen:
Satz: Für alle w, z ∈ ℂ gilt
|w| · |z| = |wz|
Beweis: Es ist
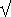 w·w ·
w·w · 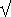 z·z =
z·z = 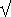 w·z·w·zSatz 1 =
w·z·w·zSatz 1 = 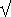 wz · wzFormel für den Betrag = |wz|
wz · wzFormel für den Betrag = |wz|
Komplexe Zahl als Exponent
Eine natürliche Zahl n als Exponent bei einer Potenz, zum Beispiel an, bedeutet ja, dass die Basis a entsprechend oft, also n-mal mit sich selbst multipliziert wird:
an = a · a · ... · a (n-mal)
Hieraus ergeben sich die Regeln der Potenzrechnung:
an · am = a · a · ... · a · a · a · ... · a (insgesamt n+m-mal) = an+m
Für n < m gilt
| a · a · ... · a (n-mal) |
| a · a · ... · a (m-mal) |
| 1 |
| a · a · ... · a (m-n-mal) |
| 1 |
| am-n |
(an)m = (a · a · ... · a) · ... · (a · a · ... · a) (insgesamt n·m-mal) = an·m
Bei anderen als natürlichen Zahlen ist diese anschauliche Bedeutung nicht mehr haltbar; stattdessen wird die Bedeutung in geeigneter Weise definiert.
a0 = 1
| 1 |
| ax |
a1/2 =  a
a
Was aber ist a i ?
Hier geht es nicht anders, als die Potenzreihen-Entwicklung der Exponentialfunktion ex heranzuziehen:
| x0 |
| 0! |
| x1 |
| 1! |
| x2 |
| 2! |
| x3 |
| 3! |
| x4 |
| 4! |
Mit x = i ergibt sich
| -1 |
| 2! |
| -i |
| 3! |
| 1 |
| 4! |
| i |
| 5! |
| 1 |
| 2! |
| 1 |
| 4! |
| 1 |
| 3! |
| 1 |
| 5! |
Hierbei wird die Potenzreihen-Entwicklung der Kosinus- und Sinusfunktion verwendet.
Mit 2 = eln(2) ergibt
2 i = ei·ln(2) = cos(ln(2)) + i·sin(ln(2))
Wenn der Exponent eine komplexe Zahl ist wie zum Beispiel 3 + 2i, dann ist
23 + 2i = 23 · 22i = 8 · e i·2·ln(2) = 8 · (cos(2·ln(2)) + i·sin(2·ln(2)))
Polarkoordinaten
Die komplexe Zahl cos(x) + i·sin(x) liegt in der komplexen Ebene im Abstand 1 vom Nullpunkt mit einem Winkel x.
Für die komplexe Zahl au + iv bedeutet dies:
- Betrag: au
- Winkel: v·ln(a)
Weiter mit: [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 13.01.2004 Updated: 10.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden