Mathematische Grundlagen
Metrik
Definition: Sei M eine Menge. Eine Abbildung d : M × M → ℝ heißt Metrik (Abstandsfunktion), wenn für alle u, v, w ∈ M folgendes gilt:
d(u, v) = 0 ⇔ u = v
d(u, v) = d(v, u)
d(u, v) ≤ d(u, w) + d(w, v)
Stellen wir uns die Elemente von M als Punkte vor, so besagen die Bedingungen, dass jeder Punkt zu sich selbst den Abstand 0 hat, aber sonst zu keinem anderen Punkt, dass Hin- und Rückweg zwischen zwei Punkten gleich lang sind und dass der direkte Weg nie länger ist als ein Umweg.
Die letzte Bedingung ist bekannt als die Dreiecksungleichung. Aus den drei Bedingungen folgt d(u, v) ≥ 0 für alle u, v ∈ M, d.h. negative Abstände gibt es nicht.
Beispiel: Sei M die Menge der Punkte (x, y) in der Ebene.
Dann ist der euklidische Abstand eine Metrik (Bild 1a):
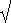(x1 – x2)2 + (y1 – y2)2
Ebenso ist der Manhattan-Abstand eine Metrik (Bild 1b):
d( (x1, y1), (x2, y2) ) = |x1 – x2| + |y1 – y2|
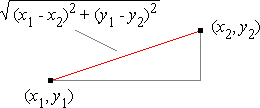
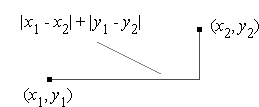
Bild 1: Euklidischer Abstand (a) und Manhattan-Abstand (b) zwischen zwei Punkten
Beispiel:
In der Codierungstheorie ist der Hamming-Abstand eine Metrik.
Der Hamming-Abstand zweier gleichlanger Wörter ist gleich der Anzahl der Positionen, an denen sie sich unterscheiden.
So haben etwa 01101 und 00111 den Hamming-Abstand 2, da sie sich im 2. und im 4. Bit unterscheiden. Die Wörter THEORIE und THEODOR haben den Hamming-Abstand 3.
Aufgabe 1:
Zu zeigen: Ist d eine Metrik, so gilt d(u, v) ≥ 0 für alle u, v ∈ M.
Weiter mit: [Teilbarkeit, Kongruenz] [Literatur] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 17.03.2000 Updated: 10.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden