Graphenalgorithmen

Minimaler Spannbaum

Gegeben ist ein zusammen­hängender ungerichteter Graph G = (V, E), dessen Kanten mit Gewichten markiert sind. Gesucht ist ein Baum T, der den Graphen "aufspannt" und minimales Kanten­gewicht hat. Der Baum T spannt G auf, wenn er ein Teilgraph von G ist und alle Knoten von G enthält (Bild 1).

 

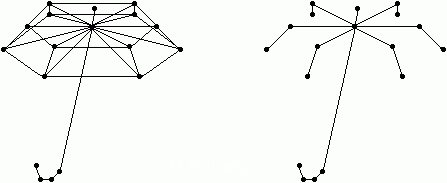
Bild 1: Graph G und Spannbaum von G 

Bild 1: Graph G und Spannbaum von G

 

Grundlagen

Definition:  Sei G = (V, E) ein ungerichteter Graph. Ein Teilgraph T = (V, E') heißt Spannbaum von G, wenn er ein Baum ist und aus allen Knoten von G besteht.

Definition:  Sei G = (V, E) ein ungerichteter Graph. Eine Abbildung w : E → ℝ heißt Kanten­gewichtung, wenn für alle (i, j) ∈ E gilt:

w(i, j) ≥ 0   und

w(i, j) = w(j, i)

Das Gewicht w einer Kante (i, j) lässt sich beispiels­weise als Länge der Kante inter­pretieren, d.h. als Entfernung zwischen benachbarten Knoten i und j.

Definition:  Sei G = (V, E) ein ungerichteter Graph mit einer Kanten­gewichtung w. Das Gewicht w(G) des Graphen ist gleich der Summe der Gewichte aller seiner Kanten:

w(G) =  Summee ∈ E    w(e)

Ein Spannbaum T = (V, E') von G heißt minimaler Spannbaum von G, wenn sein Gewicht minimal ist, d.h. wenn für alle Spannbäume T' von G gilt:

w(T') ≥ w(T)

Berechnung eines minimalen Spannbaums

Die Idee des Verfahrens von Prim [Pri 57] zur Berechnung eines minimalen Spannbaums ist, den Baum ausgehend von einem Startknoten s Schritt für Schritt aufzubauen. Der Startknoten s kann beliebig gewählt werden.

Zu jedem Zeitpunkt besteht die Menge aller Knoten V aus drei disjunkten Mengen (Bild 2):

Die Strategie ist nun, nach einem Kandidaten v zu suchen, der durch eine Kante minimalen Gewichts mit T verbunden ist. Diese Kante wird zum Baum hinzu­genommen, der Kandidat v wird zu T hinzu­genommen und aus K entfernt. Anschließend wird die Menge der Kandidaten K aktualisiert, indem die zu v benachbarten Knoten hinzu­genommen werden, die noch nicht zu T gehören.

 

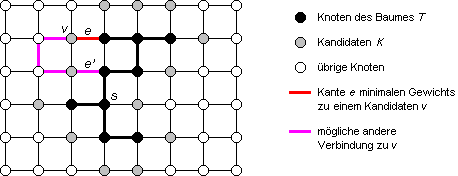
Bild 2: Graph mit Knotenmengen T und K 

Bild 2: Graph mit Knotenmengen T und K

 

Die Korrektheit dieses Vorgehens folgt daraus, dass die Kante e minimalen Gewichts, die von T zu einem Kandidaten v führt, sicherlich zu einem minimalen Spannbaum gehört und daher zum Baum hinzu­genommen werden kann.

Angenommen, dies wäre falsch, und in jedem tat­sächlichen minimalen Spannbaum S würde ein anderer Weg von T zu v führen. Die erste Kante e' eines solchen Weges müsste aber auch zu einem Kandidaten führen, hätte also mindestens dasselbe Gewicht wie e. Indem nun in S die Kante e' gegen e ausgetauscht wird, entsteht ein Spannbaum, der höchstens genauso viel wiegt wie S, also minimal ist. Also gehört e doch zu einem minimalen Spannbaum und kann in diesem Schritt zum Baum hinzu­genommen werden.

Greedy-Strategie

Die Vorgehens­weise des Algorithmus wird als Greedy-Strategie bezeichnet (engl.: greedy – gierig). Eine solche "Nimm-was-du-kriegen-kannst"-Strategie führt allerdings nicht bei allen Optimierungsproblemen zum Erfolg. Manchmal ist es besser, zunächst Verzicht zu üben, um dafür später umso reichlicher belohnt zu werden.

Die Konstruktion eines Huffman-Codes ist ein weiteres Beispiel für die erfolgreiche Anwendung der Greedy-Strategie.

Implementierung

Welche Art der Implementierung am günstigsten ist, hängt von der Daten­struktur ab, die für die Darstellung des Graphen verwendet wird. Welche Daten­struktur am günstigsten ist, hängt wiederum davon ab, ob die darzustellenden Graphen typischer­weise viele, z.B. Ω(n2) oder wenige, z.B. nur O(n) Kanten haben (n = |V|, Anzahl der Knoten des Graphen).

Bei wenigen Kanten ist eine Darstellung in Form von Adjazenz­listen vorteilhaft. Dann lässt sich die im Folgenden skizzierte Implementierung des Algorithmus mit einer Prioritäten­liste anwenden. Bei vielen Kanten ist eine Darstellung als Adjazenz­matrix geeignet, und der Algorithmus lässt sich ohne Verwendung einer Prioritäten­liste implementieren.

a) mit Prioritäten­liste

Eine Prioritäten­liste (engl.: priority queue) ist eine Daten­struktur mit Operationen insert und extract. Die Operation insert fügt einen Eintrag mit einer bestimmten Priorität in die Liste ein, die Operation extract liefert den Eintrag mit der höchsten Priorität und entfernt ihn aus der Liste. Mit Hilfe der Daten­struktur eines Heaps lässt sich eine Prioritäten­liste mit m Einträgen so implementieren, dass die Operationen insert und extract nur jeweils log(m) Schritte benötigen.

Das Verfahren zur Berechnung eines minimalen Spannbaums lässt sich implementieren, indem die Kandidaten in einer Prioritäten­liste P gehalten werden. Als Priorität wird jeweils der Abstand zum Baum genommen. Mit extract wird dann jeweils der Knoten minimalen Abstands zum Baum ermittelt und, sofern er nicht bereits zum Baum gehört, zum Baum hinzu­genommen.

Jedes Mal, wenn ein neuer Knoten zum Baum hinzukommt, werden seine Nachbar­knoten, sofern sie noch nicht zum Baum gehören, mit insert in die Prioritäten­liste eingefügt.

Da jeder Knoten u, der zum Baum hinzu­genommen wird, maximal für jeden seiner Nachbar­knoten v eine insert-Operation verursacht, entsteht maximal für alle benachbarten Knotenpaare (u, v), d.h. für alle Kanten, eine insert-Operation (und eine zugehörige extract-Operation). Die Komplexität des Verfahrens liegt also in O(m log(m)), wobei m = |E| die Anzahl der Kanten des Graphen ist.

Eine ausführliche Beschreibung dieses Verfahrens ist im Zusammenhang mit der Berechnung der kürzesten Wege in einem Graphen beschrieben.

b) ohne Prioritäten­liste

Das Verfahren lässt sich auch ohne Prioritäten­liste mit Komplexität O(n2) realisieren. Dies ist dann günstiger, wenn die Anzahl der Kanten des Graphen in Ω(n2) liegt.

 

Algorithmus Minimaler Spannbaum

Eingabe:

Zusammenhängender ungerichteter Graph G = (V, E) mit Kantengewichtung w

Ausgabe:

Minimaler Spannbaum von G; für jeden Knoten v (außer der Wurzel 0) bedeuten predecessor(v) den Vorgänger von v im Spannbaum und distance(v) das entsprechende Gewicht der Kante zum Vorgänger

Methode:

  1. für alle v ∈ V wiederhole
    1. setze distance(v) = ∞

    setze u = 0     // Startknoten 0

    setze distance(u) = 0

    setze predecessor(u) = -1

    setze T = {u}

    solange T ≠ V wiederhole

    1. für alle Knoten v mit v ∉ T wiederhole
      1. wenn distance(v) > w(u, v) dann
        1. setze distance(v) = w(u, v)

          2. setze predecessor(v) = u

      suche u ∉ T mit distance(u) minimal

      setze T = T ∪ {u}

 

Programm

Die Implementierung des oben­stehenden Algorithmus ist gekapselt in einer Klasse MinimumSpanningTree. Im Konstruktor der Klasse wird ein ungerichteter Graph mit Kanten­markierungen übergeben. Die Klasse MinimumSpanningTree ist von der Klasse RootedTree abgeleitet, die alle grund­legenden Daten und Methoden für den Aufbau eines Baumes enthält.

Abweichend von dem ursprüng­lichen Algorithmus ist die Gewichtsfunktion w nicht nur für die Kanten des Graphen definiert, sondern für alle Paare von Knoten (u, v). Ist (u, v) keine Kante, so ist das Gewicht der Kante gleich noedge = ∞. Dies führt zu einem robusten Verhalten des Verfahrens auch in dem Fall, dass der Graph nicht zusammen­hängend ist; es wird dann für jede Zusammenhangs­komponente der minimale Spannbaum berechnet.

public class MinimumSpanningTree extends RootedTree
{
    private WeightedUndirectedGraph graph;

    public MinimumSpanningTree(WeightedUndirectedGraph graph)
    {
        super(graph.getSize());
        this.graph=graph;
        computeMinimumSpanningTree(0);  // Startknoten 0
    }

    public void computeMinimumSpanningTree(int u_)
    {
        int k, u, v;
        double w, m;

        u=u_;    // Startknoten
        setDistance(u, 0);
        toTree(u);

        for (k=1; k<n; k++)    // alle weiteren Knoten behandeln
        {
            // Kandidaten aktualisieren
            for (v=0; v<n; v++)
            {
                w=graph.getWeight(u, v);
                if (!inTree(v) && getDistance(v)>w)
                {
                    setDistance(v, w);
                    setPredecessor(v, u);
                }
            }

            // u nicht in T mit u minimal suchen
            m=graph.noedge;
            for (v=0; v<n; v++)
                if (!inTree(v) && getDistance(v)<=m)
                {
                    m=getDistance(v);
                    u=v;
                }

            // u zu T hinzufügen
            toTree(u);
        }
    }

}    // end class MinimumSpanningTree

Literatur

Originalartikel:

[Pri 57]   R.C. Prim: Shortest Connection Networks and some Generalizations. Bell System Technical Journal, Vol. 36, 1389-1401 (1957)

 

Bücher

 

Weiter mit:   [Kürzeste Wege]   [Literatur]   oder   [up]

 

H.W. Lang   mail@hwlang.de   Impressum   Datenschutz
Created: 29.01.1998   Updated: 20.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden