Graphenalgorithmen

Kürzeste Wege

Problem

Gegeben ist ein zusammen­hängender ungerichteter Graph mit einer Kanten­gewichtung. Gesucht sind die kürzesten Wege von einem bestimmten Startknoten zu allen anderen Knoten des Graphen.

Der Floyd-Algorithmus löst das Problem mit der Zeit­komplexität Θ(n3). Er berechnet aber sogar die kürzesten Wege von allen Knoten zu allen anderen Knoten.

Wenn nur die kürzesten Wege von einem bestimmten Startknoten zu allen anderen Knoten gesucht sind, lässt sich das Problem mit geringerem Aufwand lösen.

Idee

Die kürzesten Wege von einem Startknoten zu allen anderen Knoten eines zusammen­hängenden ungerichteten Graphen bilden einen Baum mit dem Startknoten als Wurzel.

Bei einem Graphen ohne Kanten­gewichtung kann dieser Baum durch eine Breitensuche aufgebaut werden. Es wird mit dem Startknoten begonnen, und dann werden alle Nachbar­knoten hinzu­genommen, dann deren Nachbar­knoten, soweit sie noch nicht zum bisher berechneten Baum dazugehören usw. Es kommen also zuerst alle Knoten der Entfernung 1 hinzu, dann alle der Entfernung 2 usw.

Bei einem Graphen mit Kanten­gewichtung ist die Situation anders. Die Entfernung eines Knotens zur Wurzel berechnet sich nicht nach der minimalen Anzahl der Kanten eines Weges dorthin, sondern nach der minimalen Summe der Kanten­gewichte eines Weges zur Wurzel.

Entsprechend anders wird der Baum der kürzesten Wege berechnet. Zum jeweils schon berechneten Baum kommt als nächster immer derjenige Knoten hinzu, der die geringste Entfernung zur Wurzel hat, wobei alle Knoten betrachtet werden, die Nachbarn eines Baumknotens sind und selbst noch nicht zum Baum dazugehören; diese werden als die Kandidaten bezeichnet. Dieses Vorgehen ist ähnlich wie bei der Berechnung des minimalen Spannbaums.

Beispiel:  Der Algorithmus hat bereits folgenden Baum der kürzesten Wege vom Startknoten zu einigen anderen Knoten konstruiert (Bild 1). Der Abstand vom Startknoten ist jeweils in den Knoten notiert. Drei Kandidaten stehen zur Auswahl, um den Baum weiter zu vervollständigen.

Die Wahl fällt auf den unteren Kandidaten und die mit 3 markierte Kante, denn hierdurch ergibt sich der Abstand 10 für den Kandidaten, und dieser ist für die drei Kandidaten minimal.

 

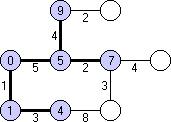
Bild 1: Auswahl des nächsten Kandidaten 

Bild 1: Auswahl des nächsten Kandidaten

 

Algorithmus

Bei der Breitensuche genügt eine Schlange (queue) als Daten­struktur, um die Kandidaten zu speichern und in der richtigen Reihenfolge zum schon berechneten Baum hinzuzunehmen. Wenn die Kanten­gewichte jedoch nicht alle 1 sind, sondern unter­schiedlich sind, ist hierzu eine Prioritäten­liste (priority queue) erforderlich. In eine Prioritäten­liste werden mit insert Elemente eingefügt, mit extract wird jeweils das Element höchster Priorität entnommen und zurück­gegeben.

Bei der Berechnung der kürzesten Wege werten wir als höchste Priorität die kleinste Entfernung zum Startknoten. Als Elemente werden die Kandidaten in die Prioritäten­liste aufgenommen. Zu jedem Kandidaten v bedeutet distance(v) die bisher gefundene kürzeste Entfernung zum Startknoten und predecessor(v) den zugehörigen Vorgänger im Baum.

 

Algorithmus Kürzeste Wege

Eingabe:

Zusammenhängender ungerichteter Graph G = (V, E) mit Kantengewichtung w, Startknoten s

Ausgabe:

Baum der kürzesten Wege in G vom Startknoten s zu allen anderen Knoten

Methode:

  1. setze distance(s) = 0

    2. setze predecessor(s) = -1

    füge Startknoten s mit Priorität 0 in die Prioritätenliste ein

    solange die Prioritätenliste nicht leer ist wiederhole

    1. entnimm obersten Knoten u aus der Prioritätenliste

      2. wenn u noch nicht zum Baum dazugehört dann

      1. füge Knoten u zum Baum hinzu

        2. für alle Nachbarn v von u wiederhole

        1. setze d = distance(u) + w(u, v)

          2. wenn d  <  distance(v) dann

          1. setze distance(v) = d

            2. setze predecessor(v) = u

            füge Knoten v mit Priorität d in die Prioritätenliste ein

 

Implementierung

Das folgende Java-Programm implementiert den Algorithmus Kürzeste Wege. Für das Durchlaufen aller Nachbar­knoten eines Knotens wird ein NeighbourIterator verwendet. Eine Implementierung der Prioritäten­liste ist unter PriorityQueue zu finden.

Die Klasse ShortestPathsTree basiert auf der Klasse RootedTree; diese stellt alle erforder­lichen Daten und Methoden zum Aufbau des Baums der kürzesten Wege zur Verfügung. Die Werte distance(v) und predecessor(v) werden dort für jeden Knoten v mithilfe von Markern gespeichert.

 

import java.util.Iterator;
import basic.PriorityQueue;

public class ShortestPathsTree extends RootedTree
{
    private WeightedUndirectedGraph graph;     // Graph mit Kantengewichtung
    private int s;           // Startknoten

    public ShortestPathsTree(WeightedUndirectedGraph graph, int s)
    {
        super(graph.getSize());
        this.graph=graph;
        this.s=s;
        computeShortestPaths();
    }

    private void computeShortestPaths()
    {
        int u, v;
        double d;
        Iterator<Integer> it;
        PriorityQueue<Integer> pq=new PriorityQueue<Integer>(-1);  // höchste Priorität: Minimum
        setDistance(s, 0);        // Startknoten s
        setPredecessor(s, -1);
        pq.insert(0, s);
        while (!pq.isEmpty())
        {
            u=pq.extractObj();
            if (!inTree(u))
            {
                toTree(u);
                it=graph.getNeighbourIterator(u);
                while (it.hasNext())
                {
                    v=it.next();
                    d=getDistance(u)+graph.getWeight(u, v);
                    if (d<getDistance(v))
                    {
                        setDistance(v, d);
                        setPredecessor(v, u);
                        pq.insert(d, v);
                    }
                }
            }
        }
    }

} // end class ShortestPathsTree

 

Analyse

Gegeben sei ein Graph G = (V, E) mit n Knoten und m Kanten. Wir betrachten die Anzahl der insert-Operationen in die Prioritäten­liste. Jeder Knoten u, der mit toTree(u) zum Baum hinzu­genommen wird, verursacht maximal für jeden seiner Nachbar­knoten v eine insert-Operation. D.h. maximal gibt es für alle benachbarten Knotenpaare (u, v), d.h. für alle Kanten, eine insert-Operation, also O(m) insert-Operationen (und natürlich ebenso viele extract-Operationen).

Die Prioritäten­liste kann auf O(m) Einträge anwachsen; die Operationen insert und extract dauern somit O(log(m)) Schritte. Die Zeit­komplexität des Algorithmus beträgt daher O(m log(m)).

Für Graphen mit wenigen Kanten ist dies ein günstiges Ergebnis. Beispiels­weise enthält ein gitterartig verbundener Graph nur O(n) Kanten, somit ergibt sich hier eine Zeit­komplexität von O(n log n). Im Allgemeinen kann ein Graph jedoch Θ(n2) Kanten enthalten, damit ergibt sich eine Zeit­komplexität von O(n2 log n). Hier ist dann das im Folgenden angegebene Verfahren von Dijkstra mit der Zeit­komplexität von O(n2) günstiger.

Aufgaben

Aufgabe 1:  In der angegebenen Implementierung werden die kürzesten Wege vom Startknoten s zu allen Knoten des Graphen berechnet. Wenn nur der kürzeste Weg vom Startknoten s zu einem bestimmten Zielknoten t berechnet werden soll, lässt sich das Verfahren abkürzen. An welcher Stelle greifen Sie hierzu in der Methode computeShortestPaths ein, wenn ein bestimmter Zielknoten t vorgegeben ist? Programmieren Sie diese Änderung und führen Sie entsprechende Tests durch.

 

Weiter mit:   [Algorithmus von Dijkstra]   oder   [up]

 

H.W. Lang   mail@hwlang.de   Impressum   Datenschutz
Created: 03.03.2002   Updated: 20.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden