Mathematische Grundlagen
Graph
Knoten und Kanten
Definition: Ein (gerichteter) Graph ist ein Paar G = (V, E), hierbei ist V eine endliche Menge von Knoten und E ⊆ V × V eine Relation auf V, die Menge der Kanten.
In der grafischen Darstellung des Graphen werden die Knoten als Punkte oder Kreise gezeichnet, die Kanten als Pfeile, wobei ein Pfeil vom Knoten u ∈ V zum Knoten v ∈ V zeigt, wenn (u, v) ∈ E.
Beispiel: G = (V, E) mit V = {0, 1, 2, 3, 4} und
E = {(0,1), (0,2), (3,0), (2,0), (1,2)}
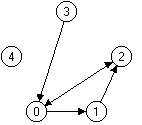
Bild 1: Darstellung des Graphen G
Definition: Sei G = (V, E) ein Graph und (u, v) ∈ E eine Kante von Knoten u nach Knoten v. Dann ist v direkter Nachfolger von u und u direkter Vorgänger von v.
Der Ausgangsgrad o(u) eines Knotens u ist gleich der Anzahl seiner direkten Nachfolger, d.h.
o(u) = | { w | (u, w) ∈ E } |.
Der Eingangsgrad i(u) eines Knotens u ist gleich der Anzahl seiner direkten Vorgänger, d.h.
i(u) = | { v | (v, u) ∈ E } |.
Ein Knoten u heißt isoliert wenn o(u) = i(u) = 0 gilt.
Eine Kante (u, u) von einem Knoten u zu sich selbst heißt Schlinge.
Beispiel: In G ist Knoten 0 direkter Nachfolger von Knoten 3; Knoten 2 hat den Ausgangsgrad 1 und den Eingangsgrad 2. Knoten 4 ist isoliert. G hat keine Schlingen.
Pfad
Definition: Ein Pfad (oder Kantenzug) in einem Graphen ist eine endliche Folge von Kanten
p = (u0, v0) ... (um-1, vm-1)
mit m ∈ ℕ0 und vi-1 = ui für alle i ∈ {1, ..., m-1}.
Hierbei ist m die Länge des Pfades. Wir identifizieren Kanten und Pfade der Länge 1. Der Pfad der Länge 0 heißt der leere Pfad, wir bezeichnen ihn mit λ. Der Knoten u0 heißt Anfangsknoten von p, der Knoten vm-1 heißt Endknoten. Alle anderen Knoten von p heißen innere Knoten.
Beispiel: Pfade in obigem Graphen G sind
p1 = (3,0) (0,2) (2,0) (0,2)
p2 = (0,1) (1,2) (2,0)
p3 = (3,0)
p4 = (3,0) (0,1) (1,2) (2,0)
Der Pfad p1 hat die Länge 4, der Pfad p3 hat die Länge 1. Im Pfad p2 ist der Knoten 0 zugleich Anfangs- und Endknoten. In p4 ist Knoten 0 sowohl innerer Knoten als auch Endknoten.
Definition: Sei p = (u0, v0) ... (um-1, vm-1) ein Pfad in einem Graphen G.
p heißt einfach, wenn er keine Kante mehrfach durchläuft, d.h. wenn alle (ui, vi) paarweise verschieden sind (i = 0, ..., m-1).
p heißt Zyklus, wenn er geschlossen ist, d.h. wenn vm-1 = u0 gilt.
p heißt Weg, wenn er keinen Knoten mehrfach durchläuft, d.h. wenn alle ui untereinander und alle vj untereinander paarweise verschieden sind (i, j = 0, ..., m-1).
p heißt Kreis, wenn er ein Weg ist und geschlossen ist, d.h. ein Zyklus ist.
Beispiel: Der Pfad p1 aus dem vorigen Beispiel ist kein einfacher Pfad, weil er die Kante (0,2) zweimal enthält. Der Pfad p4 ist ein einfacher Pfad, aber kein Weg, weil er den Knoten 0 mehrmals durchläuft. Der Pfad p2 ist ein Zyklus und sogar ein Kreis.
Der leere Pfad λ ist einfach und ist auch ein Weg, aber kein Zyklus und kein Kreis. Er hat keinen Anfangs- und keinen Endknoten und keine inneren Knoten.
Satz: Sei G = (V, E) ein Graph mit n Knoten, d.h. |V| = n. Dann hat jeder Weg in G höchstens die Länge n.
Beweis: Sei p = (u0, v0) ... (um-1, vm-1) ein Pfad der Länge m > n. Dann können nicht alle ui verschieden sein, da es nur n Knoten gibt. Also ist p kein Weg.
Satz: Wenn es in G einen Pfad von u nach v gibt, dann gibt es auch einen Weg von u nach v.
Beweis: Sei p = (u0, v0) ... (um-1, vm-1) ein Pfad von u nach v. Aus p wird wie folgt ein Weg konstruiert:
Solange p kein Weg ist wiederhole:
- Suche einen Knoten w, der in p zweimal vorkommt, d.h.
- w = ui und w = vj mit i ≤ j;
- Streiche das Stück von ui nach vj in p, d.h. setze
- p = (u0, v0) ... (ui-1, vi-1) (uj+1, vj+1) ... (um-1, vm-1);
Im folgenden Bild 2 ist ein Pfad dargestellt, der einen Knoten ui = vj zweimal durchläuft. Indem die Schleife von ui nach vj entfernt wird, entsteht ein Weg.
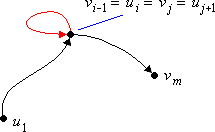
Bild 2: Pfad, der einen Knoten zweimal durchläuft
Baum
Definition: Ein gerichteter Graph T = (V, E) ist ein Baum, wenn
- er genau einen Knoten mit Eingangsgrad 0 enthält; dieser Knoten ist die Wurzel des Baumes,
- alle anderen Knoten den Eingangsgrad 1 haben, und
- er keine Zyklen enthält.
Definition: Sei T ein Baum. Ein Knoten b heißt Blatt, wenn er keine Nachfolger hat; alle anderen Knoten heißen innere Knoten des Baumes.
Die Tiefe d(v) eines Knotens v ist die Länge des Weges von der Wurzel r nach v. Die Tiefe d(T) des Baumes ist die maximale Tiefe der Knoten.
Definition: Ein Baum T ist ein binärer Baum, wenn jeder Knoten einen Ausgangsgrad von höchstens 2 hat.
Definition: Ein binärer Baum T heißt fast vollständig, wenn
- alle Knoten der Tiefe < d(T)-1 den Ausgangsgrad 2 haben, und
- höchstens ein Knoten den Ausgangsgrad 1 hat.
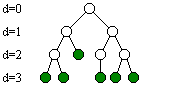
Bild 3: Fast vollständiger binärer Baum mit 12 Knoten
Bei einem fast vollständigen binären Baum darf also die unterste Schicht unvollständig sein (Bild 3).
Satz: Ein vollständiger oder ein fast vollständiger binärer Baum T mit n Knoten hat eine Tiefe von
d(T)) = int(log2(n)).
In der Informatik werden Bäume falsch herum gezeichnet: die Wurzel ist oben, die Blätter sind unten. Die Pfeilspitzen an den Kanten werden dann weggelassen; die Kanten sind immer von oben nach unten gerichtet (Bild 3).
Ungerichteter Graph
Ein ungerichteter Graph lässt sich als Spezialfall eines gerichteten Graphen auffassen, nämlich als ein gerichteter Graph, bei dem die Kanten stets in beide Richtungen verlaufen. Dann können in der grafischen Darstellung die Pfeilspitzen auch weggelassen werden (Bild 4).
Definition: Ein gerichteter Graph G = (V, E) ist ein ungerichteter Graph, wenn seine Kantenrelation E symmetrisch ist, d.h. wenn gilt:
E = E -1.
Ein Graph ist also ungerichtet, wenn für alle Kanten (u, v) gilt: (v, u) ist ebenfalls Kante.
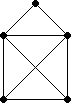
Bild 4: Ungerichteter Graph
Zwei Knoten, die durch eine Kante verbunden sind, werden als benachbart bezeichnet. Die Anzahl der zu einem Knoten u benachbarten Knoten ist der Grad des Knotens u.
Definition: Sei G = (V, E) ein ungerichteter Graph ohne Schlingen.
G heißt zusammenhängend, wenn es in G von jedem Knoten u zu jedem anderen Knoten v mindestens einen Weg gibt.
G heißt kreisfrei, wenn es in G von jedem Knoten u zu jedem anderen Knoten v höchstens einen Weg gibt.
G ist ein Baum, wenn G zusammenhängend und kreisfrei ist, d.h. wenn es in G von jedem Knoten u zu jedem anderen Knoten v genau einen Weg gibt.
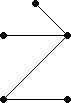
Bild 5: Ungerichteter Baum
Ein ungerichteter Baum hat keine definierte Wurzel. Jeder Knoten kann die Rolle der Wurzel annehmen.
Definition: Sei G = (V, E) ein ungerichteter Graph ohne Schlingen. Ein maximaler zusammenhängender Teilgraph von G heißt Zusammenhangskomponente (connected component) von G.
Definition: Sei G = (V, E) ein ungerichteter Graph ohne Schlingen. G heißt vollständig, wenn jeder Knoten mit jedem anderen Knoten durch eine Kante verbunden ist.
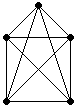
Bild 6: Vollständiger Graph mit 5 Knoten
Ein vollständiger Graph mit n Knoten hat n·(n-1)/2, also Θ(n2) ungerichtete Kanten.
Definition: Sei G = (V, E) ein ungerichteter Graph. Ein Graph G' = (V', E') heißt Teilgraph von G, wenn er aus gewissen Knoten von G und Kanten von G zwischen diesen Knoten besteht und wenn er ungerichtet ist, d.h. wenn gilt
V' ⊆ V,
E' ⊆ E ∩ V' × V' und
E' = E' -1 .
Markierte Graphen
Definition: Sei G = (V, E) ein Graph und A eine Menge. Eine Abbildung
w : V → A,
die jedem Knoten v ∈ V ein Element w(v) ∈ A zuordnet, heißt Knotenmarkierung.
Definition: Sei G = (V, E) ein (gerichteter) Graph und A eine Menge. Eine Abbildung
w : E → A,
die jeder Kante e ∈ E ein Element w(e) ∈ A zuordnet, heißt Kantenmarkierung.
Ist auf der Menge A eine Verknüpfung • definiert und bildet die Menge A mit dieser Verknüpfung ein Monoid (A, • , 1) mit neutralem Element 1, so lässt sich die Markierung der Kanten zu einer Markierung der Pfade in folgender Weise erweitern:
w(λ) = 1 und
w(pe) = w(p) • w(e)
für alle Pfade p und alle Kanten e. Hierbei bezeichnet λ den Pfad der Länge 0.
Beispiel: Sei A = ℕ0. Als Kantenmarkierung w wählen wir die Abbildung, die jeder Kante des Graphen die Zahl 1 zuordnet. Die Menge ℕ0 bildet mit der Operation + und dem neutralen Element 0 ein Monoid. Daher lässt sich die Markierung der Kanten zu einer Markierung der Pfade erweitern:
w(λ) = 0 und
w(pe) = w(p) + w(e)
für alle Pfade p und alle Kanten e.
Somit wird in diesem Beispiel jedem Pfad p durch die Markierung w(p) seine Länge zugeordnet.
Aufgaben
Aufgabe 1: Sei T = (V, E) ein gerichteter Graph. Beweisen Sie unter Benutzung der oben angegebenen Definition für einen (gerichteten) Baum:
T ist ein Baum genau dann, wenn es einen Knoten w ∈ V gibt, von dem aus zu allen anderen Knoten aus V jeweils genau ein Pfad hinführt.
Literatur
Die Mathematik, die Sie in der Informatik brauchen, finden Sie beispielsweise in folgenden Büchern. Wenn Sie noch am Anfang stehen, ist empfehlenswert:
[Lan 21] H.W. Lang: Vorkurs Informatik für Dummies. Wiley (2021)
Lesen Sie zum Thema Graphen auch Kapitel 16 in meinem Buch Vorkurs Informatik für Dummies.
Weiter mit: [Gruppe] [Literatur] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 29.01.1998 Updated: 10.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden
