Graphenalgorithmen

Zusammenhangskomponenten eines Graphen

Ein ungerichteter Graph besteht aus Knoten und Kanten, wobei die Kanten bestimmte Knoten verbinden. Dabei muss nicht unbedingt ein insgesamt zusammenhängendes Gebilde entstehen. Bild 1 zeigt einen Graphen mit 7 Knoten, der nicht zusammenhängend ist. Er besteht aus zwei Zusammenhangskomponenten, d.h. zwei Teilen, die jeweils für sich zusammenhängend sind.

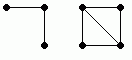
Bild 1: Ein Graph mit 7 Knoten, der nicht zusammenhängend ist

Die Zusammenhangskomponenten eines Graphen lassen sich mit Hilfe der Tiefensuche bestimmen.

Gegeben ist ein nichtleerer zusammenhängender ungerichteter Graph. Die Tiefensuche (depth-first search) ist ein Verfahren, das systematisch die Struktur des Graphen erkundet; es wird im Folgenden beschrieben.

Die Tiefensuche lässt sich sehr leicht rekursiv implementieren. Zu Beginn wird ein Startknoten v gewählt.

Funktion depthFirstSearch(v)

Methode:

markiere den Knoten v
für alle Nachbarknoten w von v wiederhole

wenn w noch nicht markiert ist dann

depthFirstSearch(w)

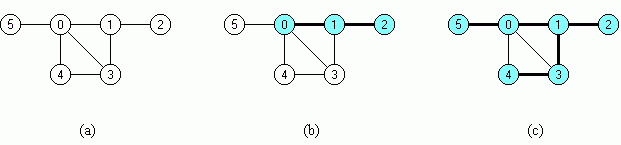
Bild 2: Tiefensuche in einem Graphen G

Bild 2a zeigt als Beispiel einen Graphen G mit 6 Knoten. Als Startknoten wird der Knoten 0 gewählt; dieser wird markiert. Mit dem Nachbarn 1 wird fortgefahren; dieser wird ebenfalls markiert. Werden nun die Nachbarn von 1 betrachtet, so hat 0 bereits eine Markierung, also wird mit dem nächsten Nachbarn 2 fortgefahren; dieser wird als nächstes markiert. Bild 2b zeigt diese Situation. Die Kanten, die zu den jeweils neu markierten Knoten führen, sind fett gezeichnet.

Im weiteren Verlauf des Verfahrens wird festgestellt, dass Knoten 2 keine Nachbarn hat, die noch nicht markiert sind. Der entsprechende Aufruf von depthFirstSearch ist daher hier abgeschlossen und es wird mit dem nächsten Nachbarn des Knotens 1 fortgefahren, also mit Knoten 3.

Vom Knoten 4 schließlich ist wiederum kein Knoten mehr erreichbar, der noch nicht markiert ist. Hier enden nun alle rekursiven Aufrufe von depthFirstSearch mit Ausnahme des ersten, denn am Knoten 0 wird festgestellt, dass der Nachbar 5 noch nicht markiert ist. Nachdem dieser schließlich markiert ist, endet das Verfahren. Bild 2c zeigt die Situation am Ende. Alle Knoten sind markiert.

Definition: Ein ungerichteter Graph G heißt zusammenhängend, wenn es von jedem Knoten u zu jedem anderen Knoten v mindestens einen Weg gibt.

Ein maximaler zusammenhängender Teilgraph eines ungerichteten Graphen G heißt Zusammenhangskomponente (connected component) von G.

Beispiel: Der Graph in Bild 2a ist zusammenhängend, der Graph in Bild 3a ist nicht zusammenhängend.

Wird das Verfahren der Tiefensuche auf einen nicht zusammenhängenden Graphen angewendet, so werden zunächst nur diejenigen Knoten markiert, die vom Startknoten aus erreichbar sind. Diese Knoten bilden eine Zusammenhangskomponente des Graphen. Unter den restlichen Knoten, die noch nicht markiert sind, wird dann ein neuer Startknoten gewählt und das Verfahren erneut gestartet, sodass damit die nächste Zusammenhangskomponente gefunden wird usw.

Das folgende Verfahren findet alle Zusammenhangskomponenten eines ungerichteten Graphen. Zu Beginn werden alle Knoten des Graphen mit der Zahl 0 markiert, dies soll bedeuten, dass sie nicht markiert sind. Das Verfahren depthFirstSearch markiert nun jeden besuchten Knoten mit einer Komponentennummer c; diese wird bei jedem neuen Start der Tiefensuche um 1 erhöht.

Algorithmus connectedComponents

Eingabe:

Ungerichteter Graph G

Ausgabe:

Markierung der Knoten, die für jeden Knoten die Nummer seiner Zusammenhangskomponente angibt

Methode:

markiere alle Knoten mit 0
setze c = 0
für alle Knoten v wiederhole

wenn v mit 0 markiert ist dann

setze c = c + 1

depthFirstSearch(v)

Die für dieses Verfahren verwendete Funktion depthFirstSearch ist folgende:

Funktion depthFirstSearch(v)

Methode:

markiere den Knoten v mit der Zahl c
für alle Nachbarknoten w von v wiederhole

wenn w mit 0 markiert ist dann

depthFirstSearch(w)

Bild 3a zeigt einen nicht zusammenhängenden Graphen. Beim ersten Durchlauf mit dem Startknoten 0 erreicht depthFirstSearch die linke Zusammenhangskomponente des Graphen. Diese Knoten erhalten die Komponentennummer c = 1. Die Knoten der rechten Zusammenhangskomponente bleiben zunächst mit 0 markiert (Bild 3b). Beim erneuten Start von depthFirstSearch mit dem Startknoten 1 werden auch diese Knoten erreicht; sie erhalten die Komponentennummer c = 2 (Bild 3c).

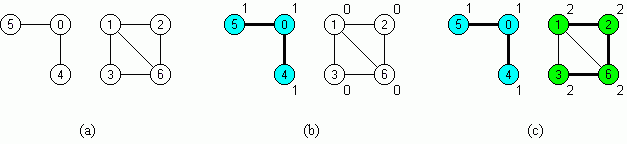
Bild 3: Berechnung der Zusammenhangskomponenten mit Hilfe von depthFirstSearch

Bild 3: Berechnung der Zusammenhangskomponenten mit Hilfe von depthFirstSearch

Im Algorithmus connectedComponents wird für jeden Knoten v des Graphen irgendwann einmal depthFirstSearch(v) aufgerufen, entweder auf oberster Ebene oder innerhalb der Rekursion. In depthFirstSearch(v) werden alle Nachbarknoten w von v durchlaufen; es werden also alle Kanten (v, w) betrachtet. Insgesamt wird somit jede Kante (v, w) des Graphen genau zweimal betrachtet, einmal vom Knoten v aus und einmal vom Knoten w aus. Für einen Graphen mit m Kanten ergibt sich hieraus ein Aufwand von Θ(m) Schritten. Der Aufwand, der für das Markieren der n Knoten des Graphen erforderlich ist, lässt sich im Aufwand für die Kanten unterbringen, vorausgesetzt, dass der Graph mindestens n Kanten hat. Es kann schließlich sein, dass der Graph nur aus isolierten Knoten besteht. Daher wird die Komplexität des Algorithmus connectedComponents mit Θ(n + m) angegeben. Je nach Anzahl der Kanten des Graphen liegt die Komplexität also zwischen Θ(n) und Θ(n²).

Das folgende Programm verwendet einen Marker, um die Elemente der Menge {0, ..., n-1}, entsprechend den Knoten des Graphen, zu markieren. Zum Durchlaufen aller Nachbarknoten eines Knotens wird ein NeighbourIterator verwendet. Iterator und ArrayList sind zuvor aus dem Package java.util zu importieren.

public class ConnectedComponents
{
    private Graph<?> graph;
    private Marker<Integer> marker;
    private int n, c;

    public ConnectedComponents(Graph<?> graph_)
    {
        graph=graph_;
        n=graph.getSize();
        marker=new Marker<Integer>(n, 0);
        computeComponents();
    }

    private void computeComponents()
    {
        c=0;
        // alle Knoten v des Graphen durchlaufen
        for (int v=0; v<n; v++)
            if (!marker.isMarked(v))
            {
                c=c+1;    // neue Zusammenhangskomponente gefunden
                depthFirstSearch(v);
            }
    }

    private void depthFirstSearch(int v)
    {
        marker.setMark(v, c);    // Knoten v mit der Komponentennummer c markieren

        // alle Nachbarn w des Knotens v durchlaufen
        int w;
        Iterator<Integer> it=graph.getNeighbourIterator(v);
        while (it.hasNext())
        {
            w=it.next();
            if (!marker.isMarked(w))
                depthFirstSearch(w);
        }
    }

    // liefert die Anzahl der Zusammenhangskomponenten des Graphen
    public int getNumberOfComponents()
    {
        return c;
    }

    // liefert alle Knoten der Zusammenhangskomponente i (i=1, 2, ...)
    public ArrayList<Integer> getComponent(int i)
    {
        ArrayList<Integer> a=new ArrayList<Integer>();
        for (int v=0; v<n; v++)
            if (marker.getMark(v)==i)
                a.add(v);
        return a;
    }

}    // end class ConnectedComponents

Die Berechnung der Zusammenhangskomponenten eines Graphen g lässt sich mit folgendem Programmstück aufrufen:

ConnectedComponents ccp=new ConnectedComponents(g);
// Ausgabe der Zusammenhangskomponenten
int k=ccp.getNumberOfComponents();
for (int i=1; i<=k; i++)
System.out.println(ccp.getComponent(i));

Weiter mit: [Zweifacher Zusammenhang] [Literatur] oder [up]

H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 17.09.2012 Updated: 20.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden

Graphenalgorithmen

Zusammenhangskomponenten eines Graphen

Tiefensuche

Zusammenhangskomponenten

Komplexität

Implementierung