Graphenalgorithmen

Graph als Datenstruktur

Gegeben ist ein gerichteter oder ungerichteter Graph G = (V, E) mit V = {0, ..., n-1}, n ∈ ℕ und E ⊆ V × V.

Als Beispiel zeigt Bild 1 einen Graphen G.

Bild 1: Graph G

Gesucht ist nach Möglichkeiten, einen solchen Graphen in Form einer geeigneten Datenstruktur darzustellen. Dabei soll die Datenstruktur so beschaffen sein, dass Graphenalgorithmen effizient darauf zugreifen können, z.B. dass sich alle Knoten, die zu einem bestimmten Knoten benachbart sind, effizient durchlaufen lassen.

Es stellt sich heraus, dass es schwierig ist, eine für alle Anwendungsfälle optimale Datenstruktur zu finden. Es gibt Graphen mit vielen Kanten oder wenigen Kanten, spezielle Graphen wie Gitter oder Bäume, gerichtete und ungerichtete Graphen, und später werden auch noch Graphen mit Kantenmarkierungen hinzukommen.

Daher werden wir die konkrete Implementierung als Datenstruktur zunächst offen lassen. Stattdessen fassen wir zunächst nur die als sicher geltenden Gemeinsamkeiten aller dieser konkreten Implementierungen in Form einer abstrakten Klasse Graph zusammen.

Ähnlich wie ein Interface legt eine abstrakte Klasse abstrakte Methoden fest, die in allen konkreten Klassen, die von der abstrakten Klasse abgeleitet sind, implementiert sein müssen. Eine abstrakte Klasse kann aber zusätzlich auch Attribute und bereits implementierte Methoden enthalten. Von einer abstrakten Klasse können keine Objekte angelegt werden, sondern nur von konkreten Klassen, die von der abstrakten Klasse abgeleitet sind. Die folgende abstrakte Klasse Graph dient als Grundgerüst für konkrete Klassen, mit denen sowohl gerichtete als auch ungerichtete Graphen sowie ferner Graphen mit Kantenmarkierungen modelliert werden.

Um diese Einheitlichkeit zu erzielen, stellen wir die Kantenmenge E eines Graphen G = (V, E) als Abbildung

w : V × V → T

dar, die jedem Knotenpaar (i, j) einen Wert aus einer Menge T zuweist. Hierbei wird ein spezieller Wert noedge ∈ T genau allen Knotenpaaren (i, j) ∉ E zugewiesen. Kanten und Nicht-Kanten sind also mit Werten aus T markiert, und Nicht-Kanten sind daran zu erkennen, dass sie mit dem speziellen Wert noedge markiert sind. In der Implementierung wird die Menge T der Klasse als Typ-Parameter Type übergeben.

Bei einem Graphen ohne Kantenmarkierungen ist T = {false, true} = Boolean. Der spezielle Wert noedge, mit dem Nicht-Kanten markiert werden, ist gleich false. Umgekehrt bedeutet w(u, v) = true, dass (i, j) eine Kante ist. Bei einem Graphen ohne Kantenmarkierungen sind also alle Kanten mit true markiert.

Bei einem Graphen mit Kantenmarkierungen ist beispielsweise T = Double, alle Nicht-Kanten (i, j) sind mit noedge = ∞ markiert, und bei allen Kanten entspricht w(i, j) der jeweiligen Markierung der Kante. Kantenmarkierungen, die reelle Zahlen sind, werden auch als Kantengewichte bezeichnet.

Es folgt die abstrakte Klasse Graph.

import java.util.Iterator;

public abstract class Graph<Type>
{
    protected int n;

    public Graph(int n_)
    {
        n=n_;
    }

    // gibt die Anzahl der Knoten zurück
    public int getSize()
    {
        return n;
    }

    // löscht alle Kanten
    protected void initialize()
    {
        for (int i=0; i<n; i++)
            for (int j=0; j<n; j++)
                deleteEdge(i, j);
    }

    // true, wenn (i, j) eine Kante ist
    public boolean isEdge(int i, int j)
    {
        return !getWeight(i, j).equals(noEdge());
    }

    // löscht die Kante (i, j)
    public void deleteEdge(int i, int j)
    {
        setWeight(i, j, noEdge());
    }

    // liefert den speziellen Wert noedge, mit dem Nicht-Kanten markiert sind
    public abstract Type noEdge();

    // liefert die Markierung w(i, j)
    public abstract Type getWeight(int i, int j);

    // setzt w(i, j)=w
    public abstract void setWeight(int i, int j, Type w);

    // iteriert über alle Nachbarn des Knotens i
    public abstract Iterator<Integer> getNeighbourIterator(int i);

}    // end class Graph

Die abstrakte Methode noEdge() ist dafür vorgesehen, den speziellen Wert noedge je nach konkreter Implementierung zu liefern. Die Methode isEdge(i, j) ergibt true, wenn (i, j) nicht mit noedge markiert ist, also eine Kante ist. Mit deleteEdge(i, j) wird der Kante (i, j) die Markierung noedge zugewiesen, hierdurch wird sie gelöscht. Die abstrakten Methoden setWeight und getWeight sind dazu gedacht, einem Paar von Knoten (i, j) die Markierung (das "Gewicht") w(i, j) zuzuweisen bzw. es abzurufen.

Für das Durchlaufen aller derjenigen Knoten, zu denen von einem bestimmten Knoten aus eine Kante hinführt, wird ein Iterator verwendet. Die Methode getNeighbourIterator gibt einen solchen Iterator zurück. Je nach Implementierung des Graphen unterscheidet sich auch die Implementierung dieses Iterators und die Effizienz des Iterierens.

Eine einfache Möglichkeit zur konkreten Implementierung eines Graphen besteht darin, die Kanten des Graphen in Form einer Adjazenzmatrix darzustellen.

Definition: Sei G = (V, E) ein Graph mit V = {0, ..., n-1}, n ∈ ℕ. Die Adjazenzmatrix des Graphen ist eine boolesche n × n-Matrix A, für die gilt

A_i,j =

`true`	falls (`i`, `j`) eine Kante ist, d.h. falls (`i`, `j`) ∈ `E`
`false`	sonst

für alle i, j ∈ V.

Beispiel: Der Graph aus Bild 1 lässt sich durch folgende Adjazenzmatrix darstellen (leere Einträge = false, 1 = true):

	0	1	2
0		1	1
1			1
2	1
3	1
4

Graphen mit Kantenmarkierungen aus einer Menge T lassen sich ebenfalls in Form einer Matrix speichern. Hierbei wird für jede Kante (i, j) die Kantenmarkierung w(i, j) an Position (i, j) der Matrix gespeichert. Für alle Nicht-Kanten (i, j) wird der Wert noedge an Position (i, j) der Matrix gespeichert.

Abstrakte Klasse GraphMatrixRepresentation

Es folgt eine entsprechende Implementierung der wiederum noch abstrakten Klasse GraphMatrixRepresentation, die von der abstrakten Klasse Graph abgeleitet ist. Die Menge T für die Kantenmarkierungen wird der Klasse als Typ-Parameter Type übergeben.

Wir speichern die Matrix nicht als Array, da es in Java nicht möglich ist, Arrays mit Einträgen eines unbestimmten Typ-Parameters Type zu erzeugen. Stattdessen speichern wir die Matrix als ArrayList von Zeilen, wobei die Zeilen wiederum ArrayLists mit Einträgen eines zunächst unbestimmten Typs Type sind.

import java.util.ArrayList;
import java.util.Iterator;

public abstract class GraphMatrixRepresentation<Type> extends Graph<Type>
{
    private ArrayList<ArrayList<Type>> a;

    public GraphMatrixRepresentation(int n_)
    {
        super(n_);
        // Darstellung der Matrix als ArrayList von ArrayLists
        a=new ArrayList<ArrayList<Type>>();
        for (int i=0; i<n; i++)
        {
            a.add(new ArrayList<Type>());
            for (int j=0; j<n; j++)
                a.get(i).add(noEdge());
        }
    }

    @Override
    public Type getWeight(int i, int j)
    {
        return a.get(i).get(j);
    }

    @Override
    public void setWeight(int i, int j, Type b)
    {
        a.get(i).set(j, b);
    }

    @Override
    public Iterator<Integer> getNeighbourIterator(int i)
    {
        return new NeighbourIterator(this, i);
    }

}

Eine Implementierung des Iterators NeighbourIterator findet sich weiter unten.

Gerichtete Graphen

Nach so vielen Vorarbeiten sind wir nun in der Lage, die konkreten Klassen DirectedGraph für gerichtete Graphen und WeightedDirectedGraph für gerichtete Graphen mit Kantengewichten anzugeben. Es sind jeweils nur noch der konkrete Typ-Parameter und der zugehörige Wert noedge anzugeben. Darauf folgend werden wir entsprechende Klassen für ungerichtete Graphen angeben.

Das folgende Bild 2 zeigt das Klassendiagramm der betreffenden Klassen.

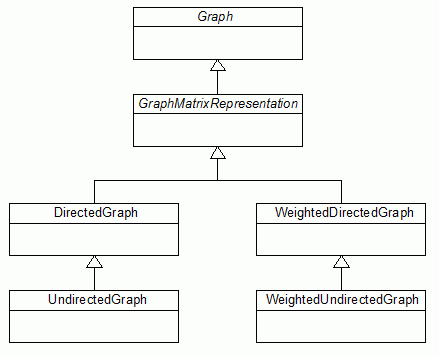
Bild 2: Klassendiagramm der Implementierung von Graphen

public class DirectedGraph extends GraphMatrixRepresentation<Boolean>
{
    public DirectedGraph(int n_)
    {
        super(n_);
    }

    @Override
    public Boolean noEdge()
    {
        return false;
    }

}

Für gerichtete Graphen mit Kantengewichten vom Typ Double ergibt sich folgende Klasse WeightedDirectedGraph.

public class WeightedDirectedGraph extends GraphMatrixRepresentation<Double>
{
    public WeightedDirectedGraph(int n_)
    {
        super(n_);
    }

    @Override
    public Double noEdge()
    {
        return Double.POSITIVE_INFINITY;
    }

}

Ungerichtete Graphen

Ein ungerichteter Graph lässt sich als gerichteter Graph ansehen, dessen Kantenrelation symmetrisch ist, also als Spezialfall eines gerichteten Graphen. Entsprechend modellieren wir ungerichtete Graphen, indem wir die Klasse UndirectedGraph von DirectedGraph ableiten und nur die Methode setWeight in der Weise überschreiben, dass mit jeder Kante (i, j) auch die Kante (j, i) erzeugt wird.

public class UndirectedGraph extends DirectedGraph
{
    public UndirectedGraph(int n_)
    {
        super(n_);
    }

    @Override
    public void setWeight(int i, int j, Boolean w)
    {
        // Kanten in beiden Richtungen erzeugen
        super.setWeight(i, j, w);
        super.setWeight(j, i, w);
    }

}

In entsprechender Weise wird die Klasse WeightedUndirectedGraph von der Klasse WeightedDirectedGraph abgeleitet.

public class WeightedUndirectedGraph extends WeightedDirectedGraph
{
    public WeightedUndirectedGraph(int n_)
    {
        super(n_);
    }

    @Override
    public void setWeight(int i, int j, Double w)
    {
        // Kanten in beiden Richtungen erzeugen
        super.setWeight(i, j, w);
        super.setWeight(j, i, w);
    }

}

Iterator NeighbourIterator

Zum Durchlaufen aller Nachbarknoten eines bestimmten Knotens verwenden wir einen Iterator.

Die Implementierung des Iterators NeighbourIterator berücksichtigt, dass ein Knoten möglicherweise gar keinen Nachbarknoten hat. Daher wird im Konstruktor zunächst die Methode tryNext aufgerufen. Die Methode tryNext sucht den ersten Nachbarknoten j; falls dieser nicht existiert, wird j bis zum Wert getSize() erhöht und die Methode getNext liefert gleich zu Beginn false.

Eine andere Möglichkeit besteht darin, den NeighbourIterator als FilterIterator zu implementieren.

import java.util.Iterator;

public class NeighbourIterator implements Iterator<Integer>
{
    private Graph<?> g;
    private int i, j;

    public NeighbourIterator(Graph<?> g_, int i_)
    {
        g=g_;
        i=i_;
        j=-1;
        tryNext();
    }

    @Override
    public boolean hasNext()
    {
        return j<g.getSize();
    }

    @Override
    public Integer next()
    {
        int k=j;
        tryNext();
        return k;
    }

    private void tryNext()
    {
        j++;
        while (j<g.getSize())
            if (g.isEdge(i, j))
                return;
            else
                j++;
    }

    @Override
    public void remove()
    {
        // not implemented
    }

}

Eine Adjazenzliste ist eine Liste aller Knoten, zu denen von einem bestimmten Knoten aus eine Kante hinführt. Um einen Graphen (ohne Kantenmarkierungen) darzustellen, wird also für jeden seiner Knoten eine Adjazenzliste benötigt.

Beispiel: Der Graph G aus Bild 1 lässt sich durch folgende Adjazenzlisten seiner Knoten 0, ..., 4 darstellen:

0	1	2
1	2
2	0
3	0
4

Aus dieser Darstellung geht hervor, dass vom Knoten 0 aus Kanten zu den Knoten 1 und 2 hinführen, vom Knoten 1 aus eine Kante zum Knoten 2, vom Knoten 2 zum Knoten 0 usw.

Es bietet sich an, die Adjazenzlisten als ArrayList zu implementieren. Als Neighbour\-Iterator kann dann der Standard-Iterator des Typs ArrayList verwendet werden.

Aufgabe 1: Programmieren Sie eine entsprechende Implementierung eines Graphen ohne Kantenmarkierungen als abstrakte Klasse GraphListRepresentation, abgeleitet von der abstrakten Klasse Graph mit Typ-Parameter Boolean. Stellen Sie die Adjazenzlisten durch Objekte vom Typ ArrayList mit Typ-Parameter Integer dar. Implementieren Sie die abstrakten Methoden der abstrakten Klasse Graph.

Weiter mit: [Zusammenhangskomponenten] oder [up]

H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 08.02.2012 Updated: 20.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden

Graphenalgorithmen

Graph als Datenstruktur

Abstrakte Klasse Graph

Implementierung mit Adjazenzmatrix

Abstrakte Klasse GraphMatrixRepresentation

Gerichtete Graphen

Ungerichtete Graphen

Iterator NeighbourIterator

Implementierung mit Adjazenzlisten