Graphenalgorithmen
Zweifacher Zusammenhang
Ein ungerichteter Graph heißt zusammenhängend, wenn es von jedem Knoten zu jedem anderen Knoten mindestens einen Weg gibt. In ähnlicher Weise lässt sich der zweifache Zusammenhang charakterisieren. Ein ungerichteter Graph heißt zweifach zusammenhängend, wenn es von jedem Knoten zu jedem anderen Knoten mindestens zwei disjunkte Wege gibt, also Wege, die außer Anfangs- und Endknoten keine Knoten gemeinsam haben.
Ist ein ungerichteter Graph nicht zusammenhängend, so besteht er aus mehreren Zusammenhangskomponenten, also Teilgraphen, die jeweils für sich zusammenhängend sind und die zusammengenommen den ganzen Graphen ergeben. Ist der Graph nicht zweifach zusammenhängend, so besteht er ganz entsprechend aus mehreren Zweifach-Zusammenhangskomponenten oder Blöcken.
Wie die (einfachen) Zusammenhangskomponenten lassen sich auch die Zweifach-Zusammenhangskomponenten mit Hilfe der Tiefensuche berechnen.
Tiefensuche
Gegeben ist ein nichtleerer zusammenhängender ungerichteter Graph. Mit Hilfe der Tiefensuche (depth-first search) lässt sich der Graph systematisch durchlaufen. In dieser Version der Tiefensuche werden die Knoten entsprechend der Reihenfolge nummeriert, in der sie durchlaufen werden.
Zu Beginn werden alle Knoten des Graphen G mit der Zahl 0 markiert und es wird ein Startknoten v gewählt. Die globale Zählvariable i wird mit 0 initialisiert.
Funktion depthFirstSearch(v)
Methode:
- setze i = i+1
- markiere den Knoten v mit der Nummer i
- für alle Nachbarknoten w von v wiederhole
- wenn w mit 0 markiert ist dann
- depthFirstSearch(w)
Die Markierung i, die ein Knoten v im Verlauf des Verfahrens erhält, wird als der Tiefensuchindex (depth-first index) dfi(v) bezeichnet.
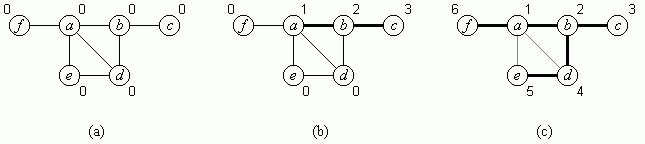
Bild 1: Tiefensuche in einem Graphen
Bild 1a zeigt als Beispiel einen Graphen mit Knotenmenge { a, ..., f }. Zu Beginn sind alle Knoten mit 0 markiert. Als Startknoten wird der Knoten a gewählt; dieser wird mit dem Tiefensuchindex i = 1 markiert. Mit dem Nachbarn b wird fortgefahren; dieser erhält die Markierung i = 2. Werden nun die Nachbarn von b betrachtet, so hat a bereits eine Markierung > 0, also wird mit dem nächsten Nachbarn c fortgefahren; dieser erhält die Markierung i = 3. Bild 1b zeigt diese Situation. Die Kanten, die zu den jeweils neu markierten Knoten führen, sind fett gezeichnet.
Im weiteren Verlauf des Verfahrens wird festgestellt, dass Knoten c keine Nachbarn hat, die mit 0 markiert sind. Der entsprechende Aufruf von depthFirstSearch ist daher hier abgeschlossen und es wird mit dem nächsten Nachbarn des Knotens b fortgefahren, also mit Knoten d.
Vom Knoten e schließlich ist wiederum kein Knoten mehr erreichbar, der mit 0 markiert ist. Hier enden nun alle rekursiven Aufrufe von depthFirstSearch mit Ausnahme des ersten, denn am Knoten a wird festgestellt, dass der Nachbar f noch mit 0 markiert ist. Nachdem dieser mit dem Tiefensuchindex i = 6 markiert ist, endet das Verfahren. Bild 1c zeigt die Situation am Ende. Alle Knoten sind mit einem Tiefensuchindex > 0 markiert.
Tiefensuchbaum
Die Kanten eines ungerichteten Graphen sind nichts anderes als jeweils zwei gerichtete Kanten, die in entgegengesetzte Richtungen zeigen. Unter dieser Sichtweise bilden die Knoten des Graphen zusammen mit den Kanten, die im Verlauf der Tiefensuche zu den jeweils neu markierten Knoten führen, einen gerichteten Baum mit dem Startknoten als Wurzel. Dieser Baum wird als Tiefensuchbaum D des Graphen bezeichnet. Die Kanten des Graphen, die zu diesem Tiefensuchbaum gehören, heißen daher in diesem Zusammenhang Baumkanten. Die Baumkanten sind immer vom Knoten mit dem kleineren zum Knoten mit dem größeren Tiefensuchindex gerichtet. Die entsprechenden entgegengesetzt gerichteten Kanten nennen wir reverse Baumkanten. Die verbleibenden Kanten des Graphen heißen Vorwärts- bzw. Rückwärtskanten, je nach dem, ob sie in Richtung vom kleineren zum größeren Tiefensuchindex führen oder umgekehrt. Ein Teilbaum des Tiefensuchbaums, der an einem Knoten v beginnt, wird mit D(v) bezeichnet.
Bild 2 zeigt einen Ausschnitt aus Bild 1c mit einer Baumkante, einer reversen Baumkante, einer Vorwärts- und einer Rückwärtskante.
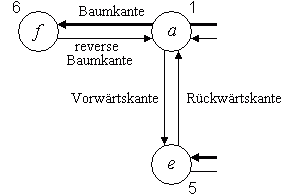
Bild 2: Baumkante, reverse Baumkante, Vorwärts- und Rückwärtskante
Behauptung: Jede von einem Knoten v ausgehende Vorwärtskante führt zu einem Nachfolger w von v im Tiefensuchbaum D, d.h.
(v, w) ist Vorwärtskante ⇒ w ist Nachfolger von v in D.
Es ist also nicht möglich, dass eine Vorwärtskante quer im Tiefensuchbaum verläuft, wie in Bild 3 angedeutet; eine solche Kante gibt es bei einem Tiefensuchbaum nicht.
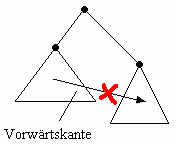
Bild 3: Eine Vorwärtskante verläuft nie quer zum Tiefensuchbaum
Beweis: Angenommen (v, w) sei Vorwärtskante, d.h. dfi(v) < dfi(w), und w liege nicht im Teilbaum D(v) der von v aus erreichbaren Knoten. Dann wird w erst markiert, nachdem alle von v aus erreichbaren Knoten markiert sind. Dies aber ist ein Widerspruch, denn w selbst ist (sogar direkt) von v aus erreichbar.
Die Folgerung ist, dass jede Rückwärtskante zu einem Vorgänger im Tiefensuchbaum führt.
Zweifach zusammenhängende Komponenten (Blöcke)
Definition: Ein ungerichteter Graph G heißt zweifach zusammenhängend, wenn es in G von jedem Knoten zu jedem anderen Knoten mindestens zwei disjunkte Wege gibt, also Wege, die außer Anfangs- und Endknoten keine Knoten gemeinsam haben.
Ein maximaler zweifach zusammenhängender Teilgraph eines Graphen G heißt Zweifach-Zusammenhangskomponente (biconnected component) oder Block (block) von G.
Ein Graph, der nur aus einem Knoten besteht, ist zweifach zusammenhängend, denn er hat keine anderen Knoten. Ein Graph mit zwei Knoten u und v, die durch eine Kante verbunden sind, ist ebenfalls zweifach zusammenhängend. Denn es gibt die beiden Wege (u, v) und (u, v). Diese sind zwar gleich, aber dennoch disjunkt, denn sie enthalten außer Anfangs- und Endknoten keine gemeinsamen Knoten.
Wird aus einem zusammenhängenden ungerichteten Graphen ein Knoten v entfernt (mitsamt seiner Kanten), so gibt es zwei Möglichkeiten: Entweder bleibt der Graph zusammenhängend, oder er zerfällt in mehrere Zusammenhangskomponenten. Ein solcher Knoten v, der den Graphen zerfallen lässt, wenn er entfernt wird, heißt Zerfällungsknoten (cut point).1)
Satz: Ein zusammenhängender ungerichteter Graph G ist genau dann zweifach zusammenhängend, wenn er keine Zerfällungsknoten hat.
Bild 4 zeigt einen zusammenhängenden ungerichteten Graphen. Der Knoten c in der Mitte ist ein Zerfällungsknoten.
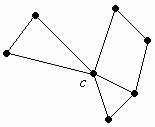
Bild 4: Zusammenhängender ungerichteter Graph mit Zerfällungsknoten c
Die Blöcke und Zerfällungsknoten eines Graphen lassen sich mithilfe der Tiefensuche bestimmen.
Wir nennen einen Knoten v einen Anführer eines Blocks (block leader), wenn v im Tiefensuchbaum einen direkten Nachfolger w hat, von dessen Teilbaum D(w) keine Rückwärtskante zu einem Vorgänger u von v führt. Die Knoten von D(w) können dann von anderen Knoten aus nur über den Knoten v erreicht werden. Wenn D(w) keine Anführer von weiteren Blöcken enthält, bildet v zusammen mit den Knoten von D(w) einen Block.
Beispiel: Bild 5 zeigt eine Rückwärtskante von D(w) zu einem Vorgänger u von v. Wenn eine derartige Rückwärtskante nicht existiert, so ist v Anführer eines Blocks.
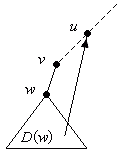
Bild 5: Rückwärtskante von D(w) zu einem Vorgänger u von v
Ein Knoten c ist ein Zerfällungsknoten, wenn er Anführer eines Blocks ist und außerdem noch zu einem anderen Block gehört. Stets ist der Startknoten Anführer eines Blocks. Er ist Zerfällungsknoten, wenn er außerdem noch Anführer eines anderen Blocks ist. In einem zweifach zusammenhängenden Graphen ist nur der Startknoten Anführer eines Blocks.
Implementierung
Der folgende Algorithmus bestimmt die Blöcke und Zerfällungsknoten eines zusammenhängenden, ungerichteten Graphen mithilfe der Tiefensuche [AHU 74].
Jedem Knoten v wird zusätzlich zum Tiefensuchindex dfi(v) ein Wert min(v) zugeordnet. Dieser Wert wird mit dfi(v) initialisiert. Er wird in zwei Fällen aktualisiert:
- wenn eine Rückwärtskante (v, w) gefunden wird; dann wird min(v) auf dfi(w) gesetzt, falls min(v) dadurch kleiner wird (Aufruf von updateMin am Ende des Else-Teils); 2)
- wenn eine reverse Baumkante (w, v) durchlaufen wird; dann wird min(v) auf min(w) gesetzt, falls min(v) dadurch kleiner wird (Aufruf von updateMin am Ende des If-Teils).
Somit ist min(v) der minimale Tiefensuchindex aller Vorgänger von v, mit denen v oder ein Nachfolger von v durch eine Rückwärtskante verbundenen sind.
Ein Knoten v wird als Anführer eines Blocks identifiziert, wenn er einen direkten Nachfolger w hat, für den min(w) größer oder gleich dfi(v) ist. Dies bedeutet nämlich, dass weder von w noch von einem Nachfolger von w eine Rückwärtskante zu einem Vorgänger von v führt.
Die folgende Funktion findBlocks hat dieselbe rekursive Struktur wie depthFirstSearch. Jedem Knoten v ist zusätzlich zum Tiefensuchindex dfi(v) der Wert min(v), der Vorgänger pre(v) im Tiefensuchbaum, sowie eine Liste der Nummern der Blöcke, denen v angehört, zugeordnet. Mit assignBlockNumber(v, bln) wird dem Knoten v die Blocknummer bln zugeordnet.
Mit einem NeighbourIterator werden die Nachbarn eines jeweiligen Knotens der Reihe nach durchlaufen.
Ferner wird ein globaler Stack stk verwendet, in dem die durchlaufenen Knoten des Tiefensuchbaums gespeichert werden. Wird ein Anführer eines Blocks gefunden, so befinden sich die Knoten des betreffenden Blocks als oberste im Stack; sie werden vom Stack entfernt und als zu dem Block gehörig gekennzeichnet.
Als Zerfällungsknoten werden am Ende diejenigen Knoten identifiziert, die mehreren Blöcken angehören.
{
dfn++; // Tiefensuchindex erhöhen
dfi[v]=dfn;
min[v]=dfn;
int w, w1;
Iterator<Integer> it=graph.getNeighbourIterator(v);
while (it.hasNext()) // alle Nachbarn von v durchlaufen
{
w=it.next();
if (notVisited(w)) // (v, w) ist neue Baumkante
{
stk.push(w); // Knoten auf den Stack legen
pre[w]=v; // w hat Vorgänger v
findBlocks(w);
if (min[w]>=dfi[v])
{
bln++; // Blocknummer erhöhen
// Blocknummer allen Knoten dieses Blocks zuweisen
stk.push(v); // v is cut point
do
{
w1=stk.pop();
assignBlockNumber(w1, bln);
}
while (w!=w1);
}
updateMin(v, min[w]);
}
else if (dfi[v]>=dfi[w]) // (v, w) ist keine Vorwärtskante
if (w!=pre[v]) // (v, w) ist keine reverse Baumkante
// (v, w) ist Rückwärtskante
updateMin(v, dfi[w]);
}
Der angegebene Algorithmus funktioniert nicht mit einem Graphen, der nur aus einem isolierten Knoten besteht. Da der Knoten keinen Nachbarn hat, wird diesem Knoten kein Block zugeordnet. Es ist eine zusätzliche Abfrage erforderlich, ob der Graph nur aus einem Knoten besteht.
Mit einer ähnlichen Vorgehensweise wie bei der Berechnung der Zusammenhangskomponenten lassen sich auch für beliebige, möglicherweise nicht zusammenhängende Graphen die Zerfällungsknoten und Blöcke ihrer Zusammenhangskomponenten bestimmen. Dies geschieht, indem die Tiefensuche gegebenenfalls mehrmals durchgeführt wird, beginnend jeweils bei einem Knoten, der noch mit dem Tiefensuchindex 0 markiert ist.
1) Weitere Bezeichnungen: trennender Knoten, Artikulation (=Gelenk)
2) Wenn (v, w) eine Vorwärtskante ist, hat updateMin(v, dfi(w)) keine Wirkung, da bereits min(v) ≤ dfi(v) < dfi(w) gilt.
Weiter mit: [Literatur] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 25.10.2006 Updated: 20.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden