Konvexe Hülle

Graham-Scan-Algorithmus

Gesucht ist die konvexe Hülle einer endlichen Menge von Punkten in der Ebene. Die Idee des Verfahrens von Graham [Gra 72] ist, aus der Punktemenge zunächst ein sternförmiges Polygon zu konstruieren und dieses anschließend in ein konvexes Polygon umzuformen.

Aus der Punktemenge (Bild 1a) wird zunächst der Punkt q mit minimaler y-Koordinate, bzw. bei mehreren Punkten mit minimaler y-Koordinate, von diesen der Punkt mit minimaler x-Koordinate gewählt. Ausgehend von q werden die Winkel zu allen anderen Punkten bestimmt (Bild 1b). Die Punkte werden nach diesem Winkel sortiert und zu einem Polygonzug verbunden. Es entsteht ein sternförmiges Polygon (Bild 1c).

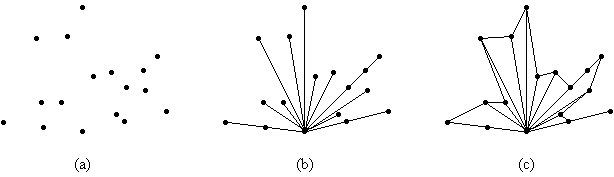
Bild 1: Aus der Punktemenge konstruierter sternförmiger Polygonzug

Es kann vorkommen, dass mehrere Punkte den gleichen Winkel haben (vgl. Bild 1b). Punkte gleichen Winkels werden zusätzlich absteigend nach ihrem Abstand zu q sortiert. Bei dem entstehenden Polygonzug können sich Kanten überlappen, sodass ein nicht einfacher Polygonzug entsteht. Dieser ist aber dennoch für den Algorithmus geeignet.

Der sternförmige Polygonzug wird nun ausgehend von q durchlaufen; dabei werden konkave Ecken überbrückt (siehe konvexe Hülle eines sternförmigen Polygons). Das Ergebnis ist ein konvexes Polygon, das die konvexe Hülle der Punktemenge darstellt.

Bild 2: Aus dem sternförmigen Polygonzug erzeugtes konvexes Polygon

In folgender Realisierung des Graham-Scan-Algorithmus wird die Tatsache ausgenutzt, dass aufgrund der Sortierung der Punkte die Ecken p₀ und p₁ konvex sind.

Algorithmus Graham-Scan

Eingabe:

Array p mit n Punkten

Ausgabe:

Array p derart umgeordnet, dass die ersten h Einträge die Ecken des konvexen Hüllpolygons sind

Methode:

bestimme Punkt q mit minimaler y-Koordinate
subtrahiere q von allen Punkten des Arrays (sodass q selbst zum Nullpunkt wird)
sortiere die Punkte des Arrays nach ihrem Winkel, und bei gleichem Winkel nach ihrem Abstand zum Nullpunkt (der Punkt q wird zu p₀)
addiere q zu allen Punkten des Arrays (sodass die ursprünglichen Punkte wiederhergestellt werden)
// durchlaufe die Punkte und überbrücke konkave Ecken:
setze i = 3 und k = 3
solange k < n wiederhole

vertausche p_i und p_k
solange p_i-2 p_i-1 p_i nicht konvex wiederhole

vertausche p_i-1 und p_i
setze i = i – 1

setze i = i + 1 und k = k + 1

setze h = i

Der Algorithmus hat die kleine Unschönheit, dass die letzte Ecke des berechneten konvexe Hüllpolygons eine 180°-Ecke sein kann (vgl. Bild 2). Wenn dies stört, ist es einfach, diese noch zu entfernen.

Um die Punkte nach ihrem Winkel zu sortieren, ist es nicht nötig, die Winkel tatsächlich zu berechnen. Der Sortieralgorithmus muss nur wissen, welcher von jeweils zwei Punkten p_i und p_j den größeren Winkel hat. Dies lässt sich danach entscheiden, ob das Dreieck 0 p_i p_j einen positiven oder negativen Flächeninhalt hat. Der doppelte Flächeninhalt ergibt sich durch die einfache Berechnung x_iy_j – x_jy_i (vgl. Fläche eines Dreiecks ). Bei gleichem Winkel, d.h. wenn die Dreiecksfläche gleich Null ist, werden die Punkte nach ihrem Abstand zum Nullpunkt sortiert. Es genügt hier, mit dem Manhattan-Abstand |x| + |y| zu rechnen.

Die Methode isLess der Klasse Point implementiert einen solchen Vergleich. Sie wird in der Sortierfunktion des Graham-Scan-Algorithmus benutzt.

Die folgende Klasse GrahamScan implementiert den Graham-Scan-Algorithmus. Der Aufruf erfolgt mit

GrahamScan c=new GrahamScan();
h=c.computeHull(p);

Hierbei ist p ein Array von Punkten. Als Ergebnis der Berechnung werden die Punkte im Array so umgeordnet, dass die ersten h Punkte die Ecken des konvexen Hüllpolynoms in umlaufender Reihenfolge bilden.

Die weiteren Funktionen sind Hilfsfunktionen. Die Funktion exchange(i, j) vertauscht zwei Punkte im Array. Die Funktion makeRelTo(p0) rechnet alle Punkte des Arrays relativ zu p₀ als Nullpunkt um. Die Funktion indexOfLowestPoint() sucht den Punkt mit kleinster y-Koordinate, oder bei mehreren Punkten mit kleinster y-Koordinate, von diesen den Punkt mit kleinster x-Koordinate. Als Ergebnis wird die Position des Punktes im Array zurückgegeben. Die Funktion isConvex(i) testet, ob die Punkte p_i-1 p_i p_i+1 eine konvexe Ecke eines Polygonzuges darstellen. Für das Sortieren der Punkte wird Quicksort verwendet.

public class GrahamScan
{
    private Point[] p;
    private int n;
    private int h;

    public int computeHull(Point[] p)
    {
        this.p=p;
        n=p.length;
        if (n<3) return n;
        h=0;
        grahamScan();
        return h;
    }

    private void grahamScan()
    {
        exchange(0, indexOfLowestPoint());
        Point pl=new Point(p[0]);
        makeRelTo(pl);
        sort();
        makeRelTo(pl.reversed());
        int i=3, k=3;
        while (k<n)
        {
            exchange(i, k);
            while (!isConvex(i-1))
                exchange(i-1, i--);
            k++;
            i++;
        }
        h=i;
    }

    private void exchange(int i, int j)
    {
        Point t=p[i];
        p[i]=p[j];
        p[j]=t;
    }

    private void makeRelTo(Point p0)
    {
        int i;
        Point p1=new Point(p0); // notwendig, weil p0 in p[] sein kann
        for (i=0; i<n; i++)
            p[i].makeRelTo(p1);
    }

    private int indexOfLowestPoint()
    {
        int i, min=0;
        for (i=1; i<n; i++)
            if (p[i].y<p[min].y || p[i].y==p[min].y && p[i].x<p[min].x)
                min=i;
        return min;
    }

    private boolean isConvex(int i)
    {
        return p[i].isConvex(p[i-1], p[i+1]);
    }

    private void sort()
    {
        quicksort(1, n-1); // ohne Punkt 0
    }

    private void quicksort(int lo, int hi)
    {
        int i=lo, j=hi;
        Point q=p[(lo+hi)/2];
        while (i<=j)
        {
            while (p[i].isLess(q)) i++;
            while (q.isLess(p[j])) j--;
            if (i<=j) exchange(i++, j--);
        }
        if (lo<j) quicksort(lo, j);
        if (i<hi) quicksort(i, hi);
    }

}   // end class GrahamScan

[CLRS 01] T.H. Cormen, C.E. Leiserson, R.L. Rivest, C. Stein: Introduction to Algorithms. 2. Auflage, The MIT Press (2001)

[Gra 72] R.L. Graham: An Efficient Algorithm for Determining the Convex Hull of a Finite Planar Set. Information Processing Letters 1, 132-133 (1972)

[PSh 85] F.P. Preparata, M.I. Shamos: Computational Geometry. Springer (1985)

[Web 1] http://www.cse.unsw.edu.au/~lambert/java/3d/hull.html

Weiter mit: [Jarvis-March-Algorithmus] oder [up]

H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 12.05.2003 Updated: 08.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden

Konvexe Hülle

Graham-Scan-Algorithmus

Idee

Verfahren

Sortieren der Punkte

Implementierung

Literatur