Konvexe Hülle
Jarvis-March-Algorithmus
Idee
Beim Verfahren von Jarvis [Jar 73] zur Berechnung der konvexen Hülle wird die Menge der Punkte in der Ebene wie mit einer Schnur umwickelt. Begonnen wird bei einem Punkt, der mit Sicherheit auf dem Rand der konvexen Hülle liegt, also z.B. mit einem Punkt mit minimaler y-Koordinate. Von dort aus wird der "am weitesten rechts liegende" Punkt gesucht; dies ist ein Punkt mit folgender Eigenschaft: Alle Punkte liegen links von der Verbindungsgeraden zu diesem Punkt oder auf der Verbindungsgeraden zu diesem Punkt. Von dort aus wird wiederum der nächste Punkt mit dieser Eigenschaft gesucht usw. Gibt es mehrere Punkte mit dieser Eigenschaft, so wird der am weitesten entfernte Punkt gewählt.
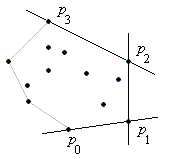
Bild 1: Folge gefundener Ecken beim Jarvis-March-Algorithmus
Das Verfahren endet, wenn der Ausgangspunkt wieder erreicht ist. Bild 1 zeigt, wie der Polygonzug, der den Rand der konvexen Hülle bildet, auf diese Weise erzeugt wird.
Implementierung
Die folgende Klasse JarvisMarch implementiert den Jarvis-March-Algorithmus. Der Aufruf erfolgt mit
h=c.computeHull(p);
Hierbei ist p ein Array von Punkten der Klasse Point. Die Punkte des Arrays werden so umgeordnet, dass die ersten h Punkte die Ecken des konvexen Hüllpolygons in umlaufender Reihenfolge bilden.
In der Funktion jarvisMarch wird als erstes durch die Aufruf von indexOfLowestPoint der Index eines Punktes mit minimaler y-Koordinate ermittelt. Dieser Punkt ist bereits eine Ecke der konvexen Hülle. Die Anzahl h der Ecken bleibt jedoch zunächst auf dem Anfangswert 0.
Anschließend werden folgende Schritte in einer Schleife wiederholt:
- die zuletzt gefundene Ecke der konvexen Hülle wird an die Position h im Array gebracht;
- von dieser Ecke aus wird der am weitesten rechts liegende Punkt gesucht; dieser stellt die nächste Ecke dar;
- die Anzahl h der Ecken wird um 1 erhöht.
Die Schleife bricht ab, wenn die Anfangsecke wieder erreicht ist, also der am Anfang gefundene Punkt mit minimaler y-Koordinate, der an Position 0 im Array steht. Die Variable h enthält nun die Anzahl der Ecken; die Arrayelemente 0, ..., h-1 sind die Ecken der konvexen Hülle in umlaufender Reihenfolge.
Die Funktion indexOfRightmostPointFrom verwendet die Funktion isLess aus der Klasse Point, die anhand des Flächeninhalts des Dreiecks q pi pj feststellt, welcher der Punkte pi und pj von q aus weiter rechts liegt.
{
private Point[] p;
private int n;
private int h;
public int computeHull(Point[] p)
{
this.p=p;
n=p.length;
h=0;
jarvisMarch();
return h;
}
private void jarvisMarch()
{
int i=indexOfLowestPoint();
do
{
exchange(h, i);
i=indexOfRightmostPointFrom(p[h]);
h++;
}
while (i>0);
}
private int indexOfLowestPoint()
{
int i, min=0;
for (i=1; i<n; i++)
if (p[i].y<p[min].y || p[i].y==p[min].y && p[i].x<p[min].x)
min=i;
return min;
}
private int indexOfRightmostPointFrom(Point q)
{
int i=0, j;
for (j=1; j<n; j++)
if (p[j].relTo(q).isLess(p[i].relTo(q)))
i=j;
return i;
}
private void exchange(int i, int j)
{
Point t=p[i];
p[i]=p[j];
p[j]=t;
}
} // end class JarvisMarch
Analyse
Die Bestimmung des Punktes mit minimaler y-Koordinate unter den n gegebenen Punkten dauert Zeit Θ(n). Die Schleife in der Funktion jarvisMarch wird h-mal durchlaufen, wobei h die Anzahl der Ecken des konvexen Hüllpolygons ist. Die Bestimmung des am weitesten rechts liegenden Punktes in jedem Aufruf von indexOfRightmostPointFrom dauert Zeit Θ(n).
Insgesamt ergibt dies eine Zeitkomplexität von Θ(n·h). Die Zeitkomplexität des Verfahrens hängt also davon ab, wie viele Ecken das konvexe Hüllpolygon am Ende hat. Dies können konstant viele sein, wenn etwa die konvexe Hülle ein Viereck ist. Im schlechtesten Fall aber kann das Hüllpolygon auch n Ecken haben, z.B. wenn die n Punkte auf einem Kreisumfang liegen. Die Komplexität liegt damit also zwischen Θ(n) und Θ(n2).
Literatur
[CLRS 01] T.H. Cormen, C.E. Leiserson, R.L. Rivest, C. Stein: Introduction to Algorithms. 2. Auflage, The MIT Press (2001)
[Jar 73] R.A. Jarvis: On the Identification of the Convex Hull of a Finite Set of Points in the Plane. Information Processing Letters 2, 18-22 (1973)
[PSh 85] F.P. Preparata, M.I. Shamos: Computational Geometry. Springer (1985)
[Web 1] http://www.cse.unsw.edu.au/~lambert/java/3d/hull.html
Weiter mit: [Quickhull-Algorithmus] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 19.01.2004 Updated: 08.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden