Konvexe Hülle

Polygon

Legt man ein Koordinatenkreuz in die Zeichenebene, so ist jeder Punkt der Zeichenebene durch seinen x- und y-Wert bestimmt. Wir können also die Punkte der Ebene mit Paaren von reellen Zahlen gleichsetzen. Die Menge der Punkte der Ebene ist dann die Menge ℝ². Die Menge ℝ² bildet einen Vektorraum über ℝ.

Definition: Ein Punkt in der Ebene ist ein Paar von reellen Zahlen, also ein Element p ∈ ℝ² mit p = (x, y).

Geometrische Objekte wie Linien und Flächen sind Mengen von Punkten. Diese Punkte lassen sich durch Vektoroperationen beschreiben.

Definition: Eine Gerade durch zwei Punkte p und q ist die Punktemenge

pq = { r ∈ ℝ² | r = p + a(q – p), a ∈ ℝ }.

Ein Liniensegment ist die Verbindungsstrecke von zwei Punkten p und q:

pq = { r ∈ ℝ² | r = p + a(q – p), a ∈ ℝ, 0 ≤ a ≤ 1 }.

Wir lassen den Querstrich über pq auch weg, wenn klar ist, dass das Liniensegment zwischen p und q gemeint ist.

Aus Liniensegmenten lassen sich weitere geometrische Gebilde zusammensetzen.

Definition: Ein Kantenzug ist eine Kette von Liniensegmenten

w = p₀p₁, p₁p₂, ..., p_n-1p_n.

Die Punkte p_i heißen Ecken des Kantenzugs, die Liniensegmente heißen Kanten.

Ein Polygonzug ist ein geschlossener Kantenzug

w = p₀p₁, p₁p₂, ..., p_n-1p₀.

Ein Polygonzug, bei dem alle Ecken p_i verschieden sind und bei dem je zwei Kanten außer den gemeinsamen Ecken keine Punkte gemeinsam haben, heißt einfacher Polygonzug.

Das von einem einfachen Polygonzug umschlossene Gebiet, einschließlich des Polygonzugs selber, heißt Polygon.

Beispiel: Bild 1 zeigt drei einfache Polygonzüge. Die Ecken sind durch dicke Punkte gekennzeichnet.

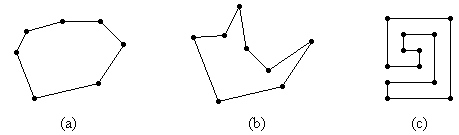
Bild 1: Einfache Polygonzüge

Gegeben sei ein einfacher Polygonzug p₀p₁, p₁p₂, ..., p_n-1p₀. Die Ecken p_i = (x_i, y_i) sind entgegen dem Uhrzeigersinn nummeriert, sodass die umschlossene Fläche stets links der Kanten p_ip_i+1 liegt (Bild 2).

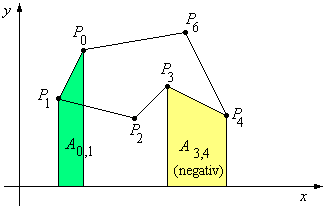
Bild 2: Flächen unter den Kanten eines Polygonzugs

Die Fläche des Trapezes unter der Kante p₀p₁ berechnet sich als

A_0,1 = (x₀ – x₁) (y₀ + y₁) / 2.

Entsprechend berechnen sich auch die Flächen unter den anderen Kanten. Im Beispiel von Bild 2 ergibt sich für A_3,4 eine negative Fläche, da x₃ < x₄ ist.

Addiert man alle Trapezflächen A_0,1, ..., A_n-1,0, so heben sich die unterhalb des Polygons liegenden positiven und negativen Flächen auf und es ergibt sich die von dem Polygonzug umschlossene Fläche A:

A = Summe _{i = 0, ..., n-1} A_i,i+1.

Hierbei wird i+1 modulo n gerechnet.

Die Flächenberechnung gestaltet sich besonders einfach, wenn sie auf ein Dreieck mit den Eckpunkten p₀, p₁, p₂ angewendet wird, dessen Eckpunkt p₀ im Nullpunkt liegt (Bild 3). Dann gilt für die doppelte Fläche F des Dreiecks ¹)

2F = x₁y₂ – x₂y₁.

Wichtig ist die Orientierung der Eckpunkte p₀, p₁ und p₂. Werden die Punkte in dieser Reihenfolge entgegen dem Uhrzeigersinn durchlaufen, ist die Dreiecksfläche positiv, im anderen Fall negativ.

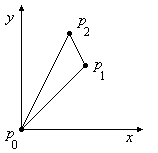
Bild 3: Dreieck mit p0 im Nullpunkt

Bild 3: Dreieck mit p₀ im Nullpunkt

Die Fläche eines beliebigen Dreiecks ergibt sich, indem die Punkte p₁ und p₂ relativ zu p₀ als Nullpunkt dargestellt werden und dann die obige Berechnung ausgeführt wird.

Definition: Eine Ecke p_i in einem Polygonzug p₀p₁, p₁p₂, ..., p_n-1p₀ heißt konvex, wenn für den links liegenden Winkel α zwischen den Kanten p_i-1p_i und p_ip_i+1 gilt 0° ≤ α < 180° (i-1 und i+1 werden modulo n gerechnet). Anderenfalls heißt die Ecke konkav.

Die in Bild 4a dargestellten Kanten eines Polygonzugs bilden eine konvexe Ecke, die in Bild 4b dargestellten Kanten bilden eine konkave Ecke.

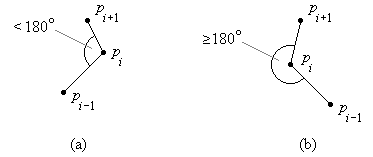
Bild 4: Konvexe Ecke eines Polygonzugs (a), konkave Ecke (b)

Um festzustellen, ob eine Ecke p_i eines Polygonzugs konvex oder konkav ist, berechnet man mit der oben angegebenen Methode die Fläche des Dreiecks p_i-1p_ip_i+1. Ergibt die Flächenberechnung eine positive Dreiecksfläche, so sind die Eckpunkte des Dreiecks entgegen dem Uhrzeigersinn nummeriert. In diesem Fall ist die Ecke konvex.

Wenn alle drei Punkte auf einer Geraden liegen, ist die Dreiecksfläche 0. Dann wird geprüft, ob die Ecke neben oder zwischen den beiden anderen Punkten liegt. Liegt sie neben den beiden anderen Punkten, ist der Winkel 0° und die Ecke damit konvex. Liegt sie zwischen den beiden anderen Punkten, ist der Winkel 180° und die Ecke damit konkav.

Ist der Flächeninhalt des Dreiecks negativ, so sind die Eckpunkte des Dreiecks im Uhrzeigersinn nummeriert und die Ecke ist somit konkav.

Die folgende Klasse Point modelliert einen Punkt in der Ebene. Die Klasse enthält bereits eine ganze Reihe von Methoden, die für die Berechnung der konvexen Hülle einer Menge von Punkten benötigt werden. Im Folgenden sei t der aktuelle Punkt this, mit dem die jeweiligen Methoden aufgerufen werden.

Die Funktion relTo(p) erzeugt einen neuen Punkt, der t relativ zum Punkt p als Nullpunkt darstellt. Die Funktion makeRelTo(p) transformiert t entsprechend. Die Funktionen moved(x0, y0) und reversed() erzeugen einen zu t verschobenen Punkt bzw. einen zu t am Nullpunkt gespiegelten Punkt.

Die Funktion isLower(p) gibt true zurück, wenn t eine kleinere y-Koordinate als p hat, oder, bei gleicher y-Koordinate, eine kleinere x-Koordinate.

Die Funktion isFurther(p) prüft, ob t weiter vom Nullpunkt entfernt liegt als p. Als Maß für die Entfernung vom Nullpunkt genügt hier der Manhattan-Abstand |x| + |y|. Die Funktion mdist() berechnet den Manhattan-Abstand von t zum Nullpunkt.

Die Funktion isBetween(p0, p1) prüft im Falle dass t, p₀ und p₁ auf einer Linie liegen, ob t zwischen p₀ und p₁ liegt.

Die Funktion cross(p) berechnet das Kreuzprodukt t × p; der Betrag dieses Wertes ist gleich dem doppelten Flächeninhalt des Dreiecks 0 t p. Diese Funktion wird als Hilfsfunktion mehrfach verwendet.

In der Funktion isLess(p) wird geprüft, ob der Ortsvektor von t einen kleineren Winkel zum Nullpunkt hat als der Ortsvektor eines Punktes p. Unter der Voraussetzung, dass beide Punkte oberhalb der x-Achse liegen, ist dies ist genau dann der Fall, wenn die Punkte 0, t, p entgegen dem Uhrzeigersinn durchlaufen werden, der Flächeninhalt des Dreiecks 0 t p also positiv ist. Die Funktion isLess(p) gibt in diesem Fall true zurück, und außerdem auch dann, wenn der Flächeninhalt 0 ist, aber t weiter vom Nullpunkt entfernt liegt als p.

Die Funktion area2(p0, p1) berechnet den doppelten Flächeninhalt des Dreiecks t p₀ p₁. Die Funktion area2(g) berechnet den doppelten Flächeninhalt eines Dreiecks, das durch die beiden Endpunkte g.p0 und g.p1 der Strecke g sowie den Punkt t gegeben ist. Ist der Flächeninhalt negativ, so liegt der Punkt t rechts von der Geraden g. Dies wird in der Funktion isRightOf(g) verwendet.

Die Funktion isConvex(p0, p1) prüft, ob die Ecke p₀ t p₁ konvex ist.

public class Point
{
    public double x, y;

    public Point(double x, double y)
    {
        this.x=x;
        this.y=y;
    }

    public Point(Point p)
    {
        this(p.x, p.y);
    }

    public Point relTo(Point p)
    {
        return new Point(x-p.x, y-p.y);
    }

    public void makeRelTo(Point p)
    {
        x-=p.x;
        y-=p.y;
    }

    public Point moved(double x0, double y0)
    {
        return new Point(x+x0, y+y0);
    }

    public Point reversed()
    {
        return new Point(-x, -y);
    }

    public boolean isLower(Point p)
    {
        return y<p.y || y==p.y && x<p.x;
    }

    public double mdist()   // Manhattan-Distanz
    {
        return Math.abs(x)+Math.abs(y);
    }

    public double mdist(Point p)
    {
        return relTo(p).mdist();
    }

    public boolean isFurther(Point p)
    {
        return mdist()>p.mdist();
    }

    public boolean isBetween(Point p0, Point p1)
    {
        return p0.mdist(p1)>=mdist(p0)+mdist(p1);
    }

    public double cross(Point p)
    {
        return x*p.y-p.x*y;
    }

    public boolean isLess(Point p)
    {
        double f=cross(p);
        return f>0 || f==0 && isFurther(p);
    }

    public double area2(Point p0, Point p1)
    {
        return p0.relTo(this).cross(p1.relTo(this));
    }

    public double area2(Line g)
    {
        return area2(g.p0, g.p1);
    }

    public boolean isRightOf(Line g)
    {
        return area2(g)<0;
    }

    public boolean isConvex(Point p0, Point p1)
    {
        double f=area2(p0, p1);
        return f<0 || f==0 && !isBetween(p0, p1);
    }

}    // end class Point

¹) Der Betrag von 2F entspricht dem Betrag des Vektorprodukts oder Kreuzprodukts der beiden Ortsvektoren p₁ und p₂.

Weiter mit: [Konvexe Hülle] oder [up]

H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 25.12.2002 Updated: 08.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden

Konvexe Hülle

Polygon

Grundlagen

Fläche eines Polygons

Fläche eines Dreiecks

Konvexe und konkave Ecken

Implementierung