Konvexe Hülle
Quickhull-Algorithmus
Idee
Der Quickhull-Algorithmus zur Berechnung der konvexen Hülle einer endlichen Menge von Punkten in der Ebene verwendet eine ähnliche Technik wie Quicksort: Teilmengen der Punkte werden jeweils partitioniert in diejenigen Punkte, die links von einer bestimmten Geraden liegen und diejenigen, die rechts der Geraden liegen. Diese Punktemengen werden dann rekursiv weiter behandelt.
Gegeben sei eine Gerade g durch zwei Ecken p0 und p1 des konvexen Hüllpolygons sowie die Menge R derjenigen Punkte, die rechts von g liegen (Bild 1).
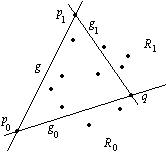
Bild 1: Situation bei der Ausführung des Quickhull-Algorithmus
In der Menge R wird der am weitesten von g entfernte Punkt q gesucht, dieser ist eine weitere Ecke des konvexen Hüllpolygons. Dann wird eine Gerade g0 durch p0 und q gelegt, und die Punktemenge R wird partitioniert in die Menge R0 derjenigen Punkte, die rechts von g0 liegen und die Menge L0 derjenigen Punkte, die links von g0 liegen.
Ferner wird eine Gerade g1 durch q und p1 gelegt, und L0 wird partitioniert in die Menge R1 derjenigen Punkte, die rechts von g1 liegen und die Menge L1 derjenigen Punkte, die links von g1 liegen.
Die Punkte der Menge L1 liegen im Inneren des konvexen Hüllpolygons. Mit den Geraden g0 und g1 und den zugehörigen Mengen R0 und R1 wird rekursiv weiter verfahren.
Um die Ausgangssituation herzustellen, wird der Punkt mit kleinster y-Koordinate bestimmt. Bei mehreren Punkten mit kleinster y-Koordinate wird von diesen der Punkt mit kleinster x-Koordinate gewählt. Dieser Punkt p0 ist eine Ecke des konvexen Hüllpolygons. Als zweite Ecke p1 wird ebenfalls p0 genommen. Damit die Abstandsberechnung durch Flächenberechnung mithilfe der Funktion area2 aus der Klasse Point funktioniert, wird p1 um ein sehr kleines Stück nach links verschoben.1) Durch p0 und p1 wird eine waagerechte Gerade g gelegt. Alle Punkte liegen somit rechts von g.
Implementierung
Die folgende Klasse QuickHull implementiert den QuickHull-Algorithmus. Der Aufruf erfolgt mit
h=c.computeHull(p);
Hierbei ist p ein Array von Punkten. Als Ergebnis der Berechnung werden die Punkte im Array so umgeordnet, dass die ersten h Punkte die Ecken des konvexen Hüllpolynoms in umlaufender Reihenfolge bilden.
In der Funktion quickhull wird zunächst der Punkt mit kleinster y-Koordinate gesucht und an die Position 0 im Array gebracht. Dann wird eine waagerechte Gerade durch die Punkte p0 und p0' erzeugt, wobei p0' durch Verschiebung von p0 nach links um ein sehr kleines Stück hervorgeht. Die rechts von der Geraden oder auf ihr liegenden Punkte (also alle Punkte), mit Ausnahme von p0, bilden den Anfangsbereich von Punkten, von dem die Ecken des Hüllpolygons berechnet werden. Die geschieht rekursiv mit der Funktion computeHullPoints(g, lo, hi).
Zunächst wird im Indexbereich von lo bis hi mit der Funktion indexOfFurthestPoint der am weitesten rechts von der Geraden liegende Punkt gesucht. Wiederum wird dies realisiert durch Berechnung des Flächeninhalts des Dreiecks, das aus den beiden gegebenen Punkten der Geraden und dem jeweils untersuchten Punkt pi gebildet wird. Alle Punkte pi liegen rechts von oder auf der Geraden, daher ist der Flächeninhalt stets 0 oder negativ. Da die Grundlinie des Dreiecks konstant bleibt, ist der negative Flächeninhalt ein Maß für die Höhe des Dreiecks, also für den Abstand des Punktes.
Wenn alle Punkte auf einer waagerechten Linie liegen und somit alle Flächeninhalte 0 sind, wird als der "am weitesten rechts von der Geraden" liegende Punkt der am weitesten rechts von p0 liegende Punkt genommen.
Von den beiden gegebenen Punkten der Geraden werden dann Verbindungsstrecken g0 und g1 zu dem entferntesten Punkt gezogen.
Die Funktion partition sortiert die Punkte des Arrays im Indexbereich zwischen lo und hi so, dass der Indexbereich zwischen lo und i-1 die Punkte enthält, die rechts von g liegen, und der Indexbereich zwischen i und hi die Punkte enthält, die links von oder auf g liegen. Als Rückgabewert liefert die Funktion die Position i.
Eine Besonderheit dieser Implementation besteht darin, dass die gefundenen Ecken des Hüllpolygons in der richtigen Reihenfolge an die Positionen 0, ..., h-1 des Arrays getauscht werden (so wie beim Graham-Scan- und beim Jarvis-March-Algorithmus). Dies geschieht durch jeweils drei Aufrufe der Funktion exchange.
{
private Point[] p;
private int n;
private int h;
private final static double eps=1e-3;
public int computeHull(Point[] p_)
{
p=p_;
n=p.length;
h=0;
quickHull();
return h;
}
private void quickHull()
{
exchange(0, indexOfLowestPoint());
h++;
Line g=new Line(p[0], p[0].moved(-eps,0));
computeHullPoints(g, 1, n-1);
}
private void computeHullPoints(Line g, int lo, int hi)
{
if (lo>hi) return;
int k=indexOfFurthestPoint(g, lo, hi);
Line g0=new Line(g.p0, p[k]);
Line g1=new Line(p[k], g.p1);
exchange(k, hi);
int i=partition(g0, lo, hi-1);
// alle Punkte von lo bis i-1 liegen rechts von g0
// alle Punkte von i bis hi-1 liegen links von g0
computeHullPoints(g0, lo, i-1);
// alle eben rekursiv erzeugten Punkte liegen
// auf dem Hüllpolygonzug vor p[hi]
exchange(hi, i);
exchange(i, h);
h++;
int j=partition(g1, i+1, hi);
// alle Punkte von i+1 bis j-1 liegen rechts von g1,
// alle Punkte von j bis hi liegen im Inneren
computeHullPoints(g1, i+1, j-1);
}
private int indexOfLowestPoint()
{
int i, min=0;
for (i=1; i<n; i++)
if (p[i].y<p[min].y || p[i].y==p[min].y && p[i].x<p[min].x)
min=i;
return min;
}
private void exchange(int i, int j)
{
Point t=p[i];
p[i]=p[j];
p[j]=t;
}
private int indexOfFurthestPoint(Line g, int lo, int hi)
{
int i, f=lo;
double d, mx=0;
for (i=lo; i<=hi; i++)
{
d=-p[i].area2(g);
if (d>mx || d==mx && p[i].x>p[f].x)
{
mx=d;
f=i;
}
}
return f;
}
private int partition(Line g, int lo, int hi)
{
int i=lo, j=hi;
while (i<=j)
{
while (i<=j && p[i].isRightOf(g)) i++;
while (i<=j && !p[j].isRightOf(g)) j--;
if (i<=j)
exchange(i++, j--);
}
return i;
}
} // end class QuickHull
Analyse
Die Analyse der Zeitkomplexität des Quickhull-Algorithmus gestaltet sich ähnlich wie bei Quicksort. Im besten Fall werden in jedem Rekursionsschritt (außer dem ersten) immer mindestens so viele Punkte ins Innere des bis dahin erzeugten Polygons verbannt, wie noch außerhalb verbleiben. Dann liegt die Komplexität in Θ(n log(n)). Im schlechtesten Fall besteht R0 in jedem Rekursionsschritt jeweils aus allen Punkten von R außer dem entferntesten Punkt q. Dann beträgt die Komplexität Θ(n2). Im Durchschnitt liegt die Komplexität in Θ(n log(n)).
Literatur
[PSh 85] F.P. Preparata, M.I. Shamos: Computational Geometry. Springer (1985)
[Web 1] http://www.cs.yorku.ca/~aaw/Hang/quick_hull/QuickHull.html
1) Ein – zugegeben – etwas unsauberer Trick.
Weiter mit: [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 12.02.2004 Updated: 08.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden