Theoretische Informatik
Konstruktion eines deterministischen endlichen Automaten
aus einem nichtdeterministischen endlichen Automaten
Gegeben ist ein nichtdeterministischer endlicher Automat N. Gesucht ist ein deterministischer endlicher Automat D, der dieselbe Sprache erkennt, d.h. für den gilt: L(D) = L(N).
Deterministischer endlicher Automat
Die Übergangsrelation eines nichtdeterministischen endlichen Automaten kann so beschaffen sein, dass manche Zustände mehrere Folgezustände unter einem bestimmten Eingabezeichen a ∈ A haben, manche Zustände dagegen gar keinen Folgezustand unter einem bestimmten Eingabezeichen a ∈ A. Bei einem deterministischen endlichen Automaten ist dies nicht erlaubt. Beim deterministischen endlichen Automaten hat jeder Zustand unter jedem Eingabezeichen a ∈ A genau einen Folgezustand. Die Übergangsrelation eines deterministischen endlichen Automaten ist eindeutig und total definiert – und damit eine Übergangsfunktion:
d : Z × A → Z
Ein deterministischer endlicher Automat ist somit nicht das Gegenteil, sondern ein Spezialfall eines nichtdeterministischen endlichen Automaten.
Beispiel: Der in Bild 1 dargestellte Automat ist (echt) nichtdeterministisch, denn der Zustand 0 hat unter dem Eingabezeichen a zwei Folgezustände, nämlich 0 und 1. Außerdem hat der Zustand 1 unter dem Eingabezeichen a keinen Folgezustand. Der Zustand 2 hat weder unter a noch unter b einen Folgezustand.

Bild 1: Nichtdeterministischer endlicher Automat N
Die Übergangsfunktion eines deterministischen endlichen Automaten ist nur auf Z × A definiert, daher sind in einem deterministischen endlichen Automaten keine Epsilon-Übergänge erlaubt.
Teilmengenkonstruktion
Aus jedem nichtdeterministischen endlichen Automaten lässt sich ein deterministischer endlicher Automat konstruieren. Die Idee der Konstruktion besteht darin, während der Simulation des nichtdeterministischen endlichen Automaten sozusagen "Momentaufnahmen" zu machen. Diese Momentaufnahmen unterscheiden sich dadurch, dass auf ihnen unterschiedliche Zustände markiert sind. Die Menge dieser unterschiedlichen Momentaufnahmen bildet die Zustandsmenge des deterministischen endlichen Automaten (Bild 2).
Oder genauer ausgedrückt, diejenigen Teilmengen der Zustandsmenge des nichtdeterministischen endlichen Automaten, die während der Simulation jeweils markiert sein können, werden sozusagen als "Superzustände" aufgefasst und zu den Zuständen des deterministischen endlichen Automaten erklärt.
Die Zustände des deterministischen endlichen Automaten sind also Teilmengen der Zustandsmenge des nichtdeterministischen endlichen Automaten, daher wird das Verfahren als Teilmengenkonstruktion bezeichnet.
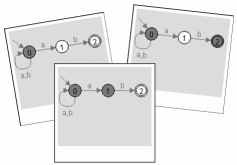
Bild 2: "Momentaufnahmen" bei der Simulation eines nichtdeterministischen endlichen Automaten
Die folgende Simulation des oben angegebenen nichtdeterministischen endlichen Automaten zeigt, dass die Teilmengen {0}, {0, 1} und {0, 2} markiert sein können; der Automat befindet sich also sozusagen jeweils in einem dieser drei Superzustände:
(Java-Applet zur Simulation eines nichtdeterministischen endlichen Automaten)
Verfahren
Mit dem folgenden Verfahren wird ein nichtdeterministischer endlicher Automat N in einen deterministischen endlichen Automaten D umgeformt. Als Beispiel zur Veranschaulichung dient der in Bild 1 gezeigte nichtdeterministische endliche Automat, der die reguläre Sprache L = (a|b)*ab erkennt.
Das hier beschriebene Verfahren geht von einem nichtdeterministischen endlichen Automaten ohne Epsilon-Übergänge aus; es lässt sich aber für nichtdeterministische endliche Automaten mit Epsilon-Übergängen anpassen (siehe Aufgabe 2).
Teilmengenkonstruktion
- Zustandsmenge des zu konstruierenden deterministischen endlichen Automaten D ist zunächst die Potenzmenge
 (Z) der Zustandsmenge Z des nichtdeterministischen endlichen Automaten N, d.h. die Menge aller Teilmengen von Z. Es wird sich zeigen, dass diese Zustände im Allgemeinen nicht alle gebraucht werden, etliche können möglicherweise später wieder entfallen.
(Z) der Zustandsmenge Z des nichtdeterministischen endlichen Automaten N, d.h. die Menge aller Teilmengen von Z. Es wird sich zeigen, dass diese Zustände im Allgemeinen nicht alle gebraucht werden, etliche können möglicherweise später wieder entfallen.
- Startzustand von D ist die Teilmenge {q}, wobei q der Startzustand von N ist.
- Endzustände sind alle Teilmengen T mit T ∩ F ≠ ∅, wobei F die Menge der Endzustände von N ist. D.h. eine Teilmenge T ist Endzustand von D, wenn sie einen Endzustand von N enthält.
Bild 3 zeigt die Menge der Zustände des deterministischen endlichen Automaten D. Die Teilmenge {0} ist der Startzustand, die Teilmengen {2}, {0, 2}, {1, 2} und {0, 1, 2} sind Endzustände, weil sie den Endzustand 2 von N enthalten.

Bild 3: Zustände des zu konstruierenden deterministischen endlichen Automaten D
- Die Übergangsfunktion des deterministischen endlichen Automaten D wird folgendermaßen aus der Übergangsrelation d des nichtdeterministischen endlichen Automaten N konstruiert:
Folgezustand T ' eines Zustands T von D unter einem Eingabezeichen a ∈ A ist die Teilmenge
T ' = { s' | ∃ s ∈ T : (s, a, s') ∈ d }.
T ' besteht also aus den Folgezuständen aller Zustände s ∈ T unter dem Eingabezeichen a in N.
Als erstes werden die Folgezustände des Startzustands T = {q} berechnet, dann deren Folgezustände usw., solange, bis keine weiteren Zustandsübergänge mehr hinzu kommen. Es zeigt sich, dass meist gar nicht alle Zustände vom Startzustand aus erreichbar sind; diese Zustände können entfallen, die Zustandsübergänge zwischen ihnen brauchen nicht berechnet zu werden.
In Bild 4 ist zu sehen, dass in D die Teilmenge T ' = {0, 1} der Folgezustand von T = {0} unter dem Eingabezeichen a ist, weil in N die Zustände 0 und 1 Folgezustände von 0 unter dem Eingabezeichen a sind.
Der Folgezustand von T = {0, 1} unter dem Eingabezeichen b ist T ' = {0, 2}, denn in N ist 0 Folgezustand von 0 unter b und 2 ist Folgezustand von 1 unter b.
Entsprechend ergeben sich die anderen in Bild 4 eingezeichneten Zustandsübergänge. Die weiteren Zustandsübergänge für die Zustände ∅, {1}, {2}, {1, 2} und {0, 1, 2} brauchen nicht berechnet zu werden, da diese Zustände vom Startzustand {0} aus nicht erreichbar sind.

Bild 4: Konstruktion der Übergangsrelation des deterministischen endlichen Automaten D
- Überflüssige Zustände, also Zustände von D, die vom Startzustand {q} aus nicht erreichbar sind, werden entfernt.
Bild 5 zeigt den deterministischen endlichen Automaten D ohne diese überflüssigen Zustände.

Bild 5: Deterministischer endlicher Automat D ohne überflüssige Zustände
Wenn es im Zustandsgraphen von N einen Pfad vom Startzustand zu einem Endzustand gibt, der mit w beschriftet ist, so gibt es aufgrund der Konstruktion auch in D einen Pfad vom Startzustand zu einem Endzustand, der mit w beschriftet ist. Umgekehrt gilt dasselbe. Die beiden Automaten erkennen also dieselbe Sprache, d.h. es ist L(D) = L(N).
Ergebnis
Die eben gezeigte Konstruktion eines deterministischen endlichen Automaten aus einem nichtdeterministischen endlichen Automaten bildet die Grundlage für folgenden Satz.
Satz: Zu jedem nichtdeterministischen endlichen Automaten N gibt es einen deterministischen endlichen Automaten D, der dieselbe Sprache erkennt, und umgekehrt.
Beweis:
| N → D: | D wird durch die Teilmengenkonstruktion aus N erzeugt | |
| D → N: | N = D, da ein deterministischer endlicher Automat ein Spezialfall eines nichtdeterministischen endlichen Automaten ist. |
Die regulären Sprachen werden also von den nichtdeterministischen und den deterministischen endlichen Automaten erkannt.
Aufgaben
Aufgabe 1: Gegeben sei der folgende nichtdeterministische endliche Automat N (Bild 6). Erzeugen Sie aus N mit Hilfe der Teilmengenkonstruktion einen deterministischen endlichen Automaten D, der dieselbe Sprache erkennt.

Bild 6: Nichtdeterministischer endlicher Automat N
Aufgabe 2: Formulieren Sie ein Verfahren, das einen deterministischen endlichen Automaten aus einem nichtdeterministischen endlichen Automaten mit Epsilon-Übergängen konstruiert.
Hinweis: Benutzen Sie den Begriff der Epsilon-Hülle bei der Angabe der Konstruktionsschritte.
Weiter mit: [Komplexität deterministischer endl. Automaten] [Pumping Lemma] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 08.06.2007 Updated: 16.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden