Theoretische Informatik
Komplexität deterministischer endlicher Automaten
Wir haben gesehen, dass nichtdeterministische endliche Automaten und deterministische endliche Automaten dieselbe Klasse von Sprachen erkennen, nämlich die regulären Sprachen. Wozu betrachten wir dann überhaupt nichtdeterministische endliche Automaten? Sind nicht deterministische endliche Automaten viel leichter zu verstehen, zu konstruieren und zu implementieren?
Zunächst einmal ist das Konzept des Nichtdeterminismus ein zentrales Konzept in der theoretischen Informatik, und es lässt sich anhand des endlichen Automaten am leichtesten verstehen. Zudem sind nichtdeterministische endliche Automaten meist nicht schwerer, sondern erheblich leichter zu konstruieren als deterministische endliche Automaten. Andererseits ist richtig, dass deterministische endliche Automaten leichter zu implementieren sind – Nichtdeterminismus als gedankliches Konzept lässt sich nicht implementieren, sondern nur simulieren.
Aber es zeigt sich, und darauf wollen wir im Folgenden eingehen, dass deterministische endliche Automaten so komplex werden können, dass auch sie praktisch nicht implementiert werden können (jedenfalls nicht in Form einer Zustandsübergangstabelle). Ein äquivalenter nichtdeterministischer Automat kann dagegen sehr einfach aufgebaut sein und effizient simuliert werden.
Komplexität
Die Anzahl der Zustände eines endlichen Automaten ist ein Maß für seine Komplexität. Der folgende Satz sagt aus, dass es bezüglich der Komplexität dramatische Unterschiede geben kann zwischen einem nichtdeterministischen endlichen Automaten und jedem äquivalenten deterministischen endlichen Automaten.
Satz: Es gibt eine Sprache Lk, die von einem nichtdeterministischen endlichen Automaten mit k+1 Zuständen erkannt wird, aber von keinem deterministischen endlichen Automaten mit weniger als 2k Zuständen.
Konkret bedeutet die Aussage dieses Satzes, dass beispielsweise die Sprache Lk für k = 100 von einem nichtdeterministischen endlichen Automaten mit 101 Zuständen erkannt wird. Die Sprache wird aber von keinem deterministischen endlichen Automaten erkannt, der nicht mindestens 2100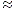 
1030 Zustände hat; entsprechend viele Zeilen hat seine Zustandsübergangstabelle.
Im folgenden Beweis bezeichnet d* die auf Wörter erweiterte Übergangsrelation; entsprechend bezeichnet d*(s, w) den Zustand, den der deterministische Automat erreicht, wenn er ausgehend von einem Zustand s ein Wort w abarbeitet.
Beweis: Sei A = {a, b} und sei Lk die Sprache aller Wörter über A, deren k-letztes Zeichen ein a ist:
Lk = { x ∈ A* | x = x0 ... xn-1, n ≥ k, xn-k = a }
Angenommen, es gibt einen deterministischen endlichen Automaten D = (Z, A, d, q, F) mit weniger als 2k Zuständen, der Lk erkennt.
Weil der Automat D weniger als 2k Zustände hat, kann er nicht alle 2k möglichen Wörter der Länge k über A unterscheiden. D.h. es gibt Wörter u, v ∈ Ak mit u ≠ v, aber d*(q, u) = d*(q, v). Der Automat gerät also bei Abarbeitung von u bzw. von v in denselben Zustand.
Da u ≠ v, gibt es eine Position i, an der sich u und v unterscheiden, also etwa ui = a und vi = b.
Wir hängen nun noch ein Wort w der Länge i an u bzw. v an, bilden also die Wörter
u' = uw und
v' = vw,
wobei |w| = i. Auf diese Weise wird ui = a bzw. vi = b jeweils zum k-letzten Zeichen von u' bzw. v'. Somit gilt u' ∈ Lk, aber v' ∉ Lk.
Wenn nun der Automat D das Wort u' abarbeitet, so gilt
d*(q, u') = d*(d*(q, u), w) = d*(d*(q, v), w) = d*(q, v').
Dies bedeutet, dass der Automat bei Abarbeitung von u' bzw. von v' in denselben Zustand gerät. Je nach dem, ob dieser Zustand ein Endzustand ist oder nicht, erkennt der Automat fälschlicherweise entweder v' oder er erkennt u' nicht. Es ergibt sich somit ein Widerspruch zur Annahme, dass D die Sprache Lk erkennt. Also ist die Annahme falsch. D.h. jeder deterministische endliche Automat, der Lk erkennt, hat mindestens 2k Zustände.
Aufgaben
Aufgabe 1: Geben Sie einen nichtdeterministischen endlichen Automaten mit k+1 Zuständen an, der die Sprache Lk aller Wörter über {a, b}, deren k-letztes Zeichen ein a ist, erkennt.
Weiter mit: [Abgeschlossenheitseigenschaften regulärer Sprachen] [Pumping-Lemma] [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 10.12.2012 Updated: 16.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden