Theoretische Informatik
Pumping-Lemma für reguläre Sprachen
Um zu zeigen, dass eine Sprache regulär ist, genügt es, einen regulären Ausdruck anzugeben, der sie erzeugt, oder einen endlichen Automaten anzugeben, der sie erkennt, oder eine rechtslineare Grammatik anzugeben, die sie erzeugt.
Wie aber kann man zeigen, dass eine Sprache nicht regulär ist? Hierzu ist der folgende Satz ein wichtiges Hilfsmittel.
Pumping-Lemma
Satz: (Pumping-Lemma)
Sei A ein Alphabet und L ⊆ A* eine reguläre Sprache. Dann lassen sich alle Wörter x ∈ L ab einer gewissen Länge |x| ≥ p (der Pumping-Länge) zerlegen in
x = uvw mit u, v, w ∈ A*
mit
0 < |v| ≤ |uv| ≤ p ,
sodass gilt
uvkw ∈ L für alle k ∈ ℕ0.
Alle Wörter x ab einer gewissen Länge p (der Pumping-Länge) enthalten also ein nichtleeres Teilwort v, mit dem sich das Wort x "aufpumpen" lässt – daher die Bezeichnung Pumping-Lemma.
Beweis:
Die Sprache L ist regulär, also gibt es einen deterministischen endlichen Automaten, der L erkennt. Sei p = |Z|, die Anzahl der Zustände dieses Automaten. Wenn der Automat ein Wort x = x0 ... xm-1 der Länge m ≥ p erkennt, so gibt es einen mit x markierten Pfad vom Startzustand q = s0 zu einem Endzustand sm ∈ F im Zustandsgraphen des Automaten. Dieser Pfad enthält m+1 > p Zustände. Diese können nicht alle verschieden sein, sondern es muss einen Index j ≤ p geben, derart dass s0, ..., sj-1 verschieden sind und sj = si für ein i ∈ {0, ..., j-1}. Der Automat gelangt also mit x0 ... xi-1 ausgehend von Startzustand s0 in den Zustand si, von dort mit xi ... xj-1 in den Zustand sj = si, und von dort mit xj ... xm-1 in den Zustand sm. Der Pfad von s0 nach sm im Zustandsgraphen enthält also einen Zyklus, der mit xi ... xj-1 markiert ist. Dieser Zyklus kann mehrfach oder auch gar nicht durchlaufen werden (Bild 1).
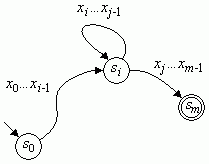
Bild 1: Zyklus im Zustandsgraphen
Somit lässt sich x = x0 ... xm-1 darstellen als
x = uvw mit
u = x0 ... xi-1
v = xi ... xj-1
w = xj ... xm-1
und es gilt
0 < |v|, da i < j,
|uv| ≤ p, da j ≤ p
sowie
uvkw ∈ L für alle k ∈ ℕ0.
Anwendung
Typischerweise wird das Pumping-Lemma angewendet, um durch einen Widerspruchsbeweis zu zeigen, dass eine Sprache L nicht regulär ist.
Satz: Die Sprache L = { anbn | n ∈ ℕ } ist nicht regulär.
Beweis: Angenommen, L ist regulär. Dann gilt das Pumping-Lemma. Sei nun p die Pumping-Länge und sei x = apbp. Dann gilt |x| ≥ p und x lässt sich somit darstellen als x = uvw mit
0 < |v| ≤ |uv| ≤ p
Da |uv| ≤ p, besteht uv nur aus a's, und damit besteht auch v nur aus a's. Sei r die Länge von v; es gilt r > 0. Dann ist nach dem Pumping-Lemma auch uv2w = ap+rbp ∈ L, im Widerspruch zur Definition von L. Also ist die Annahme falsch, L ist also nicht regulär.
Die Anwendung des Pumping-Lemmas verläuft immer nach diesem Schema. Wir nehmen an, dass L regulär ist. Dann gilt das Pumping-Lemma, und es gibt somit eine Pumping-Länge p.
Jetzt müssen wir nur ein einziges Wort x ∈ L finden, das lang genug ist, d.h. mit |x| ≥ p, und ein Anfangswort uv von x, das kurz genug ist, d.h. mit |uv| ≤ p, und das so beschaffen ist, dass wir in uv einen beliebigen Teil v "aufpumpen" können, um Wörter zu erhalten, die nicht in L liegen. Damit erhalten wir einen Widerspruch zur Annahme, dass L regulär ist.
In obigem Beweis haben wir dafür gesorgt, dass uv nur aus a's besteht. Somit besteht auch das Teilwort v nur aus a's, ganz gleich, welchen Teil von uv es einnimmt. Wird nun v "aufgepumpt", so entstehen Wörter mit mehr a's als b's, also Wörter, die nicht in L liegen. Damit kann L nicht regulär sein.
Aufgaben
Aufgabe 1:
Sei L die Sprache aller Wörter über dem Alphabet A = {a, b}, die aus gleich vielen a's und b's bestehen, d.h.
L = { w ∈ {a, b}* | |w|a = |w|b }
Die Notation |w|a bezeichnet die Anzahl der a's im Wort x.
Zeigen Sie durch Anwendung des Pumping-Lemmas: L ist nicht regulär.
Hinweis: Beginnen Sie Ihren Beweis so: "Angenommen, die Sprache L ist regulär. Dann gilt das Pumping-Lemma. Sei p die Pumping-Länge und sei x = ... "
Aufgabe 2:
Sei L die Sprache der Palindrome1) gerader Länge über dem Alphabet A = {a, b}, d.h.
L = { wwR | w ∈ {a, b}*, wR ist das Spiegelbild von w }
Zeigen Sie durch Anwendung des Pumping-Lemmas: L ist nicht regulär.
Hinweis: Beginnen Sie Ihren Beweis so: "Angenommen, die Sprache L ist regulär. Dann gilt das Pumping-Lemma. Sei p die Pumping-Länge und sei x = ... "
1) Ein Palindrom ist ein Wort, das man vorwärts und rückwärts lesen kann, wie z.B. otto.
Weiter mit: [Grammatik] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 26.01.2007 Updated: 16.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden