Theoretische Informatik
Konstruktion eines nichtdeterministischen endlichen Automaten
aus einem regulären Ausdruck (top-down)
Gegeben ist ein regulärer Ausdruck R und ein Wort w. Es stellt sich die Frage, ob w von R erzeugt wird, d.h. ob w in der von R erzeugten regulären Sprache L(R) enthalten ist.
Diese Frage ist auf direktem Wege im Allgemeinen schwer zu beantworten. Meist ist es nicht offensichtlich, ob es eine Möglichkeit gibt, das Wort w aus dem regulären Ausdruck R zu erzeugen. Eine systematische Methode zur Entscheidung der Frage geht den Umweg über einen nichtdeterministischen endlichen Automaten.
Hierzu wird aus dem regulären Ausdruck R ein nichtdeterministischer endlicher Automat N konstruiert. Der Automat wird so konstruiert, dass er genau alle jene Wörter akzeptiert, die zu L(R) gehören.
Satz: Zu jedem regulären Ausdruck R gibt es einen nichtdeterministischen endlichen Automaten N, der die von R erzeugte reguläre Sprache L(R) erkennt.
Zum Beweis des Satzes wird im Folgenden ein Verfahren angegeben, mit dem der Zustandsgraph des entsprechenden Automaten rekursiv aus dem gegebenen regulären Ausdruck konstruiert wird. Hierbei wird der reguläre Ausdruck top-down in immer kleinere reguläre Ausdrücke zerlegt und parallel dazu der Zustandsgraph des Automaten konstruiert.
Ein anderes Verfahren baut den regulären Ausdruck bottom-up aus Teilausdrücken auf und konstruiert parallel dazu den Zustandsgraphen des Automaten. Das entsprechende Verfahren ist in Konstruktion eines nichtdeterministischen endlichen Automaten (bottom-up) beschrieben.
Verfahren
Als erstes wird ein Zustandsgraph mit einem Startzustand und einem Endzustand erzeugt. Startzustand und Endzustand sind durch einen Zustandsübergang miteinander verbunden, der mit dem regulären Ausdruck R beschriftet ist (Bild 1). Dieser Zustandsgraph beschreibt offenbar das Verhalten eines Automaten, der die regulären Sprache L(R) erkennt – allerdings nur ganz grob, die inneren Zustände des Automaten bleiben zunächst unbestimmt.
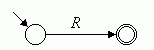
Bild 1: Anfangssituation
Durch Zerlegung dieses Zustandsübergangs werden nach und nach die inneren Zustände des Automaten erzeugt. Dabei gelten folgende Regeln:
- Jeder Zustandsübergang, der mit S | T beschriftet ist, wird in zwei parallele Zustandsübergänge zerlegt, die mit S bzw. mit T beschriftet sind (Bild 2a).
- Jeder Zustandsübergang, der mit ST beschriftet ist, wird in zwei aufeinander folgende Zustandsübergänge zerlegt, die mit S bzw. mit T beschriftet sind (Bild 2b).
- Jeder Zustandsübergang, der mit S* beschriftet ist, wird wie in Bild 2c gezeigt zerlegt.
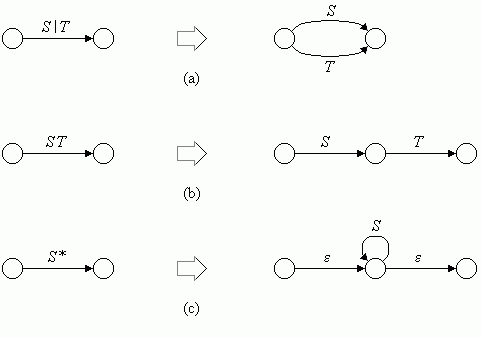
Bild 2: Zerlegen der Zustandsübergänge S|T, ST und S*
Am Ende des Verfahrens werden parallele Zustandsübergänge, die mit einzelnen Zeichen beschriftet sind, zu einem Zustandsübergang zusammengefasst, sodass jeder Zustandsübergang mit einer Elementarsprache beschriftet ist. Das Ergebnis ist der Zustandsgraph des gesuchten nichtdeterministischen endlichen Automaten.
Der erzeugte Automat enthält im Allgemeinen Epsilon-Übergänge. Durch anschließende Beseitigung dieser Epsilon-Übergänge mithilfe des bekannten Verfahrens lässt sich auch ein nichtdeterministischer endlicher Automat ohne Epsilon-Übergänge erzeugen.
Beispiel
Als Beispiel zur Veranschaulichung dient der reguläre Ausdruck
R = a(a | b)*a | a
In Bild 3 sind die einzelnen Schritte des Verfahrens dargestellt.
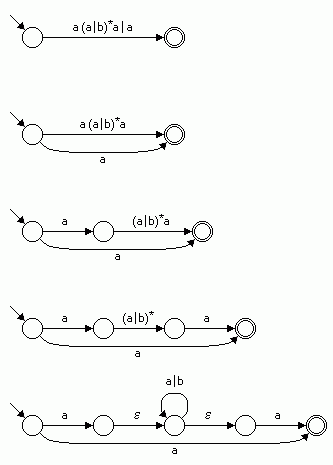
Bild 3: Konstruktion am Beispiel des regulären Ausdrucks a(a | b)*a | a
Aufgabe
Aufgabe 1: Konstruieren Sie nach dem angegebenen Verfahren einen nichtdeterministischen endlichen Automaten N aus dem regulären Ausdruck
R = (a | ba | bba)*(ε | b | bb)
über dem Alphabet A = {a, b}. Die erzeugte bzw. erkannte Sprache umfasst alle Wörter über A, die höchstens zwei b's hintereinander enthalten.
Weiter: [Konstruktion eines regulären Ausdrucks aus einem endlichen Automaten] [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 26.01.2003 Updated: 16.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden