Theoretische Informatik
Konstruktion eines regulären Ausdrucks
aus einem nichtdeterministischen endlichen Automaten
Gegeben ist ein nichtdeterministischer endlicher Automat N. Gesucht ist ein regulärer Ausdruck R, der genau die Sprache erzeugt, die der Automat N erkennt, d.h. L(R) = L(N).
Satz: Zu jedem nichtdeterministischen endlichen Automaten N gibt es einen regulären Ausdruck R, der die von N erkannte Sprache L(N) erzeugt.
Zum Beweis des Satzes wird ein Verfahren angegeben, das einen beliebigen nichtdeterministischen endlichen Automaten in einen regulären Ausdruck umformt. Als Beispiel zur Veranschaulichung dient der in Bild 1 gezeigte nichtdeterministische endliche Automat N.

Bild 1: Umzuformender nichtdeterministischer endlicher Automat N
Das Verfahren ist die Umkehrung des Verfahrens zur Konstruktion eines nichtdeterministischen endlichen Automaten aus einem regulären Ausdruck.
Verfahren
In dem Verfahren werden aus dem Zustandsgraphen des Automaten nach und nach die inneren Zustände entfernt und dafür die Kanten mit zunehmend komplexeren regulären Ausdrücken beschriftet. Zum Schluss besteht der Zustandsgraph nur noch aus Startzustand und Endzustand und einem Zustandsübergang, der mit dem gesuchten regulären Ausdruck beschriftet ist.
Zunächst wird ein neuer Startzustand eingeführt und durch einen Epsilon-Übergang mit dem ursprünglichen Startzustand verbunden. Ferner wird ein neuer Endzustand eingeführt. Alle bisherigen Endzustände verlieren ihre Endzustandseigenschaft; sie werden mit dem neuen Endzustand durch Epsilon-Übergänge verbunden (Bild 2).

Bild 2: Zustandsgraph des Automaten N mit neuem Start- und neuem Endzustand
Außer dem Startzustand und dem Endzustand werden nun schrittweise alle Zustände nach folgenden Regeln entfernt.
Wenn ein Zustand s entfernt wird, so wird jeder Kantenzug (r, s)(s, t) mit r, t ≠ s durch eine Kante (r, t) ersetzt. Sind hierbei die Kanten (r, s) und (s, t) mit den regulären Ausdrücken S bzw. T beschriftet, so wird die neue Kante (r, t)
- mit dem regulären Ausdruck ST beschriftet, wenn keine Kante (s, s) vorhanden ist (Bild 3),
- mit dem regulären Ausdruck SX*T beschriftet, wenn eine Schlinge (s, s) vorhanden ist, die mit dem regulären Ausdruck X beschriftet ist (Bild 4).

Bild 3: Entfernen eines Zustandes

Bild 4: Entfernen eines Zustandes mit Schlinge
Ist nach dem Entfernen eines Zustands eine Doppelkante zwischen zwei Zuständen vorhanden, so wird diese durch eine einfache Kante ersetzt. Die Beschriftung dieser neuen Kante ist S | T, wenn S bzw. T die Beschriftungen der Doppelkante waren (Bild 5).

Bild 5: Ersetzen einer Doppelkante
Beispiel
Folgendes Bild 6 zeigt die Anwendung des Verfahrens auf den als Beispiel angegebenen Automaten. Das Ergebnis ist ein Zustandsgraph, dessen einziger Zustandsübergang mit dem gesuchten regulären Ausdruck beschriftet ist.
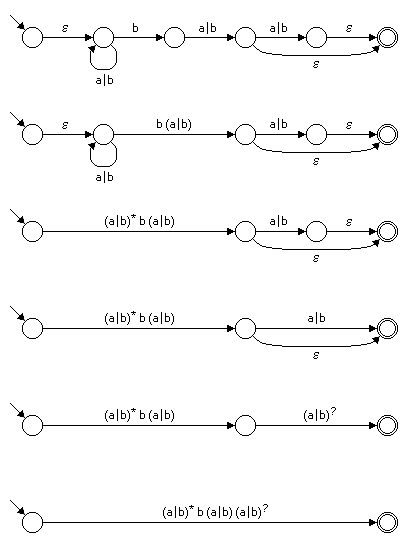
Bild 6: Schrittweises Entfernen von Zuständen
Aufgaben
Aufgabe 1: Gegeben ist folgender (deterministische) endliche Automat, der alle Wörter über dem Alphabet A = {a, b} erkennt, die eine gerade Anzahl von b's enthalten.
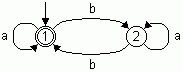
Erzeugen Sie nach dem angegebenen Verfahren aus dem Automaten einen regulären Ausdruck.
Aufgabe 2: Gegeben ist folgender (deterministische) endliche Automat, der alle Wörter über dem Alphabet A = {a, b} erkennt, die eine gerade Anzahl von a's und von b's enthalten.
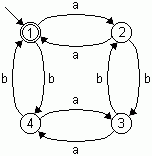
Erzeugen Sie nach dem angegebenen Verfahren aus dem Automaten einen regulären Ausdruck.
Weiter mit: [Konstruktion eines deterministischen aus einem nichtdet. endl. Automaten] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 19.04.2007 Updated: 25.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden