Theoretische Informatik
Äquivalenz von nichtdeterministischen endlichen Automaten ohne und mit Epsilon-Übergängen
Es stellt sich die Frage, ob nichtdeterministische endliche Automaten mit Epsilon-Übergängen mehr können als normale nichtdeterministische endliche Automaten. Gibt es also eine Sprache, die von einem nichtdeterministischen endlichen Automaten mit Epsilon-Übergängen erkannt wird, aber nicht von einem normalen nichtdeterministischen endlichen Automaten? Die Antwort ist nein.
Konstruktion
Satz: Zu jedem nichtdeterministischen endlichen Automaten mit Epsilon-Übergängen gibt es einen nichtdeterministischen endlichen Automaten ohne Epsilon-Übergänge, der dieselbe Sprache erkennt.
Beweis: Wir formen einen gegebenen nichtdeterministischen endlichen Automaten mit Epsilon-Übergängen in einen normalen nichtdeterministischen endlichen Automaten um, indem wir alle Epsilon-Übergänge beseitigen, ohne dass sich die erkannte Sprache ändert.
Sei N = (Z, A, d, q, F) der gegebene nichtdeterministische endliche Automat mit Epsilon-Übergängen. Wir konstruieren hieraus einen normalen nichtdeterministischen endlichen Automaten N' in folgender Weise.
Zustandsmenge Z, Eingabealphabet A und Startzustand q werden von N übernommen; neu erzeugt werden die Übergangsrelation d' und die Menge der Endzustände F'.
Die Übergangsrelation d' besteht jeweils aus Zustandsübergängen (r, a, t) mit a ∈ A, falls es in N Zustände s, s' gibt mit
(r, ε, s) ∈ d* ∧ (s, a, s') ∈ d ∧ (s', ε, t) ∈ d*
Die neuen Zustandsübergänge in d' ergeben sich also aus den Nicht-Epsilon-Übergängen aus d mit vor- und nachgeschalteten Ketten von Epsilon-Übergängen.
Diese Ketten von Epsilon-Übergängen dürfen auch die Länge 0 haben, d.h. zu den Zustandsübergängen in d' gehören insbesondere auch die Nicht-Epsilon-Übergänge (r, a, t) von d, denn es gilt mit s = r und s' = t:
(r, ε, r) ∈ d* ∧ (r, a, t) ∈ d ∧ (t, ε, t) ∈ d*
Anders ausgedrückt enthält die Übergangsrelation d' alle Elemente der auf Wörter erweiterten Übergangsrelation d*, bei denen das jeweilige Wort die Länge 1 hat:
d' = { (r, w, t) ∈ d* | |w| = 1 }
Somit enthält d' keine Epsilon-Übergänge, und wir haben d' gerade so konstruiert, dass wenn wir im Zustandsgraphen von N mit dem Zeichen a vom Zustand r zum Zustand t kommen, dasselbe auch in N' gilt. Kommen wir umgekehrt im Zustandsgraphen von N' mit dem Zeichen a von r nach t, so auch in N. Für nichtleere Wörter w ∈ A+ gilt daher: N' erkennt jedes Wort, das N erkennt, und umgekehrt.
Die von N und N' erkannten Sprachen sind also gleich, bis möglicherweise auf das Wort ε.
In N können wir möglicherweise vom Startzustand q mit dem Wort ε zu einem Endzustand t ≠ q gelangen, aber in N' natürlich nicht, weil N' keine Epsilon-Übergänge hat. Damit ε auch von N' erkannt wird, muss in diesem Fall der Startzustand q' auch zum Endzustand gemacht werden.
| F' = |  |
|
Beispiel
Beispiel: Gegeben sei der folgende nichtdeterministische endliche Automat N mit Epsilon-Übergängen (Bild 1a). Aus N wird ein äquivalenter nichtdeterministischer endlicher Automat N' ohne Epsilon-Übergänge konstruiert (Bild 1b).
Zunächst enthält die Übergangsrelation von N alle Nicht-Epsilon-Übergänge von N':
| (1, a, 1) | weil (1, ε, 1) ∈ d* | ∧ | (1, a, 1) ∈ d | ∧ | (1, ε, 1) ∈ d* | |
| (2, b, 3) | weil (2, ε, 2) ∈ d* | ∧ | (2, b, 3) ∈ d | ∧ | (3, ε, 3) ∈ d* |
Hinzu kommen die folgenden weiteren Zustandsübergänge:
| (0, a, 1) | weil (0, ε, 1) ∈ d* | ∧ | (1, a, 1) ∈ d | ∧ | (1, ε, 1) ∈ d* | |
| (1, a, 2) | weil (1, ε, 1) ∈ d* | ∧ | (1, a, 1) ∈ d | ∧ | (1, ε, 2) ∈ d* | |
| (1, b, 3) | weil (1, ε, 2) ∈ d* | ∧ | (2, b, 3) ∈ d | ∧ | (3, ε, 3) ∈ d* | |
| (0, a, 2) | weil (0, ε, 1) ∈ d* | ∧ | (1, a, 1) ∈ d | ∧ | (1, ε, 2) ∈ d* | |
| (0, b, 3) | weil (0, ε, 2) ∈ d* | ∧ | (2, b, 3) ∈ d | ∧ | (3, ε, 3) ∈ d* |
Außerdem muss der Startzustand 0 zum Endzustand gemacht werden, weil vom Zustand 0 aus der Endzustand 2 über Epsilon-Übergänge erreicht werden kann.
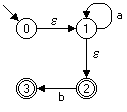
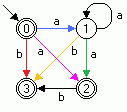
Bild 1: Nichtdeterministische endliche Automaten N mit Epsilon-Übergängen (a) und N' ohne Epsilon-Übergänge (b)
Weiter mit: [Konstruktion eines nichtdet. endl. Automaten aus einem regulären Ausdruck] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 16.10.2010 Updated: 16.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden