Theoretische Informatik
Konstruktion eines nichtdeterministischen endlichen Automaten
aus einem regulären Ausdruck (bottom-up)
Zu jedem regulären Ausdruck R gibt es einen nichtdeterministischen endlichen Automaten N, der die von R erzeugte reguläre Sprache L(R) erkennt.
Der nichtdeterministische endliche Automat N lässt sich entweder top-down oder bottom-up induktiv über den Aufbau von R konstruieren. Das Top-Down-Verfahren beginnt mit einem erweiterten Automaten mit zwei Zuständen, dessen einziger Zustandsübergang mit R markiert ist, und zerlegt diesen nach und nach. Das Bottom-Up-Verfahren beginnt mit elementaren Automaten für die Elementarsprachen, die in R enthalten sind, und setzt diese nach und nach zusammen [AHU 74]. Dieses Verfahren ist im Folgenden dargestellt. Das andere Verfahren ist in Konstruktion eines nichtdeterministischen endlichen Automaten (top-down) beschrieben.
Verfahren
Die elementaren Automaten für die Elementarsprachen {a} ⊆ A1 und für die leere Menge ∅ sind in Bild 1 dargestellt:
| R = a mit {a} ⊆ A1 | NR = | 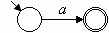 | |
| R = ∅ | NR = | 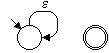 |
Bild 1: Elementare Automaten für die regulären Ausdrücke R = a und R = ∅
Wenn also der reguläre Ausdruck R nur aus der Elementarsprache {a} besteht, dann ist der zugehörigen Automat N sehr einfach: Er hat einen Startzustand, einen Endzustand und einen Zustandsübergang, nämlich vom Startzustand zum Endzustand unter dem Zeichen a. Der Automat erkennt dann genau die Sprache {a}.
Wenn der reguläre Ausdruck R die leere Menge ist, besteht der zugehörige Automat aus Start- und Endzustand, die jedoch durch keinen Zustandsübergang verbunden sind. Daher ist der Endzustand nicht erreichbar. Der Automat kann also nie in den Endzustand gelangen; die erkannte Sprache ist daher die leere Menge.1)
Seien nun S und T reguläre Ausdrücke und NS und NT die zugehörigen Automaten, wie in Bild 2 schematisch dargestellt.

Bild 2: Schematische Darstellung der Automaten NS und NT
Dann werden die Automaten für S | T, ST und S* wie in Bild 3 dargestellt konstruiert:
| R = S | T | NR = | 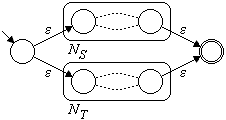 | ||
| R = ST | NR = | 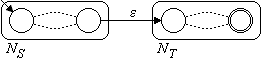 | ||
| R = S* | NR = | 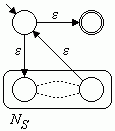 |
Bild 3: Automaten für S | T, ST und S*
Die auf diese Weise konstruierten Automaten enthalten viele Epsilon-Übergänge. Die Anzahl der Zustände ist dadurch größer als eigentlich notwendig. Auf der anderen Seite haben die Automaten jedoch einige Eigenschaften, die für die Implementation vorteilhaft sind:
- Jeder Zustand hat höchstens zwei Folgezustände.
- Hat ein Zustand zwei Folgezustände, so führen ε-Übergänge dorthin.
- Ein Zustand ist genau dann Endzustand, wenn er keinen Folgezustand hat.
- Es gibt genau einen Endzustand.
Beispiel: Folgendes Bild 4 zeigt den nach dieser Methode konstruierten nichtdeterministischen endlichen Automaten N, der zu dem regulären Ausdruck R = (a | b)*a gehört.
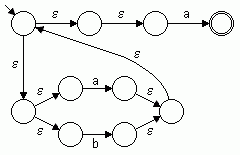
Bild 4: Nichtdeterministischer endlicher Automat für (a | b)*a
Recursive-Descent-Übersetzung von regulären Ausdrücken
Um für einen beliebigen regulären Ausdruck R und ein beliebiges Wort w über einem Alphabet A zu entscheiden, ob w von R erzeugt wird, sind zwei Schritte nötig:
- Konstruktion eines nichtdeterministischen endlichen Automaten N zu dem regulären Ausdruck R
- Simulation des nichtdeterministischen endlichen Automaten N mit dem Eingabewort w
Wenn der Automat das Wort erkennt, wird es von dem regulären Ausdruck erzeugt und sonst nicht.
Es wird jetzt noch ein Verfahren gebraucht, das den Aufbau eines regulären Ausdrucks analysiert und nach der oben beschriebenen Methode den zugehörigen nichtdeterministischen endlichen Automaten konstruiert. In klassischer Weise wird dies von einem Recursive-Descent-Übersetzer geleistet, der einen regulären Ausdruck in den zugehörigen nichtdeterministischen endlichen Automaten übersetzt. Das folgende Bild 5 illustriert diese Vorgehensweise:
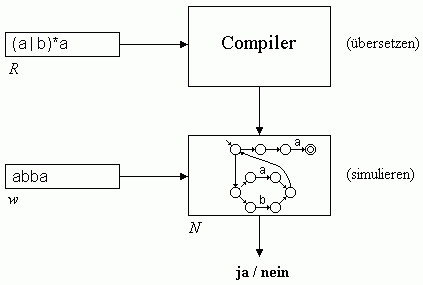
Bild 5: Prüfen, ob das Wort w von dem regulären Ausdruck R erzeugt wird
Visualisierung
In folgendem Applet wird durch Recursive-Descent-Übersetzung aus einem regulären Ausdruck ein nichtdeterministischer endlicher Automat konstruiert, der die zugehörige reguläre Sprache erkennt.
Bei Eingabe eines syntaktisch nicht korrekten regulären Ausdrucks wird eine Fehlermeldung sowie die Position des Fehlers ausgegeben.
Der Automat wird als Zustandsgraph ausgegeben; hierbei stehen Pfeile ohne Markierung für Epsilon-Übergänge.
Das Alphabet besteht hier nur aus den Symbolen a, b, c. Das Zeichen % steht für die leere Menge.
(Java-Applet zur Konstruktion eines nichtdeterministischen endlichen Automaten aus einem regulären Ausdruck)
Literatur
[AHU 74] A.V. Aho, J.E. Hopcroft, J.D. Ullman: The Design and Analysis of Computer Algorithms. Addison-Wesley (1974)
1) Der Epsilon-Übergang ist nötig, damit der Automat die unten angegebenen Bedingungen 3 und 4 erfüllt.
Weiter mit: [Recursive-Descent-Übersetzung], [Übersetzung regulärer Ausdrücke] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 26.01.2003 Updated: 16.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden